一、插值要求和目的
要求
1、 利用Lagrange插值公式
L
n
(
x
)
=
∑
k
=
0
n
(
∏
i
=
0
,
i
≠
k
n
x
−
x
i
x
k
−
x
i
)
y
k
{L_n}(x) = \sum\limits_{k = 0}^n {\left( {\prod\limits_{i = 0,i \ne k}^n {\frac{{x - {x_i}}}{{{x_k} - {x_i}}}} } \right)} {y_k}
Ln(x)=k=0∑n(i=0,i=k∏nxk−xix−xi)yk 编写出插值多项式程序;
2、 给出插值多项式或分段三次插值多项式的表达式;
3、 根据节点选取原则,对问题(2)用三点插值或二点插值,其结果如何;
目的和意义
1、 学会常用的插值方法,求函数的近似表达式,以解决其它实际问题;
2、 明确插值多项式和分段插值多项式各自的优缺点;
3、 熟悉插值方法的程序编制;
4、 如果绘出插值函数的曲线,观察其光滑性。
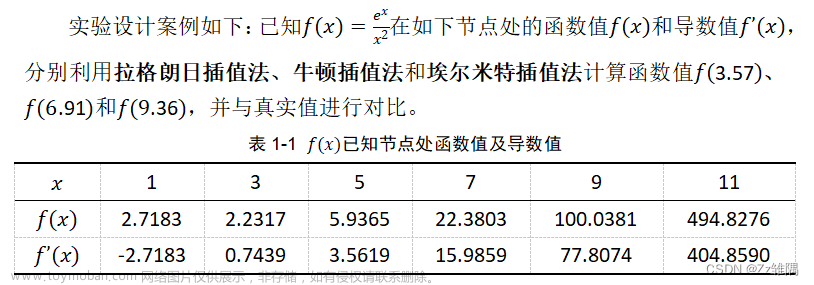
二、题目
对于给定的一元函数
y
=
f
(
x
)
y = f(x)
y=f(x)的n+1个节点值
y
j
=
f
(
x
j
)
,
j
=
0
,
1
,
⋯
,
n
{y_j} = f({x_j}),j = 0,1, \cdots ,n
yj=f(xj),j=0,1,⋯,n。试用Lagrange公式求其插值多项式或分段二次Lagrange插值多项式。
数据如下:
题目(1)
| x j {x_j} xj | 0.4 | 0.55 | 0.65 | 0.80 | 0.95 | 1.05 |
|---|---|---|---|---|---|---|
| y j {y_j} yj | 0.41075 | 0.57815 | 0.69675 | 0.90 | 1.00 | 1.25382 |
求五次Lagrange多项式
L
5
(
x
)
{{\rm{L}}_5}(x)
L5(x),和分段三次插值多项式,计算
f
(
0.596
)
f(0.596)
f(0.596),
f
(
0.99
)
f(0.99)
f(0.99)的值。
(提示:结果为
f
(
0.596
)
≈
0.625732
f(0.596) \approx 0.625732
f(0.596)≈0.625732,
f
(
0.99
)
≈
1.05423
f(0.99) \approx 1.05423
f(0.99)≈1.05423)
题目(2)
| x j {x_j} xj | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|
| y j {y_j} yj | 0.368 | 0.135 | 0.050 | 0.018 | 0.007 | 0.002 | 0.001 |
试构造Lagrange多项式 L 6 ( x ) {{\rm{L}}_6}(x) L6(x),计算的 f ( 1.8 ) f(1.8) f(1.8), f ( 6.15 ) f(6.15) f(6.15)值。(提示:结果为 f ( 1.8 ) ≈ 0.164762 f(1.8) \approx 0.164762 f(1.8)≈0.164762, f ( 6.15 ) ≈ 0.001266 f(6.15) \approx 0.001266 f(6.15)≈0.001266)
三、求解与代码实现
题目(1)
五次拉格朗日:
L
5
(
x
)
=
∑
k
=
0
5
(
∏
i
=
0
,
i
≠
k
5
x
−
x
i
x
k
−
x
i
)
y
k
{L_5}(x) = \sum\limits_{k = 0}^5 {\left( {\prod\limits_{i = 0,i \ne k}^5 {\frac{{x - {x_i}}}{{{x_k} - {x_i}}}} } \right)} {y_k}
L5(x)=k=0∑5(i=0,i=k∏5xk−xix−xi)yk
三次插值多项式:
S
(
x
)
=
y
k
−
1
+
[
y
k
−
y
k
−
1
h
k
−
1
−
h
k
−
1
6
(
2
m
k
−
1
+
m
k
)
]
(
x
−
x
k
−
1
)
+
m
k
−
1
2
(
x
−
x
k
−
1
)
2
+
m
k
−
m
k
−
1
6
h
k
−
1
(
x
−
x
k
=
1
)
2
S(x) = {y_{k - 1}} + [\frac{{{y_k} - {y_{k - 1}}}}{{{h_{k - 1}}}} - \frac{{{h_{k - 1}}}}{6}(2{m_{k - 1}} + {m_k})](x - {x_{k - 1}}) + \frac{{{m_{k - 1}}}}{2}{(x - {x_{k - 1}})^2} + \frac{{{m_k} - {m_{k - 1}}}}{{6{h_{k - 1}}}}{(x - {x_{k = 1}})^2}
S(x)=yk−1+[hk−1yk−yk−1−6hk−1(2mk−1+mk)](x−xk−1)+2mk−1(x−xk−1)2+6hk−1mk−mk−1(x−xk=1)2,
其中:
h
k
=
x
k
+
1
−
x
k
,
m
k
=
S
′
′
(
x
k
)
{h_k} = {x_{k + 1}} - {x_k},{m_k} = S''({x_k})
hk=xk+1−xk,mk=S′′(xk)
lagrange.m
function yh=lagrange(x,y,xh)
n = length(x);
m = length(xh);
x = x(:);
y = y(:);
xh = xh(:);
yh = zeros(m,1);
c1 = ones(1,n-1);
c2 = ones(m,1);
for i=1:n
xp = x([1:i-1 i+1:n]);
yh = yh + y(i) * prod((xh*c1-c2*xp')./(c2*(x(i)*c1-xp')),2);
end
work1.m
x = [0.4, 0.55, 0.65, 0.8, 0.95, 1.05];
y = [0.41075, 0.57815, 0.69675, 0.90, 1.00, 1.25382];
xh = [0.596, 0.99];
lagrange(x, y, xh)
%
MATLAB中的插值函数为interp1,其调用格式为: yi= interp1(x,y,xi,'method')
其中x,y为插值点,yi为在被插值点xi处的插值结果;x,y为向量,
'method'表示采用的插值方法,MATLAB提供的插值方法有几种:
'nearest'是最邻近插值, 'linear'线性插值; 'spline'三次样条插值; 'pchip'立方插值.缺省时表示线性插值
注意:所有的插值方法都要求x是单调的,并且xi不能够超过x的范围。
%}
interp1(x, y, xh, 'spline')
结果截图:

所以可得:
l
a
g
r
a
n
g
e
{
f
(
0.596
)
=
0.6257
f
(
0.99
)
=
1.0542
{\bf{lagrange}}\left\{ \begin{array}{l} f(0.596) = 0.6257\\ f(0.99) = 1.0542 \end{array} \right.
lagrange{f(0.596)=0.6257f(0.99)=1.0542
s
p
l
i
n
e
{
f
(
0.596
)
=
0.6285
f
(
0.99
)
=
1.0677
{\bf{spline}}\left\{ \begin{array}{l} f(0.596) = 0.6285\\ f(0.99) = 1.0677 \end{array} \right.
spline{f(0.596)=0.6285f(0.99)=1.0677
题目(2)
Work2.m
x = [1, 2, 3 ,4 ,5,6,7 ];
y = [0.368,0.135,0.050,0.018,0.007,0.002, 0.001 ];
xh = [1.8, 6.15];
lagrange(x, y, xh)
结果截图:
所以可得:文章来源:https://www.toymoban.com/news/detail-727230.html
l a g r a n g e { f ( 1.8 ) = 0.1648 f ( 6.15 ) = 0.0013 {\bf{lagrange}}\left\{ \begin{array}{l} f(1.8) = 0.1648\\ f(6.15) = 0.0013 \end{array} \right. lagrange{f(1.8)=0.1648f(6.15)=0.0013文章来源地址https://www.toymoban.com/news/detail-727230.html
到了这里,关于基于Matlab的插值问题(Lagrange插值法、三次插值多项式)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!