1. Toy模板网首页
  2. > Toy博客

Hermite矩阵的酉对角化

8月前 作者：River Chandler 分类：Toy博客 阅读(25) 违法举报

这篇具有很好参考价值的文章主要介绍了Hermite矩阵的酉对角化。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

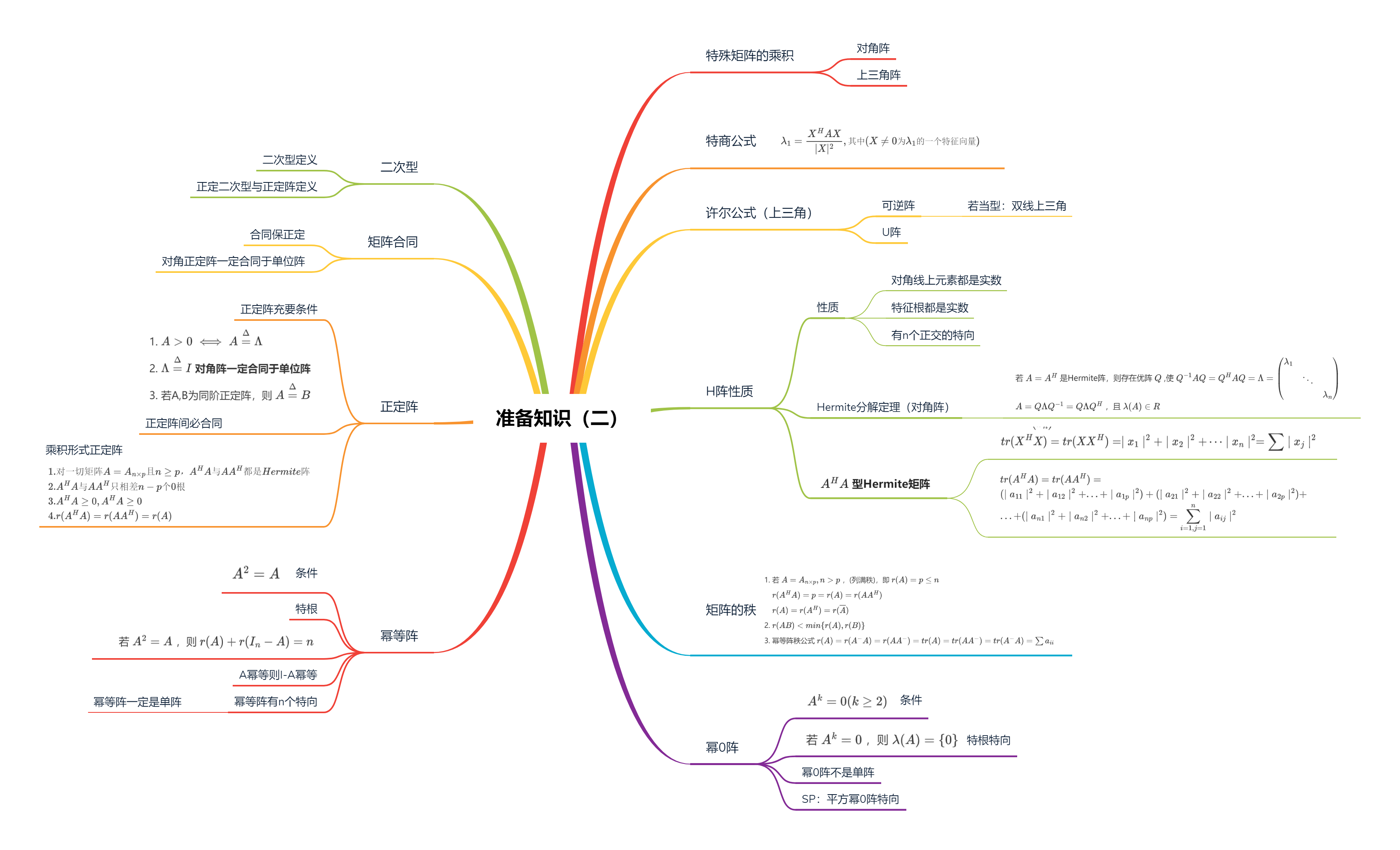
回顾有关定义

  • Hermite矩阵：一个矩阵将被称作Hermite矩阵，如果他的共轭转置等于他本身

  • 对角化：对于矩阵M(n,n)若存在一个可逆矩阵A，使得A^(-1)MA为对角矩阵，则上一操作被称为矩阵的对角化

  • 方阵可被对角化的条件：这个(n,n)矩阵存在n个线性不相关的特征向量

  • 酉矩阵：一个矩阵将被称作酉矩阵如果其中列向量的模都为1且相互正交。实数域上的酉矩阵被称作正交矩阵

  • 相似对角化

对于矩阵A，存在可逆矩阵P 使得Hermite矩阵的酉对角化,# 矩阵分析,# 量子力学,矩阵,线性代数,Powered by 金山文档

  • 酉相似对角化：

对于矩阵A，存在正交矩阵Q 使得Hermite矩阵的酉对角化,# 矩阵分析,# 量子力学,矩阵,线性代数,Powered by 金山文档

实对称矩阵的对角化

  • 求特征值

  • 求特征向量

  • 将同一个特征值所对应的不同特征向量正交化（施密特正交化）

  • 将正交特征向量规范化

施密特(schmidt)正交化

  1. 选取一个线性无关的向量组：Hermite矩阵的酉对角化,# 矩阵分析,# 量子力学,矩阵,线性代数,Powered by 金山文档

  1. Hermite矩阵的酉对角化,# 矩阵分析,# 量子力学,矩阵,线性代数,Powered by 金山文档

  1. 对于每一个向量，将其单位化

量子力学基本定义

  1. Hermite矩阵的酉对角化,# 矩阵分析,# 量子力学,矩阵,线性代数,Powered by 金山文档

  1. Hermite矩阵的酉对角化,# 矩阵分析,# 量子力学,矩阵,线性代数,Powered by 金山文档

  1. 几率密度Hermite矩阵的酉对角化,# 矩阵分析,# 量子力学,矩阵,线性代数,Powered by 金山文档

  1. Hermite矩阵的酉对角化,# 矩阵分析,# 量子力学,矩阵,线性代数,Powered by 金山文档

  1. Hermite矩阵的酉对角化,# 矩阵分析,# 量子力学,矩阵,线性代数,Powered by 金山文档

  1. Hermite矩阵的酉对角化,# 矩阵分析,# 量子力学,矩阵,线性代数,Powered by 金山文档

量子力学名词解释

  • Hermitian operator

  • 厄米算符是一种等于自己的厄米共轭的算符.量子力学中表示力学量的算符都是厄米算符

  • Uncertainty principle

  • 设两厄米算符的对易关系为:Hermite矩阵的酉对角化,# 矩阵分析,# 量子力学,矩阵,线性代数,Powered by 金山文档

  • 不确定关系:Hermite矩阵的酉对角化,# 矩阵分析,# 量子力学,矩阵,线性代数,Powered by 金山文档

  • Parity

  • 将一个函数的所有坐标宗量改变符号的运算称为空间反演,若算符Hermite矩阵的酉对角化,# 矩阵分析,# 量子力学,矩阵,线性代数,Powered by 金山文档表示该运算Hermite矩阵的酉对角化,# 矩阵分析,# 量子力学,矩阵,线性代数,Powered by 金山文档,其本征值为\pm 1 属于本征值1的\psi_1具有偶宇称 属于本征值-1的\psi_2具有奇宇称

  • 表象

  • 态和力学量的具体表示方式

  • 幺正矩阵

  • 矩阵的厄米共轭矩阵等于逆矩阵

  • ⺓正变换联系不同的表象，表象之间的⺓正变换不改变算符的本征值，也不改变矩阵的迹，矩阵⽅程式经⺓正变换保持不变

  • 微扰理论

  • 从简单问题的精确解出发来求复杂问题的近似解

  • 好量⼦数

  • 测量值的⼏率分布不随时间变化，守恒量的量⼦数称为好量⼦数

  • 全同性原理

  • 在全同粒⼦组成的体系中，两个全同的粒⼦相互代换不会引起物理状态的改变，即不引起任何可观测到的物理效应。

  • 交换简并

Hermite 算符

  • 实验上可观测的物理量的算符

  • 现选取一个力学量完全集Hermite矩阵的酉对角化,# 矩阵分析,# 量子力学,矩阵,线性代数,Powered by 金山文档,其Hermite算符记为Hermite矩阵的酉对角化,# 矩阵分析,# 量子力学,矩阵,线性代数,Powered by 金山文档

  • 任意态矢可以表示成Hermite矩阵的酉对角化,# 矩阵分析,# 量子力学,矩阵,线性代数,Powered by 金山文档

  • 由各Hermite矩阵的酉对角化,# 矩阵分析,# 量子力学,矩阵,线性代数,Powered by 金山文档组成的列矢量就是Hermite矩阵的酉对角化,# 矩阵分析,# 量子力学,矩阵,线性代数,Powered by 金山文档在表象中的波函数

  • 任何力学量算符Hermite矩阵的酉对角化,# 矩阵分析,# 量子力学,矩阵,线性代数,Powered by 金山文档在表象中的矩阵表示记为Hermite矩阵的酉对角化,# 矩阵分析,# 量子力学,矩阵,线性代数,Powered by 金山文档,其矩阵元Hermite矩阵的酉对角化,# 矩阵分析,# 量子力学,矩阵,线性代数,Powered by 金山文档

算符的运算规则

  • 线性算符

  • 单位算符

  • 算符相等

  • 算符和

  • 交换律

  • 结合律

  • 算符积

  • 算符积不满足交换律

  • 对易子Hermite矩阵的酉对角化,# 矩阵分析,# 量子力学,矩阵,线性代数,Powered by 金山文档

  • 对易恒等式

  • Hermite矩阵的酉对角化,# 矩阵分析,# 量子力学,矩阵,线性代数,Powered by 金山文档

  • 转置算符

  • Hermite矩阵的酉对角化,# 矩阵分析,# 量子力学,矩阵,线性代数,Powered by 金山文档

  • Hermite矩阵的酉对角化,# 矩阵分析,# 量子力学,矩阵,线性代数,Powered by 金山文档

表象理论

  • 微观粒子体系的状态(量子态)和力学量的具体表示形式称为表象

参考文献

米斌周 杨文光 Hermite 矩阵酉相似对角化的物理意义 华北科技学院学报 2011 年 10 月文章来源地址https://www.toymoban.com/news/detail-727307.html

到了这里，关于Hermite矩阵的酉对角化的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处： 如若内容造成侵权/违法违规/事实不符，请点击违法举报进行投诉反馈，一经查实，立即删除！

分享到：
领支付宝红包 赞助服务器费用

相关文章

  • 量子力学的实验验证：双缝实验和贝尔不等式

    量子力学的实验验证：双缝实验和贝尔不等式

    亲爱的读者， 欢迎回到我们的量子力学系列文章。在前几篇文章中，我们介绍了量子力学的起源、基本概念，以及叠加态、超级定位和量子纠缠等奇特现象。今天，我们将深入探讨量子力学的实验验证，重点介绍双缝实验和贝尔不等式实验。 双缝实验是量子力学中最具代表

    2024年02月15日
    浏览(30)

  • 我借助 AI 神器，快速学习《阿里的 Java 开发手册》，比量子力学还夸张

    我平时经常要看 PDF，但是我看书贼慢，一个 PDF 差不多几十上百页，看一遍要花挺长时间。 我记性还不好，看完之后，过些日子就记不清 PDF 是讲什么的了。为了找到 PDF 里的某些信息，又得再花时间。 不过，现在这些问题都不是问题了。 因为我最近发现了一个神器，1 分钟

    2024年02月08日
    浏览(28)
  • [小尘送书-第二期]《从零开始读懂量子力学》由浅入深，解释科学原理；从手机到超导，量子无处不在；从微观到宏观，遐想人生的意义！

    [小尘送书-第二期]《从零开始读懂量子力学》由浅入深，解释科学原理；从手机到超导，量子无处不在；从微观到宏观，遐想人生的意义！

    大家好，我是小尘，欢迎关注，一起交流学习！欢迎大家在CSDN后台私信我！一起讨论学习，讨论如何找到满意的工作！ 从微小的原子到浩瀚的宇宙，从每一滴水到闪亮的钻石，从划破夜空的激光到你身边的手机……所有事物的背后都有量子力学在主宰！你看过世界级畅销书

    2024年02月15日
    浏览(36)
  • 【矩阵分析】线性空间、λ矩阵、内积空间、Hermite矩阵、矩阵分解、矩阵范数、矩阵函数

    【矩阵分析】线性空间、λ矩阵、内积空间、Hermite矩阵、矩阵分解、矩阵范数、矩阵函数

    单纯矩阵 ：A可对角化⇔①A可对角化；⇔②n个线性无关的特征向量； ⇔③每个特征值的几何重复度等于代数重复度；⇔④特征值λi对应的pi = n - rank(λiE - A)。 等价矩阵 ：A(λ)等价于B(λ)⇔① 任意k阶行列式因子相同Dk(λ)；⇔②有相同的不变因子dk(λ)；⇔③相同的初等因子，且

    2024年01月22日
    浏览(51)

  • 矩阵理论| 特殊矩阵：Hermite矩阵/共轭对称矩阵

    Hermite矩阵是复数域上的“对称矩阵” Hermite矩阵性质 其性质 与实对称矩阵基本一致 ： 实数特征值； 有一套正交的特征向量（各个特征子空间正交+代数重数=几何重数） 此外，Hermite矩阵也是复正定矩阵的前提（就如实数域中对称矩阵是正定矩阵的前提）： A boldsymbol{A} A 为

    2024年02月06日
    浏览(35)

  • 3.Hermite矩阵

    将线性代数中的实矩阵扩展为复矩阵 【定义】A H 矩阵 对复矩阵 A A A A = [ a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋮ ⋮ ⋮ a n 1 a n 2 ⋯ a n n ] A= begin{bmatrix} a_{11} a_{12} cdots a_{1n} \\\\ a_{21} a_{22} cdots a_{2n} \\\\ vdots vdots vdots \\\\ a_{n1} a_{n2} cdots a_{nn} \\\\ end{bmatrix} A = ​ a 11 ​ a 21 ​ ⋮ a n 1 ​

    2024年01月15日
    浏览(25)
  • 【矩阵论】1. 准备知识——复数域上矩阵,Hermite变换

    【矩阵论】1. 准备知识——复数域上矩阵,Hermite变换

    矩阵论的所有文章，主要内容参考北航赵迪老师的课件 [注]由于矩阵论对计算机比较重要，所以选修了这门课，但不是专业搞数学的，所以存在很多口语化描述，而且对很多东西理解不是很正确与透彻，欢迎大家指正。我可能间歇性忙，但有空一定会回复修改的。 矩阵论 1

    2024年01月16日
    浏览(27)

  • 高等数学：矩阵的酉不变范数，樊畿控制定理，次可乘性质，p次对称度规函数

    设 ∥ ⋅ ∥ : C m × n → R + lVertcdotrVert : mathbb{C}^{mtimes n} to mathbb{R}_+ ∥ ⋅ ∥ : C m × n → R + ​ 是范数，且 ∥ ★ ∥ = ∥ U ∗ ★ V ∥ lVert bigstar rVert = lVert U^{*} bigstar V rVert ∥ ★ ∥ = ∥ U ∗ ★ V ∥ 对所有酉矩阵 U , V U,V U , V 成立（此时称 ∥ ⋅ ∥ lVertcdotrVert ∥ ⋅

    2024年02月11日
    浏览(27)
  • 【矩阵论】1.准备知识——Hermite阵，二次型，矩阵合同，正定阵，幂0阵，幂等阵，矩阵的秩

    【矩阵论】1.准备知识——Hermite阵，二次型，矩阵合同，正定阵，幂0阵，幂等阵，矩阵的秩

    矩阵论的所有文章，主要内容参考北航赵迪老师的课件 [注]由于矩阵论对计算机比较重要，所以选修了这门课，但不是专业搞数学的，所以存在很多口语化描述，而且对很多东西理解不是很正确与透彻，欢迎大家指正。我可能间歇性忙，但有空一定会回复修改的。 矩阵论 1

    2024年02月03日
    浏览(89)

  • Python生成对角矩阵和对角块矩阵

    scipy中的函数 在 scipy.linalg 中，通过 tri(N, M=None, k=0, dtype=None) 可生成 N × M Ntimes M N × M 对角矩阵，若 M=None ，则 M M M 默认为 N N N 。 k 表示矩阵中用1填充的次对角线个数。 在 numpy 中也提供了多种对角矩阵生成函数，包括 diag , diagflat , tri , tril , triu 等， numpy.diagflat diagflat 用于

    2024年02月01日
    浏览(36)

觉得文章有用就打赏一下文章作者

支付宝扫一扫打赏

博客赞助

微信扫一扫打赏

请作者喝杯咖啡吧~博客赞助

支付宝扫一扫领取红包，优惠每天领

二维码1

领取红包

二维码2

领红包