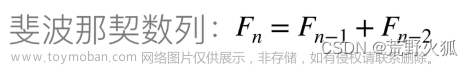数据结构和算法笔记1：滑动窗口-Toy模板网

这篇具有很好参考价值的文章主要介绍了数据结构和算法笔记1：滑动窗口。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

1. 算法原理

在一些数组或者字符串我们需要遍历子序列，可能要用到两个指针（我们称为起始指针和终止指
针）进行双层遍历，内层终止指针满足条件时跳出内层循环，然后起始指针前进，回溯终止指针到起始指针，以此继续进行遍历，然而这样效率比较低，我们可能进行了很多不必要的比较。有没有可能只进行一次遍历呢？滑动窗口提供了一个很好的思路。

在滑动窗口算法中我们要解决以下问题：

窗口内是什么？

窗口就是满足条件的子序列。

如何移动窗口的起始位置？

当前窗口的值满足条件了，窗口的起始指针就要向前移动了（也就是该缩小窗口）。

如何移动窗口的结束位置？

窗口的结束位置就是遍历数组的终止指针，也就是一次遍历（for循环）的索引。把整个数组遍历完，终止指针到了最后一个索引，移动窗口就结束了。

代码模板：

int i = 0, j = 0;//i是终止指针，j是起始指针
for (; i < s..size(); i++)//s是序列，i是一遍遍历的终止指针
{
	//对s[i]的操作
  
  // 窗口满足条件就更新数据，起始指针要移动
  while(窗口满足条件){
  	//记录或更新数据
  	...
  	
  	//起始指针移动一位
  	j++;

	//记录或更新数据
  	...
  }
  //返回结果

2. 典型习题

牛客网-牛牛的数组匹配

数据结构和算法笔记1：滑动窗口,算法和数据结构,算法,数据结构,滑动窗口

#include <iostream>
#include <cmath>
using namespace std;

int main() {
    int n, m;
    cin >> n >> m;
    int a[n], b[m];
    int sum_a = 0; 
    int sum_b = 0;
    for (int i = 0; i < n; ++i)
    {
        cin >> a[i];
        sum_a += a[i];
    }
    for (int i = 0; i < m; ++i)
    {
        cin >> b[i];
    }
    int j = 0;
    int left = 0, right = 0;
    int res = abs(b[0] - sum_a);//初始化b子序列和sum_b和sum_a的差
    for (int i = 0; i < m; i++)
    {
        sum_b += b[i];

        while (sum_b >= sum_a)//找到sum_b中超过sum_a的分界线，sum_b-b[i]<sum_a，sum_b>=sum_a
        {
            
            if (sum_b - b[i] > 0) //sum_b由两个及以上的数相加而成（sum_b >= sum_a）
            {
                if (abs(sum_b - b[i] - sum_a) < abs(sum_b - sum_a))//sum_b-b[i]比sum_b更接近sum_a
                {
                    if (abs(sum_b - b[i] - sum_a) < res)//找到更接近sum_a的和：sum_b - b[i]，更新起始指针和终止指针
                    {
                        right = i - 1;
                        left = j;
                        res = abs(sum_b - b[i] - sum_a);
                    }
                    sum_b -= b[j++];
                }
                else if (abs(sum_b - b[i] - sum_a) > abs(sum_b - sum_a))//sum_b比sum_b-b[i]更接近sum_a
                {
                    if (abs(sum_b - sum_a) < res)//找到更接近sum_a的和：sum_b，更新起始指针和终止指针
                    {
                        right = i;
                        left = j;
                        res = abs(sum_b - sum_a);
                    }
                    sum_b -= b[j++];
                }
            }
            else //sum_b由一个数相加而成（sum_b >= sum_a）
            {
                right = i;
                left = j;
                res = abs(sum_b - sum_a);
                sum_b -= b[j++];
            }
        }
        if ((i == m - 1) && (j == 0))//排除b数组所有数之和都小于a数组之和情况
        {
        	right = i;
            left = j;
        }     
    }
    
    for (int i = left; i <= right; i++)
        cout << b[i] << " ";
}

209.长度最小的子数组

数据结构和算法笔记1：滑动窗口,算法和数据结构,算法,数据结构,滑动窗口

class Solution {
public:
    int minSubArrayLen(int target, vector<int>& nums) {
    
        int i = 0;
        int j;//j一定在i的前面
        int sum = 0;
        int res = INT32_MAX;
        for (j = 0; j < nums.size(); j++)
        {
            sum = sum + nums[j];
            while (sum >= target)
            {
                if (res > (j - i + 1))
                {
                    res = (j - i + 1);
                }
                sum = sum - nums[i];
                ++i;
            }
        }
        if (res == INT32_MAX)
            return 0;
        return res;
    }
};

904.水果成篮

数据结构和算法笔记1：滑动窗口,算法和数据结构,算法,数据结构,滑动窗口

class Solution {
public:
    int totalFruit(vector<int>& fruits) {
        int len = fruits.size();
        vector<int> basket(len + 5, 0);
        int total = 0;

        int maxSum = 0;
        
        for (int i = 0, j = 0; i < len; ++i)
        {
            basket[fruits[i]]++;
            if (basket[fruits[i]] == 1)
            {
                total++;
            }
            while (total > 2)
            {
                basket[fruits[j]]--;
                if (basket[fruits[j]] == 0)
                    total--;
                j++;
            }
            maxSum = max(maxSum, i - j + 1);
        }
        return maxSum;


    }
};

76.最小覆盖子串

数据结构和算法笔记1：滑动窗口,算法和数据结构,算法,数据结构,滑动窗口文章来源地址https://www.toymoban.com/news/detail-727920.html

class Solution {
public:
    string minWindow(string s, string t) {
        unordered_map<char, int> tMp;
        for (int i = 0; i < t.size(); ++i)
            tMp[t[i]]++;
        int len = s.size();
        int minStrSize = INT_MAX;
        int ans_left = 0; // 保存最小窗口的左边界
        int ans_right = -1; // 保存最小窗口的右边界
        string res;
        for (int i = 0, j = 0; i < s.size(); ++i)
        {
            if (tMp.find(s[i]) != tMp.end())
            {
                tMp[s[i]]--;
                
            }
            while (match(tMp))
            {
                if (i - j + 1 < minStrSize)
                {
                    ans_left = j;
                    ans_right = i;
                    minStrSize = i - j + 1;
                    
                }
                if (tMp.find(s[j]) != tMp.end())
                {
                    tMp[s[j]]++;
                }
                ++j;
            } 
        }
        return s.substr(ans_left, ans_right - ans_left + 1);
    }
    bool match(unordered_map<char, int>& map)
    {
        for (auto &p: map)
        {
            if (p.second > 0)
                return false;
        }
        return true;
    }
};