ORB-SLAM之SVD奇异值分解——理论 (一）

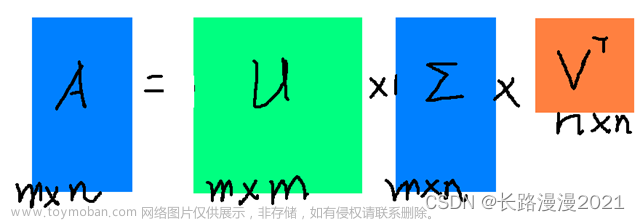
在学习《视觉SLAM十四讲》过程中常遇到SVD奇异值分解，经过一段时间的学习，在此进行记录整理, 本篇主要整理SVD的数学理论基础， 下一篇 进行整理 SVD 实际应用 。

一、线性代数的方阵分解

给定一大小为 $m\times m$ 的矩阵$A$(方阵)，其对角化分解可以写成 $A=U\Lambda U^{-1}$

其中，$U$的每一列都是特征向量，$\Lambda$对角线上的元素是从大到小排列的特征值，若将$U$记作$U=(u_1,u_2,...,u_m)$，则

A U = A ( u ⃗ 1 , u ⃗ 2 , . . . , u ⃗ m ) = ( λ 1 u ⃗ 1 , λ 2 u ⃗ 2 , . . . , λ m u ⃗ m ) = ( u ⃗ 1 , u ⃗ 2 , . . . , u ⃗ m ) [ λ 1 ⋯ 0 ⋮ ⋱ ⋮ 0 ⋯ λ m ] AU=A(\vec{u}_1,\vec{u}_2,...,\vec{u}_m)=(\lambda_1 \vec{u}_1,\lambda_2 \vec{u}_2,...,\lambda_m \vec{u}_m)=(\vec{u}_1,\vec{u}_2,...,\vec{u}_m)\left[ \begin{array}{ccc} \lambda_1 & \cdots & 0 \\ \vdots & \ddots & \vdots \\ 0 & \cdots & \lambda_m \\ \end{array} \right] AU=A(u 1​,u 2​,...,u m​)=(λ1​u 1​,λ2​u 2​,...,λm​u m​)=(u 1​,u 2​,...,u m​) ​λ1​⋮0​⋯⋱⋯​0⋮λm​​ ​

$$\Rightarrow AU=U\Lambda \Rightarrow A=U\Lambda U^{-1}$$

尤其，当矩阵$A$是一个对称矩阵时，则存在一个对称对角化分解，即 $A=Q\Lambda Q^T$

其中，$Q$的每一列都是相互正交的特征向量，且是单位向量，$\Lambda$对角线上的元素是从大到小排列的特征值。

将矩阵$Q$记作 $Q=\left(q_1,q_2,...,q_m\right)$，则矩阵$A$ 可写成如下形式：

$$A={\lambda }_1{q}_1{q}_1^T+{\lambda }_2{q}_2{q}_2^T+...+{\lambda }_m{q}_m{q}_m^T$$

 
如，给定一大小为$2\times 2$的矩阵$A=\left[\begin{array}{cc}2& 1\\ 1& 2\end{array}\right]$
根据 ∣ λ I − A ∣ = ∣ λ − 2 − 1 − 1 λ − 2 ∣ = 0 \left|\lambda I-A\right|=\left| \begin{array}{cc} \lambda-2 & -1 \\ -1 & \lambda-2 \\ \end{array} \right|=0 ∣λI−A∣= ​λ−2−1​−1λ−2​ ​=0

求得特征值为 ${\lambda }_1=3，{\lambda }_2=1$，相应地，$$q_1={\left(\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2}\right)}^T，q_2={\left(-\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2}\right)}^T$$

则 $$A={\lambda }_1{q}_1{q}_1^T+{\lambda }_2{q}_2{q}_2^T=\left[\begin{array}{cc}2& 1\\ 1& 2\end{array}\right]$$
这样，我们就得到了矩阵A的对称对角化分解。

二、奇异值分解定义

对于对称方阵而言，能够进行对称对角化分解，试想：对称对角化分解与奇异值分解有什么本质关系呢？
当给定一个大小为 $m\times n$ 的矩阵$A$，虽然矩阵$A$不一定是方阵，但大小为 $m\times m$的$A{A}^T$ 和 $n\times n$的$A^{T}A$ 却是对称矩阵，若$A{A}^T=P{\Lambda }_1{P}^T$，$A^{T}A=Q{\Lambda }_2{Q}^T$，则矩阵$A$的奇异值分解为
$$A=P\Sigma Q^T$$

其中，

• 矩阵$P=\left(p_1,p_2,...,p_m\right)$ 大小为$m\times m$，列向量 $p_1,p_2,...,p_m$ 是$A{A}^T$的特征向量，被称为矩阵$A$的左奇异向量(left singular vector)；
• 矩阵$Q=\left(q_1,q_2,...,q_n\right)$ 大小为$n\times n$，列向量 $q_1,q_2,...,q_n$ 是$A^{T}A$的特征向量，被称为矩阵A的右奇异向量(right singular vector)；
• 矩阵${\Lambda }_1$大小为$m\times m$，矩阵${\Lambda }_2$大小为$n\times n$，两个矩阵对角线上的非零元素相同 (即矩阵$A{A}^T$和矩阵$A^{T}A$的非零特征值相同)；
• 矩阵$\Sigma$ 大小为$m\times n$，位于对角线上的元素被称为 奇异值(singular value)。

为什么 $A{A}^T=P{\Lambda }_1{P}^T$，$A^{T}A=Q{\Lambda }_2{Q}^T$ ,矩阵$A$的奇异值分解 $A=P\Sigma Q^T$?
自己未理解透，自己反推理解如下：
 
 假设 $A=P\Sigma Q^T$，则
   $A{A}^T=P\Sigma Q^T(P\Sigma Q^T{)}^T=P\Sigma Q^T(Q{\Sigma }^T{P}^T)=P\Sigma {\Sigma }^T{P}^T=P{\Lambda }_1{P}^T$    （$Q^{T}Q=I$）
 同理，
   $A^{T}A=(P\Sigma Q^T{)}^{T}P\Sigma Q^T=(Q{\Sigma }^T{P}^T)P\Sigma Q^T=Q{\Sigma }^T\Sigma Q^T=Q{\Lambda }_2{Q}^T$    （$P^{T}P=I$）
 
这样理解不知是否正确，还望指正

接下来，我们来看看矩阵$\Sigma$与矩阵$A{A}^T$和矩阵$A^{T}A$的关系。
令常数$k$是矩阵$A$的秩，则 $k⩽min(m,n)$，当$m\ne n$时，矩阵${\Lambda }_1$和矩阵${\Lambda }_2$的大小不同，但矩阵${\Lambda }_1$和矩阵${\Lambda }_2$对角线上的非零元素却是相同的，若矩阵${\Lambda }_1$（或矩阵${\Lambda }_2$）对角线上的非零元素分别为${\lambda }_1,{\lambda }_2,...,{\lambda }_k$，其中，这些特征值也都是非负的，再令矩阵$\Sigma$对角线上的非零元素分别为${\sigma }_1,{\sigma }_2,...,{\sigma }_k$，则
$${\sigma }_1=\sqrt{{\lambda }_1},{\sigma }_2=\sqrt{{\lambda }_2},...,{\sigma }_k=\sqrt{{\lambda }_k}$$

即非零奇异值的平方对应着矩阵${\Lambda }_1$（或矩阵${\Lambda }_2$）的非零特征值，到这里，我们就不难看出奇异值分解与对称对角化分解的关系了，即我们可以由对称对角化分解得到我们想要的奇异值分解。

为便于理解，给定一大小为 $2\times 2$的矩阵$A=\left[\begin{array}{cc}4& 4\\ -3& 3\end{array}\right]$ (该矩阵是方阵但不是对称矩阵)

对$A{A}^T=\left[\begin{array}{cc}32& 0\\ 0& 18\end{array}\right]$进行对称对角化分解，
得到特征值为 ${\lambda }_1=32，{\lambda }_2=18$，相应地，特征向量为 $p_1={\left(1,0\right)}^T$，$p_2={\left(0,1\right)}^T$；
 

对$A^{T}A=\left[\begin{array}{cc}25& 7\\ 7& 25\end{array}\right]$进行对称对角化分解，得到特征值为${\lambda }_1=32$，${\lambda }_2=18$，
相应地，特征向量为$q_1={\left(\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2}\right)}^T$，$q_2={\left(-\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2}\right)}^T$。
 

取$\Sigma =\left[\begin{array}{cc}4\sqrt{2}& 0\\ 0& 3\sqrt{2}\end{array}\right]$，则矩阵A的奇异值分解为
$$A=P\Sigma Q^T=\left(p_1,p_2\right)\Sigma {\left(q_1,q_2\right)}^T=\left[\begin{array}{cc}1& 0\\ 0& 1\end{array}\right]\left[\begin{array}{cc}4\sqrt{2}& 0\\ 0& 3\sqrt{2}\end{array}\right]\left[\begin{array}{cc}\frac{\sqrt{2}}{2}& \frac{\sqrt{2}}{2}\\ -\frac{\sqrt{2}}{2}& \frac{\sqrt{2}}{2}\end{array}\right]=\left[\begin{array}{cc}4& 4\\ -3& 3\end{array}\right]$$
 

若矩阵$A$不是一方阵，如，给定一大小为 $3\times 2$的 A = [ 1 2 0 0 0 0 ] A=\left[ \begin{array}{cc} 1 & 2 \\ 0 & 0 \\ 0 & 0 \\ \end{array} \right] A= ​100​200​ ​
由 A A T = [ 5 0 0 0 0 0 0 0 0 ] AA^T=\left[ \begin{array}{ccc} 5 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ \end{array} \right] AAT= ​500​000​000​ ​得到
特征值为 ${\lambda }_1=5，{\lambda }_2={\lambda }_3=0$，特征向量为 $p_1={\left(1,0,0\right)}^T，p_2={\left(0,1,0\right)}^T，p_3={\left(0,0,1\right)}^T$
 

由$A^{T}A=\left[\begin{array}{cc}1& 2\\ 2& 4\end{array}\right]$得到
特征值为 ${\lambda }_1=5，{\lambda }_2=0$，特征向量为 $q_1={\left(\frac{\sqrt{5}}{5},\frac{2\sqrt{5}}{5}\right)}^T，q_2={\left(-\frac{2\sqrt{5}}{5},\frac{\sqrt{5}}{5}\right)}^T$
 

令 Σ = [ 5 0 0 0 0 0 ] \Sigma=\left[ \begin{array}{cc} \sqrt{5} & 0 \\ 0 & 0 \\ 0 & 0 \\ \end{array} \right] Σ= ​5 ​00​000​ ​（矩阵$\Sigma$大小为$3\times 2$）

此时，矩阵$A$的奇异值分解为
A = P Σ Q T = ( p ⃗ 1 , p ⃗ 2 ) Σ ( q ⃗ 1 , q ⃗ 2 ) T = [ 1 0 0 0 1 0 0 0 1 ] [ 5 0 0 0 0 0 ] [ 5 5 2 5 5 − 2 5 5 5 5 ] = [ 1 2 0 0 0 0 ] A=P\Sigma Q^T=\left(\vec{p}_1,\vec{p}_2\right)\Sigma \left(\vec{q}_1,\vec{q}_2\right)^T =\left[ \begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{array} \right] \left[ \begin{array}{cc} \sqrt{5} & 0 \\ 0 & 0 \\ 0 & 0 \\ \end{array} \right] \left[ \begin{array}{cc} \frac{\sqrt{5}}{5} & \frac{2\sqrt{5}}{5} \\ -\frac{2\sqrt{5}}{5} & \frac{\sqrt{5}}{5} \\ \end{array} \right] =\left[ \begin{array}{cc} 1 & 2 \\ 0 & 0 \\ 0 & 0 \\ \end{array} \right] A=PΣQT=(p ​1​,p ​2​)Σ(q ​1​,q ​2​)T= ​100​010​001​ ​ ​5 ​00​000​ ​[55 ​​−525 ​​​525 ​​55 ​​​]= ​100​200​ ​

特别的，假设给定一对称矩阵 $A=\left[\begin{array}{cc}2& 1\\ 1& 2\end{array}\right]$ (对称矩阵)，分别计算 $A{A}^T$和$A^{T}A$，会发现：

  ① $A{A}^T=A^{T}A=\left[\begin{array}{cc}2& 1\\ 1& 2\end{array}\right]\left[\begin{array}{cc}2& 1\\ 1& 2\end{array}\right]=\left[\begin{array}{cc}5& 4\\ 4& 5\end{array}\right]$

  ② 左奇异向量和右奇异向量构成的矩阵相等，即 $P=Q=\left[\begin{array}{cc}\frac{\sqrt{2}}{2}& -\frac{\sqrt{2}}{2}\\ \frac{\sqrt{2}}{2}& \frac{\sqrt{2}}{2}\end{array}\right]$

  ③ 该矩阵的奇异值分解和对称对角化分解相同，即 $A=\left[\begin{array}{cc}\frac{\sqrt{2}}{2}& -\frac{\sqrt{2}}{2}\\ \frac{\sqrt{2}}{2}& \frac{\sqrt{2}}{2}\end{array}\right]\left[\begin{array}{cc}3& 0\\ 0& 1\end{array}\right]\left[\begin{array}{cc}\frac{\sqrt{2}}{2}& \frac{\sqrt{2}}{2}\\ -\frac{\sqrt{2}}{2}& \frac{\sqrt{2}}{2}\end{array}\right]$

这是由于对于正定对称矩阵而言，奇异值分解和对称对角化分解结果相同。

三、奇异值分解低秩逼近

在对称对角化分解中，若给定一个大小为 $3\times 3$的矩阵 A = [ 30 0 0 0 20 0 0 0 1 ] A=\left[ \begin{array}{ccc} 30 & 0 & 0 \\ 0 & 20 & 0 \\ 0 & 0 & 1 \\ \end{array} \right] A= ​3000​0200​001​ ​

矩阵$A$的秩为 $rank\left(A\right)=3$，特征值为 ${\lambda }_1=30，{\lambda }_2=20，{\lambda }_3=1$，对应特征向量分别为 $q_1={\left(1,0,0\right)}^T，q_2={\left(0,1,0\right)}^T，q_3={\left(0,0,1\right)}^T$

考虑任意一向量 $v={\left(2,4,6\right)}^T=2q_1+4q_2+6q_3$，则
$$Av=A\left(2q_1+4q_2+6q_3\right)=2{\lambda }_1{q}_1+4{\lambda }_2{q}_2+6{\lambda }_3{q}_3=60q_1+80q_2+6q_3$$

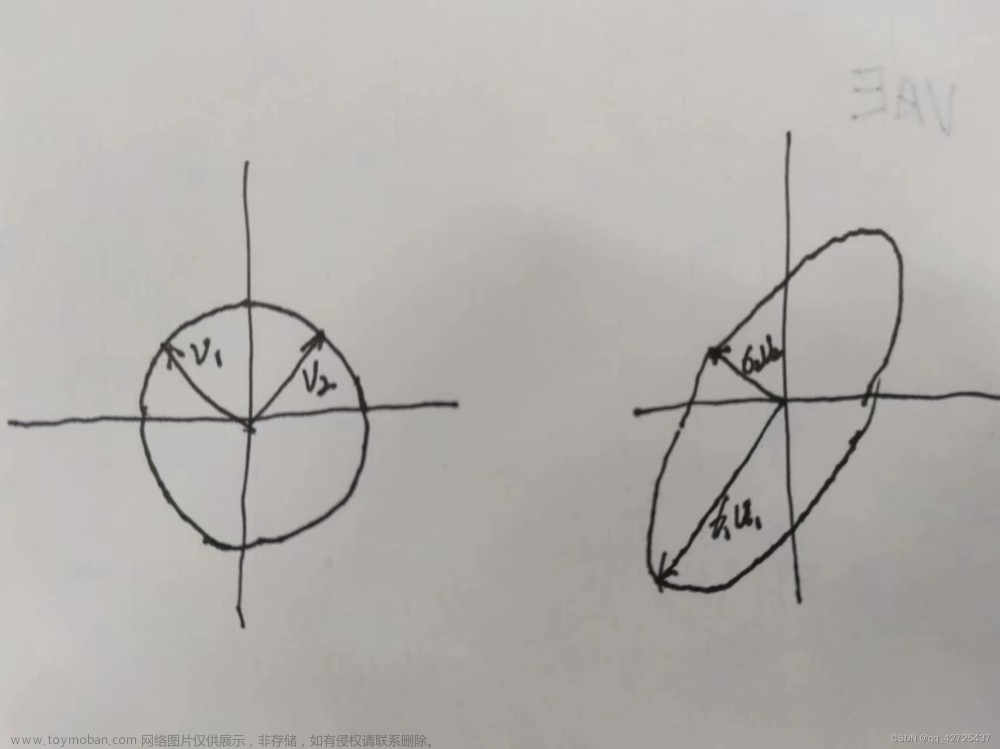
上述表明：用矩阵去乘以任意一向量的效果取决于较大的特征值及其特征向量，类似地，在奇异值分解中 较大的奇异值会决定原矩阵的“主要特征”，即 奇异值分解的低秩逼近(也称为截断奇异值分解)。
给定一个大小为 $m\times n$的矩阵$A$，由于 $A=P\Sigma Q^T$可以写成
$$A=\sum _{i=1}^k{\sigma }_i{p}_i{q}_i^T={\sigma }_1{p}_1{q}_1^T+{\sigma }_2{p}_2{q}_2^T+...+{\sigma }_k{p}_k{q}_k^T$$

其中，
向量 $p_1,p_2,...,p_k$之间相互正交，向量 $q_1,q_2,...,q_k$之间也相互正交，
由内积 $⟨{\sigma }_i{p}_i{q}_i^T,{\sigma }_j{p}_j{q}_j^T⟩=0,1\le i\le k,1\le j\le k,i\ne j$ 得到矩阵A的F-范数的平方为
$$||A|{|}_F^2=||{\sigma }_1{p}_1{q}_1^T+{\sigma }_2{p}_2{q}_2^T+...+{\sigma }_k{p}_k{q}_k^T|{|}_F^2$$$$={\sigma }_1^2||p_1{q}_1^T|{|}_F^2+{\sigma }_2^2||p_2{q}_2^T|{|}_F^2+...+{\sigma }_k^2||p_k{q}_k^T|{|}_F^2={\sigma }_1^2+{\sigma }_2^2+...+{\sigma }_k^2=\sum _{i=1}^r{\sigma }_i^2$$

可知，矩阵$A$的F-范数的平方 等于 其所有奇异值的平方和

假设 $A_1={\sigma }_1{p}_1{q}_1^T$是矩阵A的一个秩一逼近（rank one approximation），那么，它所带来的误差则是${\sigma }_2^2+{\sigma }_3^2+...+{\sigma }_k^2$（$k$是矩阵$A$的秩），如何证明$A_1={\sigma }_1{p}_1{q}_1^T$是最好的秩一逼近呢？

由于$||A-A_1|{|}_F^2=||P\Sigma Q^T-A_1|{|}_F^2=||\Sigma -P^T{A}_{1}Q|{|}_F^2$

令$P^T{A}_{1}Q=\alpha x{y}^T$，其中，$\alpha$是一个正常数，向量 $x$ 和 $y$ 分别是大小为 $m\times 1$和$n\times 1$的单位向量，则

$||\Sigma -P^T{A}_{1}Q|{|}_F^2=||\Sigma -\alpha x{y}^T|{|}_F^2=||\Sigma |{|}_F^2+{\alpha }^2-2\alpha ⟨\Sigma ,x{y}^T⟩$

单独看大小为$m\times n$的矩阵 $\Sigma$和$x{y}^T$的内积 $⟨\Sigma ,x{y}^T⟩$，会发现

$$⟨\Sigma ,x{y}^T⟩=\sum _{i=1}^k{\sigma }_i{x}_i{y}_i\le \sum _{i=1}^k{\sigma }_i\left|x_i\right|\left|y_i\right|$$ $$\le {\sigma }_1\sum _{i=1}^k\left|x_i\right|\left|y_i\right|={\sigma }_1⟨x^{\ast },y^{\ast }⟩\le {\sigma }_1||x^{\ast }||\cdot ||y^{\ast }||\le {\sigma }_1||x||\cdot ||y||={\sigma }_1$$

其中，
  ① $x_i,y_i$分别是向量$x$和$y$的第$i$个元素；
  ② 向量$x^{\ast }={\left(\left|x_1\right|,\left|x_2\right|,...,\left|x_k\right|\right)}^T$的大小为$k\times 1$，向量$y^{\ast }={\left(\left|y_1\right|,\left|y_2\right|,...,\left|y_k\right|\right)}^T$的大小也为$k\times 1$，另外，以$x^{\ast }$为例，$||x^{\ast }||=\sqrt{x_1^2+x_2^2+...+x_k^2}$是向量的模，则$||A-A_1|{|}_F^2$（残差矩阵的平方和）为

$$||\Sigma -\alpha x{y}^T|{|}_F^2\ge ||\Sigma |{|}_F^2+{\alpha }^2-2\alpha {\sigma }_1=||\Sigma |{|}_F^2+{\left(\alpha -{\sigma }_1\right)}^2-{\sigma }_1^2$$

当且仅当$\alpha ={\sigma }_1$时，$||A-A_1|{|}_F^2$取得最小值${\sigma }_2^2+{\sigma }_3^2+...+{\sigma }_k^2$，此时，矩阵$A$的秩一逼近恰好是$A_1={\sigma }_1{p}_1{q}_1^T$。

当然，可以证明$A_2={\sigma }_2{p}_2{q}_2^T$是矩阵$A-A_1$的最佳秩一逼近，
以此类推，$A_r={\sigma }_r{p}_r{q}_r^T,r<k$ 是矩阵 $A-A_1-A_2-...-A_{r-1}$的最佳秩一逼近。

由于矩阵$A_1+A_2+...+A_r$的秩为 $r$，这样，可以得到矩阵$A$的最佳秩$r$逼近（rank-r approximation），即
$$A\approx A_1+A_2+...+A_r=\sum _{i=1}^r{A}_i$$这里得到的矩阵$P_r$的大小为$m\times r$，矩阵${\Sigma }_r$的大小为$r\times r$，矩阵$Q_r$的大小为$n\times r$，矩阵A可以用$P_r{\Sigma }_r{Q}_r^T$来做近似。

用低秩逼近去近似矩阵A有什么价值呢？
给定一个很大的矩阵，大小为$m\times n$，需要存储的元素数量是$mn$个，当矩阵$A$的秩$k$远小于$m$和$n$，只需要存储 $k(m+n+1)$个元素就能得到原矩阵$A$，即$k$个奇异值、$km$个左奇异向量的元素和kn个右奇异向量的元素；若采用一个秩$r$矩阵$A_1+A_2+...+A_r$去逼近，我们则只需要存储更少的$r(m+n+1)$个元素。因此，奇异值分解是一种重要的数据压缩方法。

参考链接1
参考链接2
参考链接3
参考链接4文章来源地址https://www.toymoban.com/news/detail-728602.html

到了这里，关于ORB-SLAM之SVD奇异值分解——理论 (一）的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！