题目
509. 斐波那契数
简单
相关标签
递归 记忆化搜索 数学 动态规划
斐波那契数 (通常用 F(n) 表示)形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始,后面的每一项数字都是前面两项数字的和。也就是:
F(0) = 0,F(1) = 1 F(n) = F(n - 1) + F(n - 2),其中 n > 1
给定 n ,请计算 F(n) 。
示例 1:
输入:n = 2 输出:1 解释:F(2) = F(1) + F(0) = 1 + 0 = 1
示例 2:
输入:n = 3 输出:2 解释:F(3) = F(2) + F(1) = 1 + 1 = 2
示例 3:
输入:n = 4 输出:3 解释:F(4) = F(3) + F(2) = 2 + 1 = 3
提示:
0 <= n <= 30
思路和解题方法
在这段代码中,函数
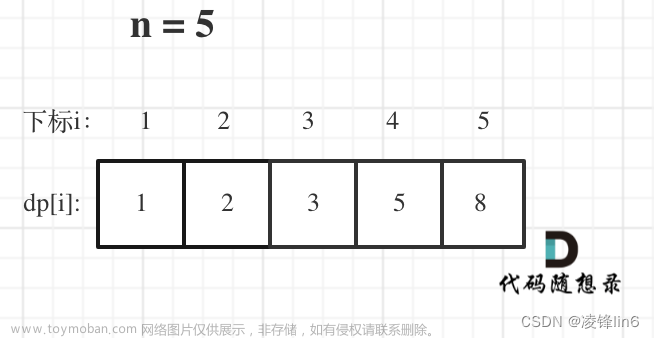
fib接受一个整数N作为参数,返回斐波那契数列中第N个数的值。如果N小于等于1,则直接返回N。if (N <= 1) return N;接下来,我们使用动态规划的思想来求解斐波那契数列。我们定义一个一维数组
dp,其中dp[i]表示斐波那契数列中第i个数的值。我们先将数组的前两个元素初始化为0和1。vector<int> dp(N + 1); dp[0] = 0; dp[1] = 1;接下来,我们使用循环遍历数组中的每个元素,计算出当前位置的值。根据斐波那契数列的定义,第i个数的值应该等于前两个数的和,即
dp[i-1] + dp[i-2]。最后,返回数组中第N个数的值。for (int i = 2; i <= N; i++) { dp[i] = dp[i - 1] + dp[i - 2]; } return dp[N];
复杂度
时间复杂度:
O(N)
时间复杂度是O(N),其中N是斐波那契数列中第N个数的值。在循环中,我们需要遍历数组中的每个元素一次,并且每次计算都需要使用前两个数的和,所以时间复杂度与N成正比。
空间复杂度
O(N)
空间复杂度也是O(N),因为我们需要使用一个数组来保存斐波那契数列中每个数的值。数组的长度为N+1,所以空间复杂度与N成正比。
c++ 代码
class Solution {
public:
int fib(int N) {
// 如果N小于等于1,则直接返回N
if (N <= 1) return N;
// 创建一个大小为N+1的数组,用于保存斐波那契数列中每个数的值
vector<int> dp(N + 1);
// 初始化数组的前两个元素为0和1
dp[0] = 0;
dp[1] = 1;
// 使用动态规划的思想计算斐波那契数列
for (int i = 2; i <= N; i++) {
// 当前位置的值等于前两个数的和
dp[i] = dp[i - 1] + dp[i - 2];
}
// 返回斐波那契数列中第N个数的值
return dp[N];
}
};
常数空间代码
只是对于dp来维护两个数
class Solution {
public:
int fib(int n) {
// 如果n小于等于1,直接返回n
if (n <= 1) return n;
// 初始化斐波那契数列的前两个数
int n1 = 0, n2 = 1;
// 用于保存当前位置的值
int ans = 0;
// 从第3个位置开始遍历到第n个位置
for (int i = 2; i <= n; i++) {
// 计算当前位置的值,即前两个数的和
ans = n1 + n2;
// 更新前两个数的值
n1 = n2;
n2 = ans;
}
// 返回斐波那契数列中第n个数的值
return ans;
}
};
附上递归解法
class Solution {
public:
int fib(int N) {
if (N < 2) return N;
return fib(N - 1) + fib(N - 2);
}
};觉得有用的话可以点点赞,支持一下。
如果愿意的话关注一下。会对你有更多的帮助。文章来源:https://www.toymoban.com/news/detail-728767.html
每天都会不定时更新哦 >人< 。文章来源地址https://www.toymoban.com/news/detail-728767.html
到了这里,关于力扣第509题 斐波那契数 新手动态规划(推荐参考) c++的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!