量化交易全流程（六）（待完善补充）

本节目录

多因子风险模型

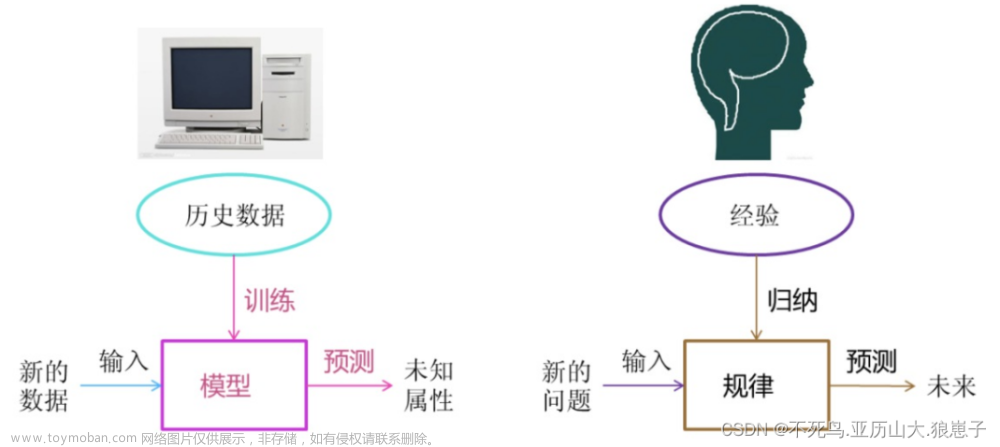
自从股票市场产生以来，大量的学者、业界人员都在研究股票的价格波动究竟是由什么决定的。一个明显的事实是，股票的价格波动一定是由多种因素决定的，比如大盘因素、市值因素和行业因素。对于大盘因素，股票的波动是会受大盘影响的。对于市值因素，不同市值的股票，波动率也会有较大的区别。对于行业因素，不同行业的股票，波动率往往也会有较大区别。
所谓多因子策略，就是要发掘诸如此类的因素（因子），确定这些因子对股价波动确实有影响，然后以一种合理的方式组合起来，形成模型，用于支持投资操作。
股价波动对应着股票的风险，所以多因子模型中的因子，往往又被称作风险因子，即这些因子共同解释了股票的风险。
本节将从最简单的风险定义开始，逐步展开介绍多因子风险模型。
风险定义
根据前面介绍的金融基本概念可知，风险可以简单定义为收益的标准差。我们可以通过计算历史收益率的标准差来获得股票的风险估计。假设一个投资组合的收益率为R，那么投资组合的风险

按照这个定义，我们可以证明，假设投资组合中有N支股票，而且这些股票是完全不相关的，每支股票本身的风险都是δ，那么投资组合的风险为：

由此可见，在投资组合中引入不相关的股票，可以降低投资组合的风险。当然实际情况中，股票不太可能完全不相关。所以我们将模型推广一下，假设所有股票的相关性都为，那么可以证明，投资组合的风险为：(证明略)

这种计算风险的方法是由马科维茨提出的。在该模型下，分散投资是可以降低风险的。然而，有些风险，无论怎么分散，都没有办法消除，因为所有股票都倾向于随着大盘的涨跌而涨跌。这种市场性的风险称为系统性风险。在马科维茨的模型中，这种系统性风险并没有体现出来。

CAPM

为了体现系统性风险，夏普等学者提出了资本资产定价模型（Capital Asset Pricing Model)，简称CAPM。CAPM体现了预期收益和市场风险之间的关系。公式如下：

其中，为资产i的系统性风险。

CAPM的核心思想是，投资者只有承担了市场风险，才能获得对应比例的超额回报。
CAPM中最核心的参数就是股票的Beta系数。Beta系数衡量了某种证券或者投资组合对于整体市场波动性的敏感程度。直观地理解就是，假设某支股票的Beta系数是1，那么市场上涨10%，股票也会对应上涨10%。如果Beta系数是2，那么市场上涨10%，股票将会对应上涨20%，如果市场下跌10%，股票也会对应下跌20%。
计算Beta系数也是CAPM中最重要的一环。一种简单的方式是选取一段历史样本，使用公式进行计算。同时，也要注意到，Beta系数不一定是稳定的，而且不同的历史样本，算出来的 Beta 系数肯定是不一样的。所以如何更准确地估计Beta系数，并不是一个简单的问题。CAPM提供了一个新的视角来看待投资组合的风险。然而，CAPM离真实市场还是有较大的距离的。后来，美国学者斯蒂芬·罗斯（Stephen A. Ross）给出了一个以无套利定价为基础的多因素资产定价模型，也称套利定价理论（Arbitrage Pricing Theory）模型。

APT

1970年，投资界发现有类似特征的股票倾向于有类似的收益率表现（比如相同行业的、市值大小相近的，等等）。基于此发现，斯蒂芬·罗斯提出了套利定价理论（Arbitrage Pricing Theory)，简称APT。

APT的核心思想是，证券或者投资组合的预期收益率与一组未知的系统性因素相关，同时也满足一价定律，即风险—收益性质相同的资产，价格也必须相同。否则会出现套利行为。模型推导出的资产收益率取决于一系列影响资产收益的因素，而不完全依赖于市场资产的组合，而套利活动则保证了市场均衡的实现。
实际上，CAPM是APT 模型的一种特殊形式。如果假设只有市场收益率这一个因子会影响证券的收益率，那么APT模型实际上就是CAPM。所以APT模型可以算是CAPM的一种推广，将单一的市场因子推广到多种因子。APT 模型的计算公式具体如下：

为风险因子，因子载荷，敏感度，资产本身风险。

APT 的因子模型更符合人对证券投资的直觉，所以更贴合于市场。不过，虽然APT 模型提出了一个很好的框架，但该理论并没有告诉我们，因子是什么，如何计算一只股票对因子的风险头寸，所以APT还需要进行进一步的完善和研究，才能真正用于实际投资。
对于这个问题，BARRA公司进行了大量的研究，并提出了BARRA多因子模型(Multi-factor Model)。

MFM

多因子模型（Multi-Factor Model,MFM）是建立在这样的概念基础之上的，即一只股票的收益可以由一系列公共因子加上一个股票自身特殊的因子来解释。通俗地说，类似的股票应该有类似的收益率。所谓的"类似"，主要是通过股票的各个特征来表现的，包括股票价量数据、财务报表中的基本面数据等。

MFM可用于识别股票之间共同的因子，并且计算股票收益率对于这些因子的敏感度。最终的风险模型将所有股票的收益率表达为因子收益和特殊收益的加权之和。当我们得到模型之后，任何的因子变化都将能够很快反应在模型之中。

多因子模型的优势

使用多因子模型有很多种优势，具体如下。
□可以减小问题规模。假设有3000只股票，如果使用收益率来计算协方差，那么我们将会有3000x(3000-1)/2= 4 498 500个协方差。但是如果我们将股票表示为20个因子，那么我们更多地就只需要研究这20个因子之间的关系。问题的规模就小得多了。
□多因子模型对风险进行了比较全面的分解和分析。其在进行风险暴露分析的时候比诸如CAPM的模型能分析得更为全面。
□在选择因子的时候，由于引入了经济逻辑，所以多因子模型的分析不会局限于纯历史数据的挖掘。

建立多因子模型的一般流程

风险因子的种类
建立多因子模型，第一步就是要选择合适的因子。一般来说，因子可以分成三大类：反映外部影响的因子、代表资产特点的截面比较因子、纯内部因子或者统计因子。

反映外部影响的因子

很明显，外部经济力量与股票市场间应该存在明确的联系。相关的因子便试图抓住这种联系。这些因子包括但不限于通货膨胀系数、石油价格变动、汇率变化、工业生产量变化等。这些因子通常又被称为宏观因子。宏观因子有时非常有效，但其也有如下三方面的缺陷。
第一个缺陷是，必须通过回归分析或者类似的方法来估计资产收益对这些因素的反应系数。如果我们需要估计3000只股票，那么每个月都需要进行3000次时间序列回归。这将会产生估计误差。
第二个缺陷是，我们的估计通常是建立在对历史数据的估计基础之上的，比如说5年。这些估计虽然可能能够比较精确地描述历史情形，但未必能够精确描述当前或者未来的情况。也就是说，这些反应系数是不稳定的。
第三个缺陷是，一些宏观经济数据的质量较差，收集过程可能会存在错误和延迟。而且有的数据可能因为频率较低而没有太大的使用价值。

资产截面因子

资产截面因子用于比较股票自身的特征，与宏观经济无关。截面因子通常也可以分为两类：基本面特征和市场特征。基本面特征包括诸如派息比例、每股收益、股票市值等。市场特征则包括过去一段时期的收益率、波动率、成交量、换手率等。

统计因子

统计因子是一类因子，这些因子有可能与股票收益率相关，虽然其中并不存在明显的金融经济学逻辑，但是从统计上可以得到很好的解释效果。

一般来说，我们要回避统计因子，因为统计估计往往会得出一些虚假相关性，而且统计因子往往还非常难以解释。一般来说，我们需要挑选具有经济意义，可解释，而且具有统计意义的因子。典型的因子包含两类：行业因子和风险因子。行业因子用于衡量不同行业股票的不同行为，风险因子用于衡量其他的非行业尺度上不同股票的不同行为。

行业因子

股票所属行业是一项非常重要的特征。不过有的公司涉及多种行业，所以对股票进行行业分类需要一个标准。A 股票的行业的分类标准有很多种，比如申万行业分类、证监会行业分类等。
其中，申万行业在业内使用得较多。股票分类又分为一级行业分类、二级行业分类等。所谓一级行业分类就是比较粗的分类，二级行业分类相当于一级行业分类的子分类。

二级行业分类众多，这里就不列举了。
在进行回归分析的时候，行业的头寸一般设为0或1的哑变量，主要目的是检测因子的表现是否有明显的行业倾向。

风险因子分类

行业并不是产生股票风险的唯一来源，风险因子也是一大类的风险来源。一般来说，风险因子可以分为如下几个大类。
□波动率（volatility)：根据波动率的不同来区分股票。波动率的概念在前面的章节中曾提到过，是股份一项十分重要的特征。

□动量（momentum)：根据股票当前的绩效来进行区分。学术中曾有实证研究，动量效应确实是存在的，即处于涨势的股票总是会倾向于上涨得更多，处于跌势中的股票也倾向于跌得更多。
口规模（size)：股票的规模一般会使用市值来表示。著名的Fama-French三因子模型中就有市值的因子。
□流动性（liquidity)：流动性也是股票一项非常重要的指标，一般使用股票的交易量来表示。
□成长性（growth)：根据过去的和预期的收益成长性来进行区分。
□价值（value)：根据股票的一些基本面数据来区分股票。比如股息、现金流、账面价值等。
□财务杠杆（financial leverage)：根据净资产负债率和利率风险来进行区分。

每一个大类通常都会包含几个特定的度量尺度，这些特定的度量尺度称为描述符(descriptors)。例如，波动率包括近期每日收益率波动率、期权隐含的波动率、近期价格范围等。尽管同一类别中的各个描述符通常都是相关的，但是每一个描述符都描述了风险因子的某一个方面。我们也可以在某大类因子的不同描述符中分配头寸权重。

投资组合风险分析

多因子风险模型可用于分析当期投资组合风险。它既能衡量整体风险，也能利用多种途径来分散风险。风险的分散可以鉴别出资产组合中重要的风险来源。
风险分析对于消极管理和积极管理都很重要。消极管理通常可以理解为指数基金，指数基金一般与一个特定的基准组合相匹配。然而，即使有了基准组合，管理者的投资也不一定包括基准组合中的所有股票。比如，对于一个包含几百上千只股票的基准组合，管理者不太可能持有所有的股票。当前的投资组合的风险分析就可以告诉消极管理者其投资组合相对于基准组合的风险水平。这就是跟踪误差。这是投资组合与基准组合之间收益差异的波动率来源，消极的管理者的目标是最小化跟踪误差。
当然，更多的投资者所关注的可能是积极型管理。积极型管理者的目标不是尽可能地接近基准组合，而是要尽可能地超越基准组合。同样的，风险分析对于积极型管理关注积极型策略也十分重要。积极型管理者只承担他们获得超额收益所面临的风险。
通过恰当地分解当前投资组合的风险，积极型管理者可以更好地理解他们投资组合的们为什么以及如何才能改变它。资产配置。风险分析不仅可以告诉积极型管理者他们的积极型风险是什么，还可以告诉他们为什么以及如何才能改变它。

基准组合

在实际情况中，积极型资产管理者通常被要求其管理的基金绩效要高于基准组合。所谓基准组合，在实际中，其实并不是真正的"市场组合"。比如沪深300或者上证指数，并不是真正的"整体市场"的表现，毕竟A股有3000只股票，而这些指数只是包括了其中一部分的股票。另外，当我们在投资债券或者商品期货的时候，沪深300明显也不是一个合适的基准组合。所以在实际中，我们很少真正地去对"整体市场"进行比较和分析，取而代之的是人为选择出来的"基准组合"。
那么之前提到的β值，就不再是相对于整体市场的，而是相对于基准组合的了。

因子选择和测试

备选因子有两个来源。一个来源是市场信息，比如成交量、价格等，这种信息每天都有。第二个来源是公司的基本面数据，比如利润、净资产、负债等。这些信息一般会体现在季报和年报中。也有些因子是市场信息和基本面信息的组合，比如市盈率（PE)。因子的选择并不是一个简单的过程，需要进行大量严谨的量化研究。
最开始是因子的初步筛选。首先，好的因子，即使单独来看，也应该具有比较明显的意义。换句话说，好的因子应该是被广泛接受的，易于理解的资产相关的特征。其次，好的因子应该能将市场中的股票较好地进行分类，能够较明显地说明投资组合的风险特征。
选中的因子应当是基于经常发布的、准确的数据，而且应当具有预测风险的效用。当将一个因子加到模型里面的时候，对模型的预测作用应该会有所提升，否则的话就不应该加入进来。
为了能将不同的因子结合到一个模型中，我们需要对其进行归一化操作。所谓归一化，就是将不同范围的数据调整到同样的量级，这样做可便于比较。因为不同因子的数值范围差别很大，如果不进行归一化，就会极大地影响模型的有效性。归一化的公式是：

因子归一化之后，我们将资产收益和行业、因子进行回归。每次只对一个因子进行回归，这样就可以对每个因子测试其统计显著性。之后再基于计算的结果选择相应的因子纳入模型中。实际上这是一个迭代的过程，当将最显著的因子纳入模型之后，后面的因子需要接受更为严格的检验才能纳入，只有当它们能够增加模型的解释能力的时候才考虑将其纳入。

Fama-French三因子模型

Fama-French 三因子模型考虑的因子包括CAPM里的市场风险溢价因子，小市值股票回报率减去大市值股票回报因子（SMB)，以及低PE股票回报率减去高PE 股票回报率因子(HML)。由于 Eugene Fama 当时研究的对象为美国的股市，而且时代相差太过久远，因此当时有效的模型可能现在在A股中的使用已不是那么有效了，但为了遵从原本的三因子模型，我们还是尽可能原汁原味地遵照原本模型的构建方式。我们相信，数据本身在模型的学习阶段并不重要，能够掌握模型背后的思想才是更为重要的。

数据需要从锐思数据库下载存放到mysql数据库中，akshare好像还找不到因子数据，自行下载数据。从2021-01-04到2023-09-30大概60万条数据。

在A股当中还原三因子模型时，我们将资产池暂时设定为上证380相关成分股中历史数据较多的股票。其收益率我们以周收益率为准，并且假定每个因子对每只股票都是有效的，代码如下：

import numpy as np
import pandas as pd
sz380 = pd.read_excel(*'sz380.xlsx')
sh=pd.read_excel('000001sh.xlsx')[2:]
sh.columns=['date','sh_index']
sh=sh.set_index(['date'])
sh=sh.pct_change()

假定无风险年化收益率为0.02，代码如下：

sh['sh_index']=sh['sh_index']-0.02/52
sz380.rename(columns={'Unnamed:0':'date'},inplace=True)
sz380=sz380.set_index(['date'])

将整个数据集拆分为三个DataFrame，分别对应于不同的指标，也可以用Multilndex 的形式进行数据整理，代码如下：

sz380close=sz380.iloc[:,:380].iloc[2:,:]
sz380mc=sz380.iloc[:.380:760].iloc[2:,:]
sz380pe= sz380.iloc[:.760:].iloc[2:,:]
sz380mc.columns = sz380close.columns
sz380pe.columns=sz380close.columns

转化数据格式，将字符串转化为浮点数进行计算。为了准确计算，可以用Python的定点数对象进行计算，代码如下：

def to_float (df):
    for c in df.columns:
        df[c]=df[c].map(float)
to_float (sz380close)
to_float (sz380mc)
to_float (sz380pe)

我们对每只股票的数据量进行排序，选取其中一部分历史数据量较大的进行计算，可以设置为全局变量以便于调控（按照数据量排序的前两百名股票的历史数据）。由于三种数据都是行情相关的，因此对于每一只股票而言，三种数据的量都是一样的，代码如下：

top = 200
def get_data_amount_count (df,top): 
    count =[]
    for c in df.columns:
        count.append ([c,len(df[c].dropna())])
    count = sorted(count,key= lambda x:x[1],reverse=True)
    valid_ids=[]  # 获得数据量足够的股票代码
    for i in range(0,top):
        valid_ids.append (count[i][0])
    return valid_ids,count[top][1]
valid_ids,amount_of_data = get_data_amount_count (sz380close, top)

sz380close=sz380close[valid_ids].iloc[len(sz380) -amount_of_data:,:].fillna (method='ffill')
sz380return=sz380close.pct_change().dropna()
sz380mc=sz380mc[valid_ids].iloc[len(sz380)-amount_of_data:,:].fillna (method='ffill').dropna()
sz380pe=sz380pe[valid_ids].iloc[len(sz380) -amount_of_data:,:].fillna (method='ffill').dropna()

下面就来正式构建因子。我们先构建SMB 因子。SMB因子是由做多市值排名相对较小，而做空市值排名相对较大的股票获得的因子。针对数据内的每一个交易日，我们根据市值来进行选股，代码如下：

sz380mc_dict=sz380mc.to_dict (orient ='index')
factor_track=[]
for date, data in sz380mc_dict.items():
# 分别取市值排名前10％和后10%
    data=list(data.items())
    data=sorted(data,key=lambda x:x[1])
    small_cap=data[:int (0.1*len(data))]
    large_cap=data[int(0.9*len(data)):]
# 将每一个交易日的SMB因子构建出来
# 将投资轨迹建立起来
factor_track.append([date, [x[0] for x in small_cap],[x[0] for x in large_cap]])
# 再依据投资轨迹建立相应的因子收益轨迹
factor=[]
for track in factor_track:
# 做多小市值，做空大市值
# 各个组合假定为等权重
    try:
        trading_day_small_cap_return = np.mean(sz380return.loc[pd.Timestamp(track[0]),track[1]])
        trading_day_large_cap_return = np.mean (sz380return.loc[pd.Timestamp(track[0]),track[2]])
        factor.append([track[0], trading_day_small_cap_return-trading_day_large_cap_return])
    except KeyError:
        continue
smb = pd.DataFrame(factor,columns=['date','smb'])

这样我们就建立了一个因子，如法炮制，还可以建立HML因子，即做空高PE股票，做多低PE股票，代码如下：

for date, data in sz380pe_dict.items():
    # 我们分别取PE排名前10％和后10%
    data=list(data.items())
    data = sorted(data,key = lambda x:x[1])
    low_pe=data[:int(0.1*len(data))]
    high_pe=data[int(0.9*len(data)):]
    # 投资轨迹建立起来
    factor_track.append([date, [x[0] for x in low_pe],[x[0] for x in high_pe]])
# 再依据投资轨迹建立相应的因子收益轨迹
factor =[]
for track in factor_track:
    # 做多低PE，做空高PE
    # 假定各个组合为等权重
    try:
        trading_day_low_pe_return=np.mean(sz380return.loc[pd.Timestamp(track[0]),track[1]])
        trading_day_high_pe_return=np.mean(sz380return.loc[pd.Timestamp(track[0]),track[2]])
        factor.append([track[0], trading_day_low_pe_return-trading_day_high_pe_return])
    except KeyError:
        continue
hml=pd.DataFrame(factor,columns=['date','hml'])

至此，三因子模型需要的数据算是建立起来了，下面将所有的数据整合到一起，代码如下：

factors=smb.merge(hml,on=['date'],how='inner',copy=False)
factors =factors.set_index(['date'])
# 将市值因子整合到一起
factors['capm']=sh
factors['const']=1
# 对每一只股票进行回归，得出资产池内的单个资产的暴露情况
# 假设所有的因子都是统计显著的
from sklearn.linear_model import LinearRegression
factor_loading=[]
for stock_id in sz380return.columns:
    regression_data=factors.copy()
    regression_data[stock_id]=sz380return[stock_id]
    print (stock_id)
    model=LinearRegression(fit_intercept = True).fit(regression_data[['capm','smb','hml']],regression_data[stock_id])
    factor_loading.append ([stock_id]+[model.intercept_]+list (model.coef_))
# 最后整理为DataFrame
factor_loading=pd. DataFrame(factor_loading, columns=['stock_id','alpha','capm','smb','hml'])

假如我们需要构建一个 SML 因子暴露为0.5、CAPM 因子暴露为1.2、HML 因子暴露为0.3的投资组合，实质就是解方程组。

np.dot(Idiosyncratic_exposure.T,weight) = target_exposure

你肯定发现，这个方程组大概率会有无穷多个解，所用的方式一般是求矩阵的广义逆。在实操过程当中，会有很多限定条件来进一步缩小投资组合的范围，代如下：

factor_loading_array=factor_loading[['capm','smb','hml']].values.T
weight=list(np.dot(np.linalg.pinv(factor_loading_array).np.array([1.2,0.5,0.3]).T))

至此，一个FF3因子模型基本复现完成。

因子发掘与论证
一般意义上来讲，所有的因子模型采用的都是如下一个通用流程。
口从各种维度统计论证某个指标的时间序列选股的有效性。包括因子收益是否统计显著为正，其背后的因果关系是怎么样的，在未来是否还会复现，成本收益比如何，是否已经被市场的套利团队填平了收益等。
口利用该指标的历史时间序列构建资产池序列，并跟踪其收益。
口将收益序列作为一个回归项对现有的资产池所有管辖资产进行回归，得出各个资产因子的显著暴露。
口根据基金经理的投资风格、投资目标、风险收益比权衡等因素，确定投资组合的目标因子暴露。
口计算出权重，进行资金分配。

可以发现，其实这里最重要的一个步骤就是发现有效因子。一个因子是否有效，通常意义上必须要满足两个条件。
1）在统计意义上是显著的。

2）其因果关系是可以论证的。前者其实非常容易实现，而后者则相对要难很多。发现因子的过程其传统的做法是通过经济学论证或者是基金经理长期多年在股票市场上挖掘出来的因子。而这些方法发掘因子的效率极其低下。近年来，发现因子的方法出现了一些新的模式。通过各种数据的排列组合，以及模型的不断尝试，挖掘出在统计意义上有效的因子，之后再交给资深的基金经理进行论证和判断，选取能够在因果逻辑上行得通的因子推动投资组合建立。目前市面上已经有团队在用类似的方法进行尝试。可以想见的是，传统的技术分析带来的收益回报将会被这些团队全部攫取，市场将会变得更加有效。

单因子有效性分析 alphalens

alphalens是一个用于进行单因子分析的开源项目，是由国外的在线量化平台quantopian 开发的。使用alphalens，我们可以对单因子的有效性进行全面的分析。
使用alphalens，用户只需要做两件事情。一是数据的预处理，要将数据处理成alphalens 需要的数据格式；二是读懂 alphalens的计算结果和相应表图。

数据预处理

我们先来进行数据预处理操作。数据预处理的核心函数如下：

alphalens.utils.get_clean_factor_and_forward_returns(factor, prices, groupby=None,\
        by_group=False, quantiles=5, bins=None, periods=(1, 5, 10), filter_zscore=20, groupby_labels=None)

这个函数会将输人的数据整合成alphalens 需要的形式。用户需要做的就是将参数的数据准备好，作为输人。
其中，比较常用的有factor、prices（必须要是用户定义的）、groupby、groupby_labels （用于对股票的分类进行分析），一般是用行业来进行分类，类别可以自行定义。periods定义了分析因子和未来多少天的收益率的关系。默认是1、5、10，也就是会分析因子和未来1天、5天、10天的收益率的关系。
数据来源，由于需要用到行业数据，因此我们使用的是开源的数据接口tushare和akShare，两者须同时使用。
首先，我们需要获取股票列表。tuShare提供了接口，用于获取沪深A 股的股票代码和相应的行业分类，代码如下：

import tushare as ts
pro = ts.pro_api('fdf059e3fd18ba53290c4907562f871fc598b37ac78f2536859003f3')
#查询当前所有正常上市交易的股票列表
#您每小时最多访问该接口1次
data = pro.query('stock_basic', exchange='', list_status='L', fields='ts_code,symbol,name,area,industry,list_date')

结果如下：

data

相比于akshare就不全面：

为了简化问题，我们只随机选取其中100只股票进行分析，在数据整合函数中，不仅要用到行业名称，还需要为每个行业生成相应的ID号，在这里我们自己生成行业的ID号。代码如下：

import random
import pandas as pd
import numpy as np
random.seed(123)  # 设置随机数种子为123

# 创建随机整数序列,不要把范围弄太大，随机生成去取数据，好多都是新股没有历史数据
s = [random.randint(1, 2000) for _ in range(100)]

# 使用s作为df的行索引提取数据
result = data.loc[s]

result = result[['symbol','industry']]
result = result.sort_values('symbol')
# print(result)


# 根据行业名称生成行业对应的ID号
result['industry_name']=result['industry']
industry_name = result.industry_name.unique()
industry_id = range(0,len(industry_name))
# 在result 里添加一列行业对应的ID
sec_names = dict(zip(industry_id, industry_name))
sec_names_rev = dict(zip(industry_name, industry_id))
result['industry_id'] = result['industry_name'].map(sec_names_rev)
# 生成 code 和与行业代码对应的字典
code_sec = dict (zip(result.symbol, result.industry_id))
print(result)

结果如图：

其中code_sec如图：是字典

sec_names也是字典：

接下来，我们获取每只股票的行情数据。使用akShare获取数据的时候，股票如果停牌，那么相应日期的数据就不会存在。为了对齐交易日期，下面我们使用沪深300指数的交易日期作为所有股票的索引基准，代码如下：
＃由于有的股票在某些交易日不交易，导致要提取的数据提取不到
＃所以这里使用沪深300的数据作为交易日的标准

辅助函数：

def gp_type_szsh(gp):
        if code.find('60',0,3)==0:
            gp_type='sh'
        elif code.find('688',0,4)==0:
            gp_type='sh'
        elif code.find('689',0,4)==0:
            gp_type='sh'
        elif code.find('900',0,4)==0:
            gp_type='sh'
        elif code.find('00',0,3)==0:
            gp_type='sz'
        elif code.find('300',0,4)==0:
            gp_type='sz'
        elif code.find('301',0,4)==0:
            gp_type='sz'
        elif code.find('200',0,4)==0:
            gp_type='sz'
        elif code.find('8',0,1)==0:
            gp_type='bj'
        elif code.find('430',0,4)==0:
            gp_type='bj'
        return gp_type+gp

import akshare as ak
code='000001'
start_date='2020-01-01'
end_date='2023-09-29'

df = ak.index_zh_a_hist(symbol=code, period="daily", start_date=start_date, end_date=end_date)
# print(index_zh_a_hist_df)
df = df[['日期','开盘','最高','最低','收盘']]
df = df.rename(columns={'日期': 'date','开盘': 'open','最高': 'high','最低': 'low','收盘': 'close'})
df=df.set_index('date')
df[code]=df.open
df=df[[code]]
# print(df)

# 取所有股票的数据，并与沪深300数据的日期进行对齐
for code in result.symbol:
    stock_code = gp_type_szsh(code)
    stock_df = ak.stock_zh_a_daily(symbol=stock_code, start_date=start_date, end_date=end_date)
    stock_df=stock_df.set_index('date')
    df[code]=stock_df.open
# 将index 转换为datetime 格式（从TuShare 导出的数据date是字符串格式）
df.index=pd.to_datetime(df.index)

#提出指数数据
del df['000001']
df

结果如图：df行为日期，列为股票代码

这里为了进行说明，我们使用未来5天的收益率作为因子进行分析。未来5天的收益率用于预测未来5天的收益率，当然是百分之百的准确，而且未来5天的收益率会与第1天、第10天的收益率有很强的相关性。所以在表现上，这会是一个很强的因子（当然现实中，我们不可能知道未来5天的收益率，这里只是举例说明，并没有实际的意义），代码如下：
＃为了更有效地演示，这里我们使用未来5天的收益率作为预测因子
# 这个因子由于加入了未来函数，所以会有很强的预测效果

lookahead_bias_days=5
predictive_factor = df.pct_change(lookahead_bias_days)
predictive_factor = predictive_factor.shift(-lookahead_bias_days)
predictive_factor = predictive_factor.stack()
predictive_factor.index = predictive_factor.index.set_names(['datet','asset'])
predictive_factor.head()

predictive_factor是双索引的Series类型。两个索引分别是日期和对应的资产代码，对应的数值是 factor值，结果为：

数据准备好了后，调用整合函数进行处理：

import alphalens
# 将数据整合为alphalens所需要的格式
pricing = df
factor_data = alphalens.utils.get_clean_factor_and_forward_returns (predictive_factor, pricing, quantiles = 5, bins = None,groupby = code_sec, groupby_labels = sec_names)
factor_data.head()

结果如图：

额，这里数据有问题，找了几天没找到问题所在，说是矩阵行列长度不符合，这里进行不下去后面就无法进行分析。

这是数据整合后的格式，是DataFrame类型，日期和资产代码作为双重索引。列1、5、10分别代表未来1、5、10天的收益率，factor是因子值，group是分类，factor_quantile是将因子从小到大划分区间进行的分类，这里由于参数quantiles=5，所以是分为5类。1代表因子是处于最小的那一部分因子中，5代表因子处理最大的那一类，其余的类似。
完成了数据整合之后，数据准备工作就完成了。剩下的代码很简单，直接调用相应的函数就可以进行分析了。

收益率分析

最基础的分析就是查看不同大小（不同分位数）的因子和未来收益率的相关性，代码如下：

mean_return_by_q, std_err_by_q = alphalens.performance.mean_return_by_quantile(factor_data, by_group=False)
mean_return_by_q.head()

结果如图：--

这里计算出了每个分位数的因子所对应的收益率（平均值），代码如下：

alphalens.plotting.plot_quantile_returns_bar(mean_return_by_q)

换成图会更直观，每个分位的因子所对应的收益率如图所示：--

可以看到的是，随着因子的增大，未来的收益率也会增加，说明因子和收益率具有很强的相关性，可能是一个不错的因子。
alphalens 的强大之处在于可以多方位审视一个因子的有效性。除了上面提到的最基础的因子分位数和收益率的关系之外，还提供了其他的方法来进行检测。
比如，绘制每个调仓期最高因子和最低因子收益率的差值，代码如下：

mean_return_by_q_daily, std_err= alphalens.performance.mean_return_by_quantile(factor_data, by_date=True)
quant_return_spread, std_err_spread = alphalens.performance.compute_mean_returns_spread (mean_return_by_q_daily, upper_quant=5,lower_quant=1,std_err=std_err)
alphalens.plotting.plot_mean_quantile_returns_spread_time_series (quant_return_spread, std_err_spread)

下图是绘制出来的其中一幅图：--

上图是针对未来1天的收益率，绿色的线（上下波动的密集波线）代表最高的因子收益率和最低因子收益率的差值。如果一个因子是有效的，那么我们应当期望这个差值会一直稳定地大于0（当然，对于反向因子，这个差值应该一直稳定地小于0)。总之，这个差值应该是比较稳定的，而不是时而大于0，时而小于0。通过上图我们可以看到，大部分时间绿色的线都在0以上，说明因子在时间维度上是比较稳定的。橙色的线（中间比较平缓的曲线）是绿色线的移动平均线，移动平均线是为了便于观察因子有效性的趋势。
下面求取不同分位数因子的累计净值，绘制结果如图所示：--

alphalens.plotting.plot_cumulative_returns_by_quantile(mean_return_by_q_daily)

上图绘制了不同分位数因子的累计净值。一个好的因子，在累计收益率上，应该出现较大的分化。在上图中，不同分位数因子的累计净值确实出现了很大的分化。
实际应用调用一个函数，就能给出以上所有的收益率分析的结果报表，代码如下：

alphalens.tears.create_returns_tear_sheet (factor_data)

信息系数分析

信息系数（Information Coefficient Analysis）是衡量因子有效性的另外一个角度。信息系数与相关系数比较相似，都是用于衡量两个变量的线性关系。信息系数在0到1之间，0表示因子没有任何预测作用，1表示因子有完全的预测作用。信息系数越大，表明因子的预测效果越好。
可以用以下函数计算信息比率：

ic=alphalens.performance.factor_information_coefficient (factor_data)
ic.head()

计算结果如图所示:--

上图中、1、5、10分别代表了因子对于未来1、5、10天收益率的信息系数。可以看到，5天的收益率信息系数是1，因为我们本来就是用5的未来收益率作为因子，所以能够完美预测。同时，对于1天，10天的效果也很明显。
也可以绘制信息系数的图，代码如下：

alphalens.plotting.plot_ic_ts(ic)

绘制的图形分别如下三幅图所示：--  --  --

通过上面的三幅图，我们可以看到信息系数随时间变化的表现。对于长期的。一个好的因子，信息系数应该比较高，而且波动应该比较小。这就说明这个因子是有效且也可以观察信息系数的分布，代码如下：

alphalens.plotting.plot_ic_hist(ic)

绘制的信息系数分布图如图所示：--（三个周期三幅图）

从上图中我们可以看到，10天的信息系数比1天的高而且稳定。

只看均值有时候也会带来误解。比如，如果有一个极端大的值，那么它很可能就会拉高整体的平均值。这个时候就需要用Q-Q图（quantile-quantile plot）来排除这个可能性。Q-Q图主要是比较信息系数的分布和正态分布的区别。绘制Q-Q图的代码如下：

alphalens.plotting.plot_ic_qq(ic)

绘制结果如图所示：--（三个周期三幅图）

可以看到，1和10的Q-Q图和红线比较接近，说明分布是类似于正太分布的，说明信息系数平均值好，并不是由于几个极端的值造成的。
我们也可以按月份来观察信息系数，代码如下：

mean_monthly_ic=alphalens.performance.mean_information_coefficient(factor_data,by_time='M')
mean_monthly_ic.head()

输出结果如图所示：--

绘制每个月的信息系数表现图，代码如下：

alphalens.plotting.plot_monthly_ic_heatmap(mean_monthly_ic)

信息系数表现图如图所示：--

从上图中，我们可以看到每个月的信息系数的表现。

当然alphalens也提供了所有信息系数分析的报表函数，代码如下：

alphalens.tears.create information_tear_sheet(factor_data)

除了收益率和信息系数分析，alphalens还提供了换手率和按行业分类的分析。这里不再过多介绍，请自行查阅官方文档。我后续要把这里的问题查资料解决。

财务因子为什么不好用

股票量化模型，最流行的就是多因子模型。多因子模型是从Fama-French三因子模型衍生而来的，基本框架从未变过。
因子有很多种，比如动量因子、估值因子、盈利因子、行业因子，等等。最大的好处是，可以用统一的框架解释所有的事情。缺点也很明显，实际研究发现，真有效的可能就那么几个，比如动量、市值、账面市值比之类的因子。
大部分财务因子，要么就是效果不好（统计显著性不明显），要么就是因为共线性被删掉了。研究多了会发现，忽略财务指标，深挖技术指标，实际产出可能会更高。
比如World Quant的101 Alpha因子，全是技术因子。再比如，Two Sigma两年前在Kaggle上举办过一项挑战，放出了积累了十几年的上百个因子，主要有44个技术指标因子和63个基本面因子。结果一通操作下来，发现最显著的还是技术因子。
局面就很诡异了。量化界研究下来，技术因子比基本面因子有效。传统投资界又看不起技术分析。无论是写研报还是做投资，大家都只关心财务数据。
按理说，财务数据的信息量应该远大于技术指标，为什么就是不好呢？后来想明白了，原因很简单：量化主要依据统计信息，无论什么指标，都要先进行回归和检验。
然而，财务指标领域的知识极多，样本又少，还呈现各种非线性，完全是统计模型的克星。文章来源地址https://www.toymoban.com/news/detail-728899.html

到了这里，关于量化交易全流程（六）（待完善补充）的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！