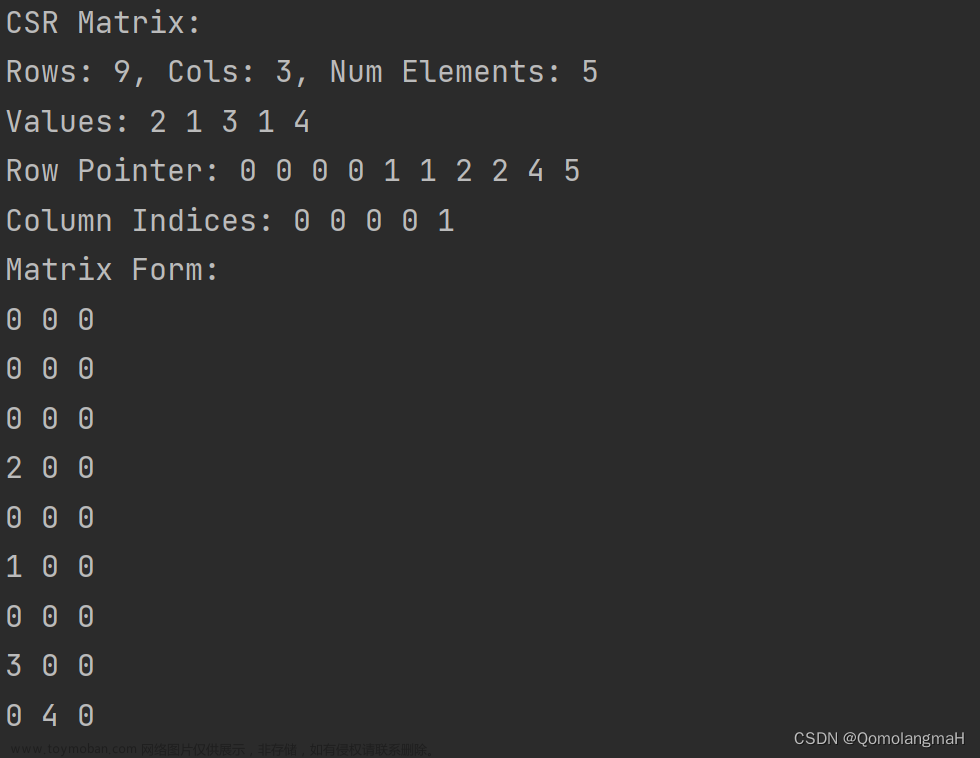
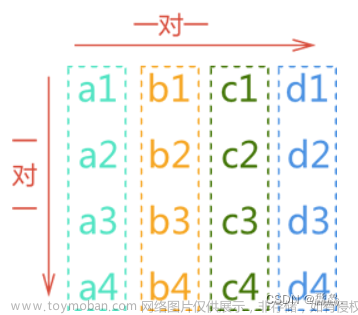
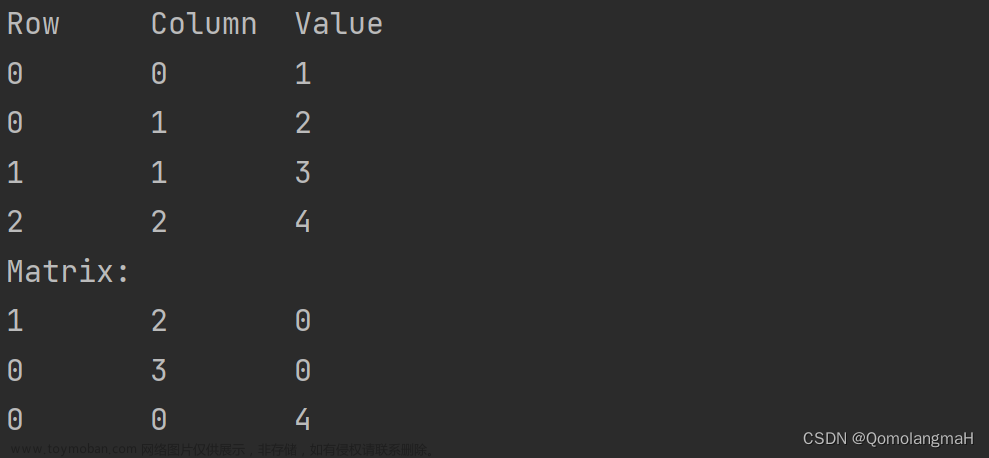
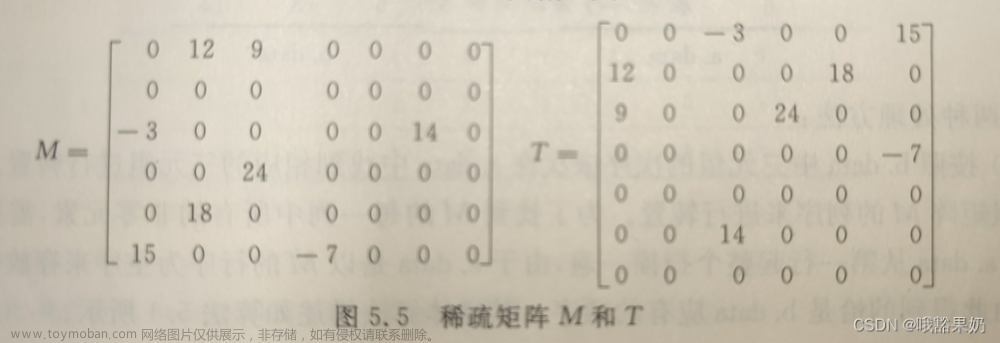
王道书中给出定义如下:
书中没有给出具体的推导过程,在CSDN上也没搜到,因此我来发一篇(哈哈哈哈哈
推导过程如下:
首先除去第一行。
从第二行开始,当矩阵的下标为(i,j)的时候:
- 前面一定会有第一行的2个
- 会有从第2行开始到第i-1行的每行3个,因此是3(i-1-2+1)=3(i-2)
- j的取值是从i-1到i+1,因此第i行的第j个数在本行的次序是:j-(i-1)+1=j-i+2.
综上, a i j a_{ij} aij在所有不为0的数中的次序就是2+3(i-2)+j-i+2=2i+j-2
数组下标如果从0开始,那么它在压缩后的数组中的下标就是次序减1,也就是2i+j-3
然后把第一行带入演算,发现也是ok的,因此答案就是2i+j-3。
数组向矩阵的转换可以通过这个式子反推。假设数组中下标为k的元素,我们要找到它的i和j。
在三对角矩阵中,我们有: i − 1 ≤ j ≤ i + 1 i-1 \leq j \leq i+1 i−1≤j≤i+1因此就有: 3 i − 4 ≤ k ≤ 3 i − 2 3i-4\leq k \leq 3i-2 3i−4≤k≤3i−2
也就是: 3 ( i − 1 ) ≤ k + 1 ≤ 3 i − 2 3(i-1)\leq k+1\leq 3i-2 3(i−1)≤k+1≤3i−2
我们可以通过向下取整函数得到准确的 i − 1 i-1 i−1,即 ⌊ k + 1 3 ⌋ = i − 1 \lfloor \frac{k+1}{3}\rfloor=i-1 ⌊3k+1⌋=i−1也就是 i = ⌊ k + 1 3 ⌋ + 1 i=\lfloor \frac{k+1}{3}\rfloor+1 i=⌊3k+1⌋+1.文章来源:https://www.toymoban.com/news/detail-728901.html
有了i之后,j就很好求了,带入 k = 2 i + j − 3 k=2i+j-3 k=2i+j−3就能得到j。文章来源地址https://www.toymoban.com/news/detail-728901.html
到了这里,关于【数据结构】三对角矩阵(带状矩阵)的压缩 数组下标转换的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!