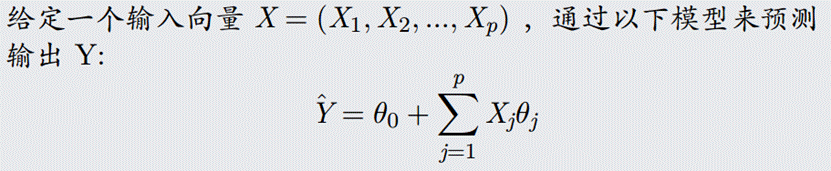一 线性回归
线性回归是机器学习中 有监督机器学习 下的一种算法。 回归问题主要关注的是因变量(需要预测的值,可以是一个也可以是多个)和一个或多个数值型的自变量(预测变量)之间的关系。
- 需要预测的值:即目标变量,target,y,连续值预测变量。
- 影响目标变量的因素: ... ,可以是连续值也可以是离散值。
- 因变量和自变量之间的关系:即模型,model,是我们要求解的。
1.1 简单线性回归
前面提到过,算法说白了就是公式,简单线性回归属于一个算法,它所对应的公式。
这个公式中,y 是目标变量即未来要预测的值,x 是影响 y 的因素,w,b 是公式上的参数即要求的模型。其实 b 就是咱们的截距,w 是斜率嘛! 所以很明显如果模型求出来了,未来影响 y 值的未知数就是一个 x 值,也可以说影响 y 值 的因素只有一个,所以这是就叫简单线性回归的原因。
1.2 最优解
- Actual value: 真实值,一般使用 y 表示。
- Predicted value: 预测值,是把已知的 x 带入到公式里面和猜出来的参数 w,b 计算得到的,一般使用 表示。
- Error: 误差,预测值和真实值的差距,一般使用 表示。
- 最优解: 尽可能的找到一个模型使得整体的 误差最小,整体的误差通常叫做损失 Loss。
- Loss: 整体的误差,Loss 通过损失函数 Loss function 计算得到。
1.3 多元线性回归
现实生活中,往往影响结果 y 的因素不止一个,这时 x 就从一个变成了 n 个,.....同时简单线性回归的公式也就不在适用了。多元线性回归公式如下:
使用向量来表示:
二 高斯函数
2.1 正太分布
正态分布(Normal Distribution),也被称为高斯分布(Gaussian Distribution),正态分布在实际应用中非常有用,因为许多自然现象和人类行为都近似遵循正态分布。例如,身高、体重、智商、测量误差等都可以用正态分布来描述。在统计分析中,许多参数估计和假设检验方法都基于正态分布的假设。在统计建模中,通常默认每次线性模型计算的误差与正确值的误差符合正态分布。基于这一假设,可以通过计算使误差最小的正态分布值来估算线性模型的权重。这种方法有助于拟合模型以更好地解释数据和进行预测。主要特点:
-
对称性:正态分布是一个对称分布,其均值、中位数和众数都位于分布的中心,也就是分布的峰值。
-
集中趋势:正态分布具有集中趋势,数据点更有可能接近均值,而在离均值越远的地方概率逐渐减小。
-
定义性:正态分布由两个参数决定,均值(μ)和方差(σ^2),这些参数决定了分布的中心和分散度。
-
标准正态分布:当均值为0,方差为1时,正态分布被称为标准正态分布(Standard Normal Distribution)。标准正态分布的概率密度函数可以用标准正态分布表来查找。
-
经典的钟形曲线:正态分布的概率密度函数呈现出典型的钟形曲线,两侧尾部逐渐减小,且在均值处达到峰值。
正态分布的概率密度函数(Probability Density Function)为:

2.2 误差分析
假定所有的样本的误差都是独立的,有上下的震荡,震荡认为是随机变量,足够多的随机变量叠加之后形成的分布,它服从的就是正态分布,因为它是正常状态下的分布,也就是高斯分布!均值是某一个值,方差是某一个值。 方差我们先不管,均值我们总有办法让它去等于零 0 的,因为我们这里是有截距b, 所有误差我们就可以认为是独立分布的,1<=i<=n,服从均值为 0,方差为某定值的高斯分布。机器学习中我们假设误差符合均值为0,方差为定值的正态分布!!!
正太分布公式:
随着参数μ和σ变化,概率分布也产生变化。 下面重要的步骤来了,我们要把一组数据误差出现的总似然,也就是一组数据之所以对应误差出现的 整体可能性 表达出来了,因为数据的误差我们假设服从一个高斯分布,并且通过截距项来平移整体分布的位置从而使得μ=0,所以样本的误差我们可以表达其概率密度函数的值如下:
误差正太分布,简化去掉均值 μ:
2.3 误差总似然
累乘问题:
根据前面公式 可以推导出来如下公式:
公式中的未知变量就是 ,即方程的系数,系数包含截距~如果,把上面当成一个方程,就是概率P关于W的方程!其余符号,都是常量!
通过,求对数把累乘问题,转变为累加问题:
简化:
上面公式是最大似然求对数后的变形,其中 都是常量,而 肯定大于零!上面求最大值问题,即可转变为如下求最小值问题:
L代表Loss,表示损失函数,损失函数越小,那么上面最大似然就越大~
有的书本上公式,也可以这样写,用表示一个意思,的角色就是W:
进一步推导:
其中:
表示全部数据,是矩阵,X表示多个数据,进行矩阵乘法时,放在前面;
表示第i个数据,是向量,所以进行乘法时,其中一方需要转置。
因为最大似然公式中有个负号,所以最大总似然变成了最小化负号后面的部分。 到这里,我们就已经推导出来了 MSE 损失函数 ,从公式我们也可以看出来 MSE 名字的来 历,mean squared error,上式也叫做 最小二乘法!
这种最小二乘法估计,其实我们就可以认为,假定了误差服从正太分布,认为样本误差的出现是随机的,独立的,使用最大似然估计思想,利用损失函数最小化 MSE 就能求出最优解!所以反过来说,如果我们的数据误差不是互相独立的,或者不是随机出现的,那么就不适合去假设为正太分布,就不能去用正太分布的概率密度函数带入到总似然的函数中,故而就不能用 MSE 作为损失函数去求解最优解了!所以最小二乘法不是万能的~
还有譬如假设误差服从泊松分布,或其他分布那就得用其他分布的概率密度函数去推导出损失函数了。
所以有时我们也可以把线性回归看成是广义线性回归。比如,逻辑回归,泊松回归都属于广义线性回归的一种,这里我们线性回归可以说是最小二乘线性回归。
三 正规方程
3.1 最小二乘法矩阵表示
最小二乘法可以将误差方程转化为有确定解的代数方程组(其方程式数目正好等于未知数的个数),从而可求解出这些未知参数。这个有确定解的代数方程组称为最小二乘法估计的正规方程。公式如下:
或者
最小二乘法公式如下:
使用矩阵表示:
3.2 矩阵转置公式与求导公式:

3.2.1 公式展开
3.2.2 求导
3.2.3 推导
令导数
3.2.4 使用逆矩阵进行转化
公式推导结束:

四 使用代码计算
4.1 简单线性回归
4.1.1 数据生成
import numpy as np
import matplotlib.pyplot as plt
# 转化为矩阵
X = np.linspace(0, 10, num=30).reshape(-1, 1)
# 斜率和截距,随机生成
w = np.random.randint(1,5,size = 1)
b = np.random.randint(1,10,size = 1)
# 根据一元一次方程计算目标值y,并加上“噪声”,数据有上下波动~
y = X * w + b + np.random.randn(30,1)
print(f'w:{w}, b:{b}') # w:[4], b:[1]
plt.scatter(X,y) # "scatter" 表示"散点"
4.1.2 正规方程求解
求导公式:
np.concatenate 是 NumPy 库中用于数组拼接和连接的函数:

plt.scatter(X,y)
# 重新构造X, 不相当于截距,给b一个权重1,方便矩阵计算
"""np.concatenate 是 NumPy 库中用于数组拼接和连接的函数"""
X = np.concatenate([X, np.full(shape = (30, 1), fill_value=1)], axis=1)
# 正规方程求解
""""
1 np.linalg.inv 是 NumPy 中的线性代数函数,用于计算矩阵的逆
2 np.dot() 计算了它们的矩阵乘法。
3 使用 .T 属性来获取矩阵的转置
4 .round(2) 是 Python 中用于四舍五入数字到指定小数位数的方法。
"""
a = np.linalg.inv(X.T.dot(X)).dot(X.T).dot(y).round(2)
print(f'查看正规方程求解结果:', a) # [[3.98] [3.88]]
plt.plot(X[:, 0], X.dot(a), color='green')
4.2 多元线性回归求解
求解公式:θ = np.linalg.inv(X.T.dot(X)).dot(X.T).dot(y).round(2)文章来源:https://www.toymoban.com/news/detail-730644.html
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d.axes3d import Axes3D # 绘制三维图像
# 转化成矩阵
x1 = np.random.randint(-150,150,size = (300,1))
x2 = np.random.randint(0,300,size = (300,1))
# 斜率和截距,随机生成
w = np.random.randint(1,5,size = 2)
b = np.random.randint(1,10,size = 1)
# 根据二元一次方程计算目标值y,并加上“噪声”,数据有上下波动~
y = x1 * w[0] + x2 * w[1] + b + np.random.randn(300,1)
fig = plt.figure(figsize=(15, 12))
ax = fig.add_subplot(projection='3d')
ax.scatter(x1,x2,y) # 三维散点图
ax.view_init(elev=10, azim=-20) # 调整视角
# 重新构造X,将x1、x2以及截距b,相当于系数w0,前面统一乘以1进行数据合并
X = np.concatenate([x1,x2,np.full(shape = (300,1),fill_value=1)],axis = 1)
w = np.concatenate([w,b])
# 正规方程求解
θ = np.linalg.inv(X.T.dot(X)).dot(X.T).dot(y).round(2) # 计算公式
print('二元一次方程真实的斜率和截距是:',w)
print('通过正规方程求解的斜率和截距是:',θ.reshape(-1))
# # 根据求解的斜率和截距绘制线性回归线型图
x = np.linspace(-150,150,100)
y = np.linspace(0,300,100)
z = x * θ[0] + y * θ[1] + θ[2]
ax.plot(x,y,z ,color = 'red') 文章来源地址https://www.toymoban.com/news/detail-730644.html
文章来源地址https://www.toymoban.com/news/detail-730644.html
到了这里,关于关于线性模型的底层逻辑解读 (机器学习 细读01)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!