LeetCode 509 斐波那契数（动态规划）-Toy模板网

这篇具有很好参考价值的文章主要介绍了LeetCode 509 斐波那契数（动态规划）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

509. 斐波那契数 - 力扣（LeetCode）

斐波那契数 （通常用 F(n) 表示）形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始，后面的每一项数字都是前面两项数字的和。也就是：

示例 1：

输入：n = 2
输出：1
解释：F(2) = F(1) + F(0) = 1 + 0 = 1

示例 2：
输入：n = 3
输出：2
解释：F(3) = F(2) + F(1) = 1 + 1 = 2

示例 3：
输入：n = 4
输出：3
解释：F(4) = F(3) + F(2) = 2 + 1 = 3
F(0) = 0，F(1) = 1
F(n) = F(n - 1) + F(n - 2)，其中 n > 1

给定 n ，请计算 F(n) 。

【思路】动态规划

动规五部曲：

1.确定dp数组以及下标的含义

dp[i]的定义为：第i个数的斐波那契数值是dp[i]

2.确定递推公式

状态转移方式 dp[i] = dp[i-1] + dp[i-2];

3.dp数组如何初始化

dp[0] = 0;
dp[1] = 1;

4.确定遍历顺序

从递归公式dp[i] = dp[i-1] + dp[i-2];中可以看出，dp[i]是依赖dp[i-1] 和 dp[i-2]，那么遍历的顺序一定是从前到后遍历的

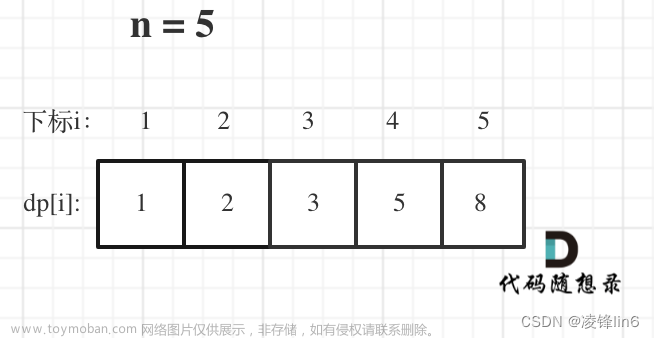
5.举例推导dp数组

i: 0 1 2 3 4 5 6 7

dp[i]: 0 1 1 2 3 5 8 11

动态递推公式 : dp[i] = dp[i-1] + dp[i-2];

class Solution {
public:
    // 方法一：递归
    // 缺点:效率低
    int fib(int n) {
        if(n < 2) return n;
        return fib(n-1) + fib(n-2);
    }

    // 方法二
    // ① 动态规划  ② 时间复杂度:O(n) 空间复杂度:O(n)
    int fib(int n) { 
        if(n <= 1) return n; 
        vector<int> dp(n+1);
        dp[0] = 0;dp[1] = 1;
        for(int i = 2; i <= n; i++) {
            dp[i] = dp[i-1] + dp[i-2];
        }
        return dp[n];
    }

    // 方法二 进一步优化
    // ① 动态规划  ② 时间复杂度:O(n) 空间复杂度:O(1)
    int fib(int n) { 
        if(n <= 1) return n; 
        int dp[2];
        dp[0] = 0;dp[1] = 1;
        for(int i = 2; i <= n; i++) {
            int sum = dp[0] + dp[1];
            dp[0] = dp[1];
            dp[1] = sum;
        }
        return dp[1];
    }
};

本题和爬楼梯类似，可以看我的往期文章：

LeetCode 509 斐波那契数（动态规划）,动态规划,leetCode,leetcode,斐波那契,动态规划,维护两个数值

leetCode 746. 使用最小花费爬楼梯 + 记忆化搜索 + 递推 + 动态规划 + 空间优化-CSDN博客https://heheda.blog.csdn.net/article/details/134192825?spm=1001.2014.3001.5502LeetCode 70.爬楼梯 + 记忆化搜索 + 递推 + 动态规划 + 空间优化-CSDN博客https://heheda.blog.csdn.net/article/details/134192204?spm=1001.2014.3001.5502参考和推荐文章：

代码随想录 (programmercarl.com)https://programmercarl.com/0509.%E6%96%90%E6%B3%A2%E9%82%A3%E5%A5%91%E6%95%B0.html#%E6%80%9D%E8%B7%AF文章来源地址https://www.toymoban.com/news/detail-731049.html

到了这里，关于LeetCode 509 斐波那契数（动态规划）的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！