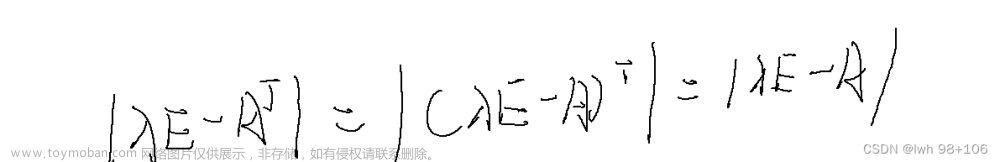定义 1 设 V V V 是一个非空集合, R \R R 为实数域。如果在 V V V 中定义了一个 加法,即对于任意两个元素 α , β ∈ V \boldsymbol{\alpha}, \boldsymbol{\beta} \in V α,β∈V,总有唯一的一个元素 γ ∈ V \boldsymbol{\gamma} \in V γ∈V 与之对应,称为 α \boldsymbol{\alpha} α 与 β \boldsymbol{\beta} β 的 和,记作 γ = α + β \boldsymbol{\gamma} = \boldsymbol{\alpha} + \boldsymbol{\beta} γ=α+β;在 V V V 中又定义了一个数与元素的乘法(简称 数乘),即对于任一数 λ ∈ R \lambda \in \R λ∈R 与任一元素 α ∈ V \boldsymbol{\alpha} \in V α∈V,总有唯一的一个元素 δ = λ α \boldsymbol{\delta} = \lambda \boldsymbol{\alpha} δ=λα,并且这两种运算满足以下八条运算规律(设 α , β , γ ∈ V \boldsymbol{\alpha},\boldsymbol{\beta},\boldsymbol{\gamma} \in V α,β,γ∈V、 λ ∈ R \lambda \in \R λ∈R):
- α + β = β + α \boldsymbol{\alpha} + \boldsymbol{\beta} = \boldsymbol{\beta} + \boldsymbol{\alpha} α+β=β+α;
- ( α + β ) + γ = α + ( β + γ ) (\boldsymbol{\alpha} + \boldsymbol{\beta}) + \boldsymbol{\gamma} = \boldsymbol{\alpha} + (\boldsymbol{\beta} + \boldsymbol{\gamma}) (α+β)+γ=α+(β+γ);
- 在 V V V 中存在 零元素 0 \boldsymbol{0} 0,对任何 α ∈ V \boldsymbol{\alpha} \in V α∈V,都有 α + 0 = α \boldsymbol{\alpha} + \boldsymbol{0} = \boldsymbol{\alpha} α+0=α;
- 对任何 α ∈ V \boldsymbol{\alpha} \in V α∈V,都有 α \boldsymbol{\alpha} α 的 负元素 β ∈ V \boldsymbol{\beta} \in V β∈V,使 α + β = 0 \boldsymbol{\alpha} + \boldsymbol{\beta} = \boldsymbol{0} α+β=0;
- 1 α = α 1 \boldsymbol{\alpha} = \boldsymbol{\alpha} 1α=α;
- λ ( μ α ) = ( λ μ ) α \lambda (\mu \boldsymbol{\alpha}) = (\lambda \mu) \boldsymbol{\alpha} λ(μα)=(λμ)α;
- ( λ + μ ) α = λ α + μ α (\lambda + \mu) \boldsymbol{\alpha} = \lambda \boldsymbol{\alpha} + \mu \boldsymbol{\alpha} (λ+μ)α=λα+μα;
- λ ( α + β ) = λ α + λ β \lambda (\boldsymbol{\alpha} + \boldsymbol{\beta}) = \lambda \boldsymbol{\alpha} + \lambda \boldsymbol{\beta} λ(α+β)=λα+λβ。
那么, V V V 就称为(实数域 R \R R 上的)向量空间(或 线性空间), V V V 中的元素无论其本来的性质如何,统称为(实)向量。
简言之,凡满足上述八条规律的加法及数乘运算,就称为 线性运算;凡定义了线性运算的集合,就称为 向量空间,其中的元素就称为向量。
向量空间的概念是集合与运算两者的结合。一般来说,同一个集合,若定义两种不同的线性运算,就构成不同的向量空间;若定义的运算不是线性运算,就不能构成想来那个空间。
向量空间具有如下特征:
性质 1 零向量是唯一的。
证明见 “【证明】线性空间的基本性质”。
性质 2 任一向量的负向量是唯一的, α \boldsymbol{\alpha} α 的负向量记作 − α - \boldsymbol{\alpha} −α。
证明见 “【证明】线性空间的基本性质”。
性质 3 0 α = 0 0 \boldsymbol{\alpha} = \boldsymbol{0} 0α=0。
证明见 “【证明】线性空间的基本性质”。
性质 4 ( − 1 ) α = − α (-1)\boldsymbol{\alpha} = - \boldsymbol{\alpha} (−1)α=−α。
证明见 “【证明】线性空间的基本性质”。
性质 5 λ 0 = 0 \lambda \boldsymbol{0} = \boldsymbol{0} λ0=0。
证明见 “【证明】线性空间的基本性质”。
性质 6 如果 λ α = 0 \lambda \boldsymbol{\alpha} = \boldsymbol{0} λα=0,则 λ = 0 \lambda = 0 λ=0 或 α = 0 \boldsymbol{\alpha} = \boldsymbol{0} α=0。
证明见 “【证明】线性空间的基本性质”。
有子空间的定义如下:
定义 2 设 V V V 是一个线性空间, L L L 是 V V V 的一个非空子集,如果 L L L 对 V V V 中所有定义的加法和数乘两种运算也构成一个线性空间,则称 L L L 为 V V V 的 子空间。
因为 L L L 是 V V V 的一部分, V V V 中的运算对于 L L L 而言,定义 1 中的规律 1、2、5、6、7、8 显然是满足的,因此只要 L L L 对运算封闭且满足定义 1 中的规律 3 和 4 即可。根据定义 1 的性质可知,若 L L L 对运算封闭,则即能满足规律 3 和 4。因此有
定理 1 线性空间 V V V 的非空子集 L L L 构成子空间的充分必要条件是: L L L 对于 V V V 中的线性运算封闭。文章来源:https://www.toymoban.com/news/detail-731120.html
证明 根据定义 1 和定义 2 显然成立。文章来源地址https://www.toymoban.com/news/detail-731120.html
到了这里,关于线性代数|线性空间的定义与性质的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!