目录
前言
基本认知
数字签名
secp256k1
secp256r1
ed25519
ECDSA七宗罪
EdDSA的诞生
参考
前言
基本认知
- secp256r1、secp256k1、ed25519都是签名算法,而且是具体数字算法的实现。
- secp256k1、secp256r1都属于椭圆曲线数字签名算法ECDSA(Elliptic Curve Digital Signature Algorithm)签名的具体实现,只是椭圆曲线函数不同。是由 NIST(National Institute of Standards and Technology)这个组织确定的。
- ed25519属于EdDSA (Edwards-curve Digital Signature Algorithm) 签名算法的具体实现,是由ANFS组织推进的ed25519密钥体系相关进展。
数字签名
- 数字签名的核心是私钥加签、公钥验签;加签是利用私钥对数据进行签名生成签名值,验签是从签名中恢复公钥的过程。
- 数字签名在以太坊中有三种用途。首先,签名证明私钥的所有者,暗示着以太坊账户的所有者,已经授权支付ether或执行合约。其次,授权的证明是_undeniable_(不可否认)。第三,签名证明交易数据在交易签名后没有也不能被任何人修改。
下图是各加密货币采用的签名算法的现状,可见除了想起项目NEO采用还采用spec256r1,多数是spec256k1。

secp256k1
特定的椭圆曲线称为secp256k1,即曲线 y² = x³ + 7 在有限域 (⼜名伽罗瓦域)。

secp256r1
secp256k1和secp256r1都是ECDSA(椭圆曲线数字签名算法)曲线的参数,区别是他们所使用的随机质数不同,目前行业内对于r1算法的安全性存疑。
ed25519
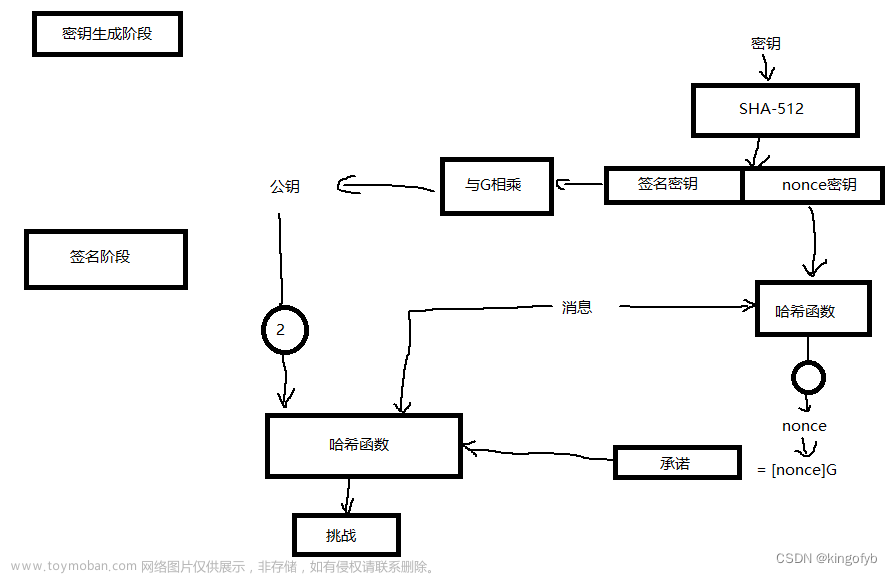
ed25519是基于扭曲爱德华曲线Edwards25519和SHA-512的EdDSA签名机制。
其中Edwards25519曲线是Bernstein等人在2006年提出的蒙哥马利曲线Curve25619的等价变换形式, Curve25519的提出是为了加速ECDH的计算。之所以采用Curve25519的等价变换形式而不是直接利用Curve25519的原因在于ECDH与EdDSA依赖 的点群运算不同,这可以看成是为上层协议适配中层点群运算的经典示例.另外两个曲线在底层有限域的选取中也充分考虑了快速实现与应用编码问题.而Ed25519的签名设计则将ECDSA中常见的随机数问题纳入考量,直接在签名机制内部解决了随机数产生的问题。
curv25519⽤于加密,x25519⽤于密钥交换,ed25519是基于25519曲线的签名。起初⽆⼈问津, 2013 年爱德华·斯诺登曝光棱镜计划后,该算法突然⼤⽕,⼤量软件,如OpemSSH都迅速增加了对 25519 系列的⽀持。
ed25519是⽬前最快的椭圆曲线加密算法,性能远远超过 NIST 系列,⽽且具有⽐ P-256 更⾼的安全性。ed25519是⼀个数字签名算法,签名和验证的性能都极⾼, ⼀个4核 2.4GHz 的 Westmere cpu,每秒可以验证 71000 个签名,安全性极⾼,等价于RSA约3000-bit。
签名过程不依赖随机数⽣成器,不依赖hash函数的防碰撞性,没有时间通道攻击的问题,并且签名很⼩,只有64字节,公钥也很⼩,只有32字节。
BANKIA已成功采用ed25519加密算法,实现链上数据安全传输,ed25519 的安全性在 RSA 2048 与 RSA 4096 之间,性能在数十倍以上。
Ed25519也确实引入了一个在基于secp256k1或者secp256r1的ECDSA签名机制中不存在的问题.一个由于椭圆曲线的余因子(cofactor)不为1导致的问题,使得Monero中可以八花一笔交易(问题已经被修正).secp256k1和secp256r1的余因子为1,所以无需考虑余因子的问题,也不会引发安全问题.而Edwards25519的余因子为8,此时就不得不在应用时将余因子纳入考量的范畴.而余因子为8也部分影响了Ed25519签名机制的设计.
ECDSA七宗罪
-
如果签名过程中随机数值泄露, 则任何知道该随机数值的⼈可以使⽤该随机数产⽣签名值恢复私钥
-
如果同一个用户对两个不同的消息签名时,采用了相同的随机数,则则任何⼈都可以通过两个签名值恢复出私钥
-
如果两个用户执行ECDSA签名时采用了相同的随机数,则两人中的任何一方可以推算出另一方的私钥
-
如果相同的私钥和随机数被同时用于ECDSA签名和Schnorr签名,则任何⼈都能够恢复出私钥
-
ECDSA签名值的可锻造性带来的安全隐患
-
ECDSA签名值的DER编码的不唯一性会带来的安全隐患
-
如果验签时不要求提供被签名的消息,则任何人都可以伪造签名值
EdDSA的诞生
ECDSA安全以及执行效率的问题, 要求在工程手段之外更为深度的改进, 一个自然的方向是重新构建椭圆曲线以及签名机制以便在多个层次上同时改进: 改进底层算术运算加速中层点群运算, 中层点群运算适配上层协议, 并在上层签名机制设计时同时考虑 ECDSA 签名机制的问题与局限性加以避免. EdDSA (Edwards-curve Digital Signature Algorithm) 签名机制是这个研究方向上的成果。文章来源:https://www.toymoban.com/news/detail-731411.html
EdDSA 签名机制是 Bernstein 等人在 2012 年设计的基于爱德华曲线 (Edwards Curves) 的数字签名算法。EdDSA 签名机制是 Schnorr 签名机制的一个变种, 其设计初衷是在不牺牲安全性的前提下提升签名/验签速 度, 并同时解决前述的 ECDSA 在应用方面存在的一些问题.文章来源地址https://www.toymoban.com/news/detail-731411.html
参考
- https://github.com/dalek-cryptography/ed25519-dalek
- https://github.com/jpopesculian/ed25519-dalek-bip32
- https://github.com/jedisct1/rust-ed25519-compact
- https://github.com/w3f/hd-ed25519
- https://github.com/ZenGo-X/multi-party-eddsa
- https://github.com/ZcashFoundation/ed25519-zebra
- https://github.com/RustCrypto/signatures
- Cryptography behind cryptocurrencies
- ECDSA在区块链应用中的七宗罪
- docs/190722-secp256k1-ecdsa-dangers.pdf at master · coinexchain/docs · GitHub
- 维基百科 EdDSA
- ECDSA VS Schnorr signature VS BLS signature
- Extended twisted Edwards curve坐标系及相互转换
- Edwards-Curve Digital Signature Algorithm (EdDSA)
- Cryptography behind top 20 cryptocurrencies
- Ed25519 BIP32 · Issue #6301 · solana-labs/solana · GitHub
- https://smith-mcf.medium.com/solana-vanity-address-using-gpus-5a68ad94d1d4
- 区块链中的Ed25519_mutourend的博客-CSDN博客_ed25519
到了这里,关于一文说明白ECDSA secp256k1 secp256r1 EdDSA ed25519千丝万缕的关系的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!