排序：冒泡排序算法分析-Toy模板网

这篇具有很好参考价值的文章主要介绍了排序：冒泡排序算法分析。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

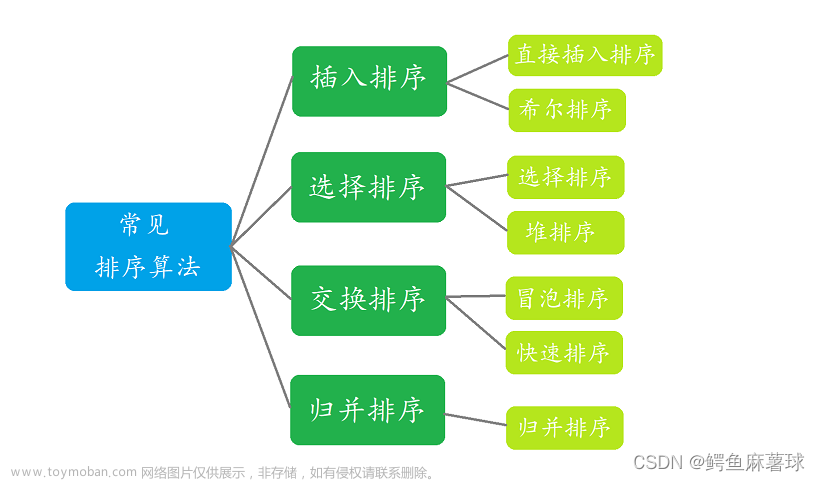
1.交换排序

基于“交换”的排序︰
根据序列中两个元素关键字的比较结果来对换这两个记录在序列中的位置。

交换排序包括冒泡排序和快速排序。

2.冒泡排序

1.算法原理

从后往前(或从前往后)两两比较相邻元素的值，
若为逆序(即 $A [i - 1] > A [i]$ ) ，则交换它们，直到序列比较完。
每一趟排序都可以使一个元素的移动到最终位置，已经确定最终位置的元素在之后的处理中无需再对比。
如果某一趟排序过程中未发生“交换”，则算法可提前结束。
称这样过程为“一趟”冒泡排序。总共需进行n-1趟冒泡。

2.代码实现

从后往前冒，每一次排头得到当前较小值。

//交换
void swap(int &a,int &b){
    int temp = a;
    a = b;
    b = temp;
}
//冒泡排序
void Bubblesort(int A[ ] ,int n){
    for(int i=0; i<n-1 ; i++){
        bool flag=false;//表示本趟冒泡是否发生交换的标志
        for(int j=n-1;j>i;j--)//一趟冒泡过程
            if(A[j-1]>A[j]) {//若为逆序
                swap(A[j - 1], A[j]);//交换
                flag = true;
            }
        if(flag==false)
            return;//本趟遍历后没有发生交换，说明表已经有席t
    }
}