1.概念
2.例题
一、概念
1.提出
层次分析法(Analytic Hierarchy Process,AHP)是一种多标准决策分析方法,用于帮助人们在面对复杂的决策问题时进行定量和定性的比较和评估。它最初由美国运筹学家和管理学家托马斯·萨蒙(Thomas L. Saaty)于20世纪70年代提出,并在后来得到广泛应用。层次分析法在项目选择、供应链管理、风险评估、资源分配等各种决策问题中都有广泛的应用
2.步骤
层次分析法的主要思想是将一个复杂的决策问题分解成多个层次,从总体目标到具体的决策方案,然后通过两两比较不同层次的元素,以确定它们相对于彼此的重要性权重。这些比较通常通过专家判断或调查问卷来完成,然后使用数学方法来计算出最终的权重。
层次分析法的基本步骤:
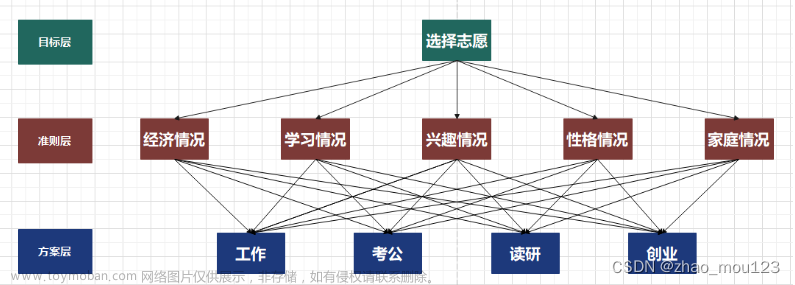
(1)建立层次结构:首先,明确定义决策问题,然后构建一个层次结构,包括目标、准则(criteria)和备选方案(alternatives)等不同层次。
(2)两两比较:专家或决策者需要对每个层次内的元素进行两两比较,以确定它们之间的相对重要性。这些比较通常使用一对一的比较矩阵来表示,其中数值表示相对重要性,例如1代表相等重要性,3代表一个元素比另一个元素重要3倍,以此类推。
(3)构建权重矩阵:基于两两比较的数据,可以构建权重矩阵,用于计算每个元素相对于其他元素的权重。
(4)一致性检验:进行一致性检验,以确保专家的两两比较是一致的。如果比较不一致,需要对比较矩阵进行调整。
(5)计算权重:使用一致性检验通过的权重矩阵来计算每个元素的权重。
(6)**综合评估:**将各个层次的权重综合起来,以得出最终的评估结果,通常是在备选方案层次上。
(7)敏感性分析:进行敏感性分析,评估权重的变化对最终结果的影响,以确定决策的稳定性。
二、例题
例 1 假期旅游有 P1、 P2 、 P3 3 个旅游胜地供你选择,试确定一个最佳地点。
根据诸如景色、费用、居住、饮食和旅途条件等一些准则去反复比较 3 个侯选地点。可以建立如图 1 的层次结构模型。

例 2 挑选合适的工作。经双方恳谈,已有三个单位表示愿意录用某毕业生。
根据已有信息建立了一个层次结构模型,如图 2 所示。





解一 Matlab 程序如下文章来源:https://www.toymoban.com/news/detail-731874.html
clc,clear
fid=fopen('txt3.txt','r');
n1=6;n2=3;
a=[];
for i=1:n1
tmp=str2num(fgetl(fid));
a=[a;tmp]; %读准则层判断矩阵
end
for i=1:n1
str1=char(['b',int2str(i),'=[];']);
str2=char(['b',int2str(i),'=[b',int2str(i),';tmp];']);
eval(str1);
for j=1:n2
tmp=str2num(fgetl(fid));
eval(str2); %读方案层的判断矩阵
end
end
ri=[0,0,0.58,0.90,1.12,1.24,1.32,1.41,1.45]; %一致性指标
[x,y]=eig(a);
lamda=max(diag(y));
num=find(diag(y)==lamda);
w0=x(:,num)/sum(x(:,num));
cr0=(lamda-n1)/(n1-1)/ri(n1)
for i=1:n1
[x,y]=eig(eval(char(['b',int2str(i)])));
lamda=max(diag(y));
num=find(diag(y)==lamda);
w1(:,i)=x(:,num)/sum(x(:,num));
cr1(i)=(lamda-n2)/(n2-1)/ri(n2);
end
cr1, ts=w1*w0, cr=cr1*w0
纯文本文件txt3.txt中的数据格式如下:
1 1 1 4 1 1/2
1 1 2 4 1 1/2
1 1/2 1 5 3 1/2
1/4 1/4 1/5 1 1/3 1/3
1 1 1/3 3 1 1
2 2 2 3 3 1
1 1/4 1/2
4 1 3
2 1/3 1
1 1/4 1/5
4 1 1/2
5 2 1
1 3 1/3
1/3 1 1/7
3 7 1
1 1/3 5
3 1 7
1/5 1/7 1
1 1 7
1 1 7
1/7 1/7 1
1 7 9
1/7 1 1
1/9 1 1
解法二 python文章来源地址https://www.toymoban.com/news/detail-731874.html
import pandas as pd
df = pd.DataFrame({'A': [ 1,1,1,4,1,1/2 ],
'B': [1,1,2,4,1,1/2],
'C': [1,1/2,1,5,3,1/2],
'D': [1/4,1/4,1/5,1,1/3,1/3],
'E': [1,1,1/3,3,1,1],
'F':[2,2,2,3,3,1 ],'})
print(df.corr(method='pearson'))
到了这里,关于五、数学建模之层次分析法的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!