手撕二叉树-Toy模板网

这篇具有很好参考价值的文章主要介绍了手撕二叉树。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

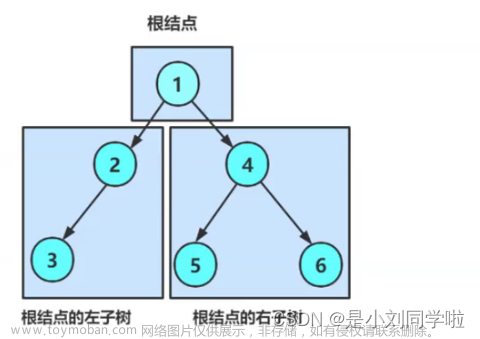
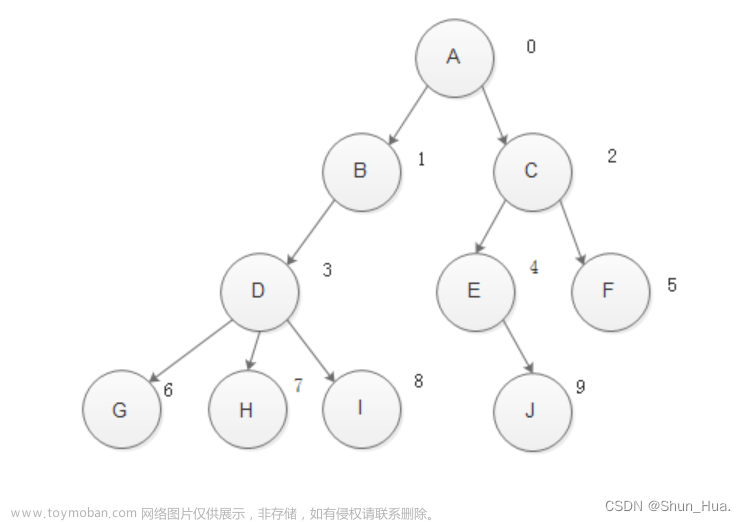
前序遍历构建二叉树

手撕二叉树,数据结构,数据结构,算法

二叉树的销毁

手撕二叉树,数据结构,数据结构,算法

二叉树的结点个数

手撕二叉树,数据结构,数据结构,算法

二叉树叶子节点个数

手撕二叉树,数据结构,数据结构,算法

二叉树第k层节点个数

手撕二叉树,数据结构,数据结构,算法

二叉树查找值为x的节点

手撕二叉树,数据结构,数据结构,算法

二叉树前序遍历

手撕二叉树,数据结构,数据结构,算法

二叉树中序遍历

手撕二叉树,数据结构,数据结构,算法

二叉树后序遍历

手撕二叉树,数据结构,数据结构,算法

二叉树的层序遍历

手撕二叉树,数据结构,数据结构,算法

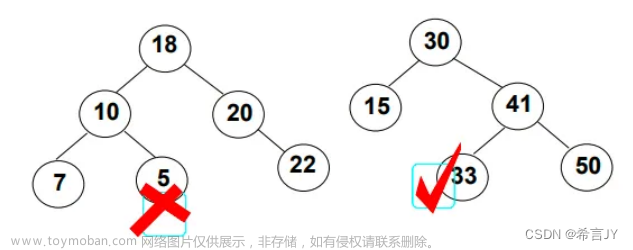
判断二叉树是否是完全二叉树

手撕二叉树,数据结构,数据结构,算法

手撕二叉树,数据结构,数据结构,算法文章来源地址https://www.toymoban.com/news/detail-732446.html

完整代码

test.c

#define _CRT_SECURE_NO_WARNINGS 1

#include <stdio.h>
#include <assert.h>
#include <stdlib.h>

typedef int BTDataType;

typedef struct BinaryTreeNode
{
	struct  BinaryTreeNode* left;
	struct  BinaryTreeNode* right;
	BTDataType val;
}BTNode;

#include "Queue.h"

// 通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
BTNode* BinaryTreeCreate(BTDataType* a, int* pi)
{
	if (a[*pi] == -1)
	{
		++(*pi);
		return NULL;
	}

	BTNode* root = (BTNode*)malloc(sizeof(BTNode));
	root->val = a[*pi];
	++(*pi);

	root->left = BinaryTreeCreate(a, pi);
	root->right = BinaryTreeCreate(a, pi);
	return root;
}

 //二叉树销毁
void BinaryTreeDestory(BTNode** root)
{
	if (*root == NULL)
	{
		return;
	}
	BinaryTreeDestory(&(*root)->left);
	BinaryTreeDestory(&(*root)->right);
	free(*root);
	*root = NULL;
}

// 二叉树节点个数
int BinaryTreeSize(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}

	return BinaryTreeSize(root->left) + BinaryTreeSize(root->right) + 1;
}

// 二叉树叶子节点个数
int BinaryTreeLeafSize(BTNode* root)
{
	if (root == NULL)
	{
		return 0;
	}

	if (root->left == NULL && root->right == NULL)
	{
		return 1;
	}

	return BinaryTreeLeafSize(root->left) + BinaryTreeLeafSize(root->right);
}

// 二叉树第k层节点个数
int BinaryTreeLevelKSize(BTNode* root, int k)
{
	if (root == NULL)
	{
		return 0;
	}

	if (k == 1)
	{
		return 1;
	}

	return BinaryTreeLevelKSize(root->left, k-1) + BinaryTreeLevelKSize(root->right, k-1);
}

// 二叉树前序遍历 
void BinaryTreePrevOrder(BTNode* root)
{
	if (root == NULL)
	{
		return;
	}

	printf("%d ", root->val);
	BinaryTreePrevOrder(root->left);
	BinaryTreePrevOrder(root->right);
}

// 二叉树查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{
	if (root == NULL)
	{
		return NULL;
	}

	if (root->val == x)
	{
		return root;
	}

	BTNode* ret = NULL;
	ret = BinaryTreeFind(root->left, x);
	if (ret)
	{
		return ret;
	}
	ret = BinaryTreeFind(root->right, x);
	if (ret)
	{
		return ret;
	}

	return NULL;
}

// 二叉树中序遍历
void BinaryTreeInOrder(BTNode* root)
{
	if (root == NULL)
	{
		return;
	}

	BinaryTreeInOrder(root->left);
	printf("%d ", root->val);
	BinaryTreeInOrder(root->right);
}

// 二叉树后序遍历
void BinaryTreePostOrder(BTNode* root)
{
	if (root == NULL)
	{
		return;
	}

	BinaryTreePostOrder(root->left);
	BinaryTreePostOrder(root->right);
	printf("%d ", root->val);
}

// 层序遍历
void BinaryTreeLevelOrder(BTNode* root)
{
	Que q;
	QueueInit(&q);

	if (root)
	{
		QueuePush(&q, root);
	}

	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);

		if (front->left)
		{
			QueuePush(&q, front->left);
		}
		if (front->right)
		{
			QueuePush(&q, front->right);
		}

		QueuePop(&q);
		printf("%d ", front->val);
	}
	QueueDestroy(&q);
}

// 判断二叉树是否是完全二叉树
bool BinaryTreeComplete(BTNode* root)
{
	Que q;
	QueueInit(&q);

	if (root)
	{
		QueuePush(&q, root);
	}

	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		if (front == NULL)
		{
			break;
		}
		QueuePush(&q, front->left);
		QueuePush(&q, front->right);
		QueuePop(&q);
	}

	while (!QueueEmpty(&q))
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);

		if (front != NULL)
		{
			QueueDestroy(&q);
			return false;
		}
	}
	QueueDestroy(&q);
	return true;
}

int main()
{
	int a[] = { 1,3,5,-1,-1,2,-1,-1,1,-1,1,-1,-1 };
	int j = 0;
	BTNode* root=BinaryTreeCreate(a, &j);
	bool x = BinaryTreeComplete(root);
	printf("%d", x);
	return 0;
}

Queue.h

#pragma once

#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>

typedef struct BinaryTreeNode* QDataType;
typedef struct QueueNode
{
	struct QueueNode* next;
	QDataType data;
}QNode;

typedef struct Queue
{
	QNode* head;
	QNode* tail;
	int size;
}Que;

void QueueInit(Que* pq);
void QueueDestroy(Que* pq);
void QueuePush(Que* pq, QDataType x);
void QueuePop(Que* pq);
QDataType QueueFront(Que* pq);
QDataType QueueBack(Que* pq);
bool QueueEmpty(Que* pq);
int QueueSize(Que* pq);

Queue.c

#define _CRT_SECURE_NO_WARNINGS 1

#include "Queue.h"

void QueueInit(Que* pq)
{
	assert(pq);

	pq->head = pq->tail = NULL;
	pq->size = 0;
}

void QueueDestroy(Que* pq)
{
	assert(pq);

	QNode* cur = pq->head;
	while (cur)
	{
		QNode* next = cur->next;
		free(cur);
		cur = next;
	}

	pq->head = pq->tail = NULL;
	pq->size = 0;
}

void QueuePush(Que* pq, QDataType x)
{
	assert(pq);

	QNode* newnode = (QNode*)malloc(sizeof(QNode));
	if (newnode == NULL)
	{
		perror("malloc fail");
		exit(-1);
	}

	newnode->data = x;
	newnode->next = NULL;

	if (pq->tail == NULL)
	{
		pq->head = pq->tail = newnode;
	}
	else
	{
		pq->tail->next = newnode;
		pq->tail = newnode;
	}

	pq->size++;
}

void QueuePop(Que* pq)
{
	assert(pq);
	assert(!QueueEmpty(pq));

	if (pq->head->next == NULL)
	{
		free(pq->head);
		pq->head = pq->tail = NULL;
	}
	else
	{
		QNode* next = pq->head->next;
		free(pq->head);
		pq->head = next;
	}

	pq->size--;
}

QDataType QueueFront(Que* pq)
{
	assert(pq);
	assert(!QueueEmpty(pq));

	return pq->head->data;
}

QDataType QueueBack(Que* pq)
{
	assert(pq);
	assert(!QueueEmpty(pq));

	return pq->tail->data;
}

bool QueueEmpty(Que* pq)
{
	assert(pq);

	return pq->head == NULL;
}

int QueueSize(Que* pq)
{
	assert(pq);

	return pq->size;
}

到了这里，关于手撕二叉树的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！