数据结构——八叉树-Toy模板网

这篇具有很好参考价值的文章主要介绍了数据结构——八叉树。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

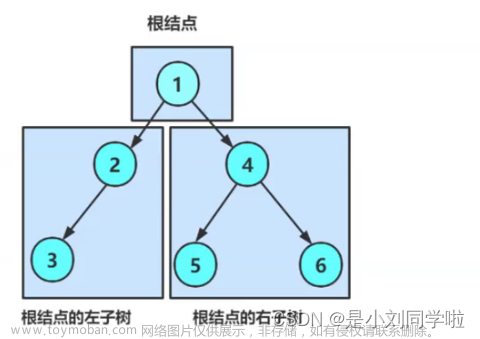
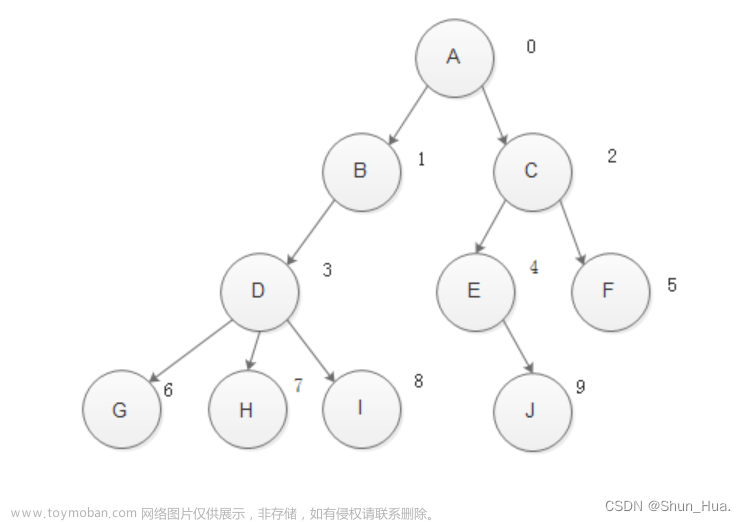
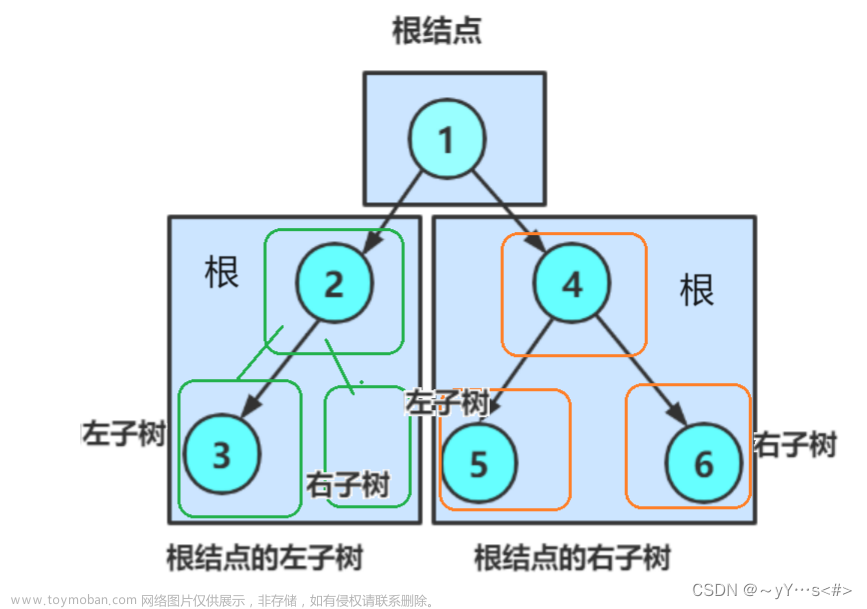
八叉树（Octree）是一种用于表示和管理三维空间的树状数据结构。它将三维空间递归地分割成八个八分体（octant），每个八分体可以继续分割，以实现对三维空间的更精细的划分。八叉树通常用于解决空间搜索和查询问题，例如三维物体碰撞检测、体素化（Voxelization）、地理信息系统等领域。

八叉树,数据结构,数据结构,服务器,数据库文章来源地址https://www.toymoban.com/news/detail-732638.html

#include <iostream>
#include <vector>

// 定义三维点的结构体
struct Point3D {
    float x;
    float y;
    float z;
    Point3D(float _x, float _y, float _z) : x(_x), y(_y), z(_z) {}
};

// 定义八叉树节点
struct OctreeNode {
    Point3D center;
    float size;
    OctreeNode* children[8];

    OctreeNode(Point3D _center, float _size) : center(_center), size(_size) {
        for (int i = 0; i < 8; i++) {
            children[i] = nullptr;
        }
    }
};

class Octree {
private:
    OctreeNode* root;
    float rootSize;

    // 在指定深度下递归插入节点
    OctreeNode* insert(OctreeNode* node, Point3D point, float size) {
        if (node == nullptr) {
            return new OctreeNode(point, size);
        }

        // 确定点位于八分体的哪个子节点
        int index = 0;
        if (point.x >= node->center.x) index |= 1;
        if (point.y >= node->center.y) index |= 2;
        if (point.z >= node->center.z) index |= 4;

        // 递归插入到相应的子节点
        float newSize = node->size / 2.0f;
        node->children[index] = insert(node->children[index], point, newSize);

        return node;
    }

    // 在指定深度下递归搜索节点
    bool search(OctreeNode* node, Point3D point, float size) {
        if (node == nullptr) {
            return false;
        }

        if (node->center.x == point.x && node->center.y == point.y && node->center.z == point.z) {
            return true;
        }

        // 确定点位于八分体的哪个子节点
        int index = 0;
        if (point.x >= node->center.x) index |= 1;
        if (point.y >= node->center.y) index |= 2;
        if (point.z >= node->center.z) index |= 4;

        // 递归搜索相应的子节点
        float newSize = node->size / 2.0f;
        return search(node->children[index], point, newSize);
    }

public:
    Octree(float size) : root(nullptr), rootSize(size) {}

    // 插入一个点
    void insert(Point3D point) {
        root = insert(root, point, rootSize);
    }

    // 搜索一个点是否存在
    bool search(Point3D point) {
        return search(root, point, rootSize);
    }
};

int main() {
    Octree octree(100.0f); // 创建八叉树，定义根节点的大小

    Point3D point1(10.0f, 20.0f, 30.0f);
    Point3D point2(80.0f, 90.0f, 110.0f);

    octree.insert(point1); // 插入点1
    octree.insert(point2); // 插入点2

    Point3D searchPoint(80.0f, 90.0f, 110.0f);
    bool found = octree.search(searchPoint); // 搜索点2
    if (found) {
        std::cout << "Point found in the octree." << std::endl;
    } else {
        std::cout << "Point not found in the octree." << std::endl;
    }

    return 0;
}