1. Toy模板网首页
  2. > Toy博客

C语言实现非递归先序、中序、后序遍历

7月前 作者：呵呵哒(￣▽￣)" 分类：Toy博客 阅读(22) 违法举报

这篇具有很好参考价值的文章主要介绍了C语言实现非递归先序、中序、后序遍历。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

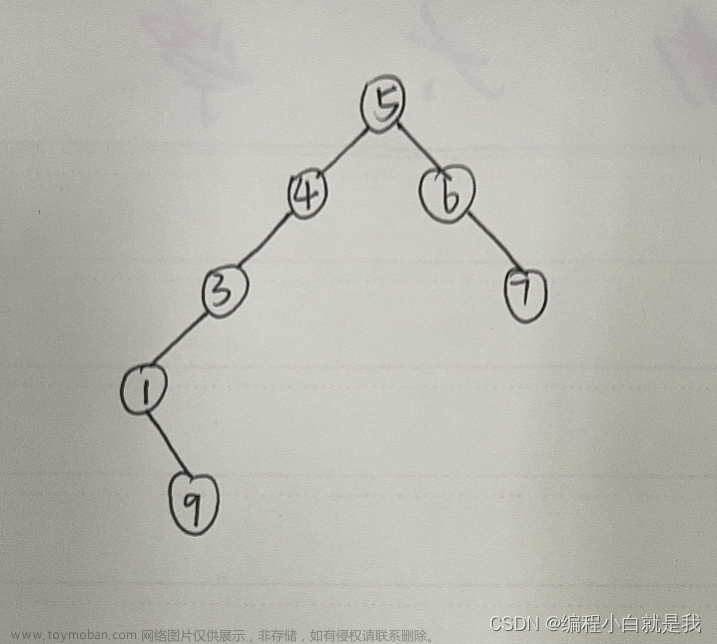
闲来无事，回顾一下以前的学过的数据结构知识，面试也可以用到！！！

中序遍历非递归算法c语言,C++,数据结构,c语言,数据结构,算法

  1、创建一颗二叉树

typedef int ElemType;
typedef struct BiNode {
	ElemType data;
	BiNode* lchild;
	BiNode* rchild;
}BiNode, * BiTree;

//构建二叉树
BiNode* Create(BiNode* bt) {
	static int i = 0;
	char ch;
	//string str = "AB#D##C##";
	//string str = "124##56##7##3##";
	string str = "ABD#G##E##CF###";
	ch = str[i++];
	if (ch == '#')bt = NULL;//建立一棵空树 
	else {
		bt = (BiTree)malloc(sizeof(BiNode)); bt->data = ch;//生成一个结点，数据域为ch
		bt->lchild = Create(bt->lchild);//递归建立左子树
		bt->rchild = Create(bt->rchild);//递归建立右子树
	}
	return bt;
}

2、栈

#define MaxSize 100//定义栈中元素的最大个数
typedef struct {
	BiTree data[MaxSize];//存放栈中元素
	int top;//栈顶指针
}SqStack;
//（1）初始化
void InitStack(SqStack& S) {
	S.top = -1;//初始化栈顶指针
	//S.data[0] = NULL;
}
//（2）判栈空
bool IsEmpty(SqStack& S) {
	if (S.top == -1) {//栈空
		return true;
	}
	else {//不空
		return false;
	}
}
//（3）进栈
bool Push(SqStack& S, BiTree& p) {
	if (S.top == MaxSize - 1) {//栈满，报错
		return false;
	}
	S.data[++S.top] = p;//指针先加1，再加入栈
	return true;
}
//（4）出栈
bool Pop(SqStack& S, BiTree& p) {
	if (S.top == -1) {//栈空，报错
		return false;
	}
	p = S.data[S.top--];//先出栈，指针再减1
	return true;
}
//（5）读栈顶元素
bool GetTop(SqStack& S, BiTree& p) {
	if (S.top == -1) {//栈空，报错
		return false;
	}
	p = S.data[S.top];//先出栈，指针再减1
	return true;
}

3、非递归中序遍历

第一种：非递归中序遍历算法 

void visit(int x) {
	printf("%c ", x);
}

void InOrder(BiTree T) {
	SqStack S;
	InitStack(S);
	BiNode* p, * r;
	p = T;
	r = NULL;
	while (p || !IsEmpty(S)) {
		if (p) {//一路向左
			Push(S, p);
			p = p->lchild;
		}
		else {
			Pop(S, p);
			visit(p->data);
			p = p->rchild;//判断右孩子
		}
	}
}

中序遍历非递归算法c语言,C++,数据结构,c语言,数据结构,算法

第二种：非递归中序遍历算法

伪代码和算法详解：

中序遍历非递归算法c语言,C++,数据结构,c语言,数据结构,算法

void visit(int x) {
	printf("%c ", x);
}
void InOrder(BiTree T) {
	SqStack S;
	InitStack(S);
	BiNode* p, * r;
	p = T;
	r = NULL;
	while (p || !IsEmpty(S)) {
		while (p) {//一路向左
			Push(S, p);
			p = p->lchild;
		}
		if(!IsEmpty(S)) {
			Pop(S, p);
			visit(p->data);
			p = p->rchild;//判断右孩子
		}
	}//while
}

4.非递归中序遍历完整代码

#include<stdio.h>
#include<stdlib.h>
#include<iostream>
using namespace std;

typedef int ElemType;
typedef struct BiNode {
	ElemType data;
	BiNode* lchild;
	BiNode* rchild;
}BiNode, * BiTree;

//构建二叉树
BiNode* Create(BiNode* bt) {
	static int i = 0;
	char ch;
	//string str = "AB#D##C##";
	//string str = "124##56##7##3##";
	string str = "ABD#G##E##CF###";
	ch = str[i++];
	if (ch == '#')bt = NULL;//建立一棵空树 
	else {
		bt = (BiTree)malloc(sizeof(BiNode)); bt->data = ch;//生成一个结点，数据域为ch
		bt->lchild = Create(bt->lchild);//递归建立左子树
		bt->rchild = Create(bt->rchild);//递归建立右子树
	}
	return bt;
}


#define MaxSize 100//定义栈中元素的最大个数
typedef struct {
	BiTree data[MaxSize];//存放栈中元素
	int top;//栈顶指针
}SqStack;
//（1）初始化
void InitStack(SqStack& S) {
	S.top = -1;//初始化栈顶指针
	//S.data[0] = NULL;
}
//（2）判栈空
bool IsEmpty(SqStack& S) {
	if (S.top == -1) {//栈空
		return true;
	}
	else {//不空
		return false;
	}
}
//（3）进栈
bool Push(SqStack& S, BiTree& p) {
	if (S.top == MaxSize - 1) {//栈满，报错
		return false;
	}
	S.data[++S.top] = p;//指针先加1，再加入栈
	return true;
}
//（4）出栈
bool Pop(SqStack& S, BiTree& p) {
	if (S.top == -1) {//栈空，报错
		return false;
	}
	p = S.data[S.top--];//先出栈，指针再减1
	return true;
}
//（5）读栈顶元素
bool GetTop(SqStack& S, BiTree& p) {
	if (S.top == -1) {//栈空，报错
		return false;
	}
	p = S.data[S.top];//先出栈，指针再减1
	return true;
}
void visit(int x) {
	printf("%c ", x);
}

void InOrder(BiTree T) {
	SqStack S;
	InitStack(S);
	BiNode* p, * r;
	p = T;
	r = NULL;
	while (p || !IsEmpty(S)) {
		if (p) {//一路向左
			Push(S, p);
			p = p->lchild;
		}
		else {
			Pop(S, p);
			visit(p->data);
			p = p->rchild;//判断右孩子
		}
		
	}//while
}

void DInOrder(BiTree T) {
	if (T != NULL) {
		DInOrder(T->lchild);//后序遍历左子树
		visit(T->data);//访问根节点的数据域
		DInOrder(T->rchild);//后序遍历右子树
	}
}
int main() {
	//创建一棵二叉树
	BiTree T = (BiTree)malloc(sizeof(BiNode));//创建一颗二叉树
	T = Create(T);
	//递归先序遍历
	printf("递归中序遍历 \n");
	DInOrder(T);

	printf("\n非递归中序遍历 \n");
	//非递归后序遍历
	InOrder(T);
}

演示效果：

中序遍历非递归算法c语言,C++,数据结构,c语言,数据结构,算法中序遍历非递归算法c语言,C++,数据结构,c语言,数据结构,算法

 中序遍历非递归算法c语言,C++,数据结构,c语言,数据结构,算法中序遍历非递归算法c语言,C++,数据结构,c语言,数据结构,算法

 5.非递归先序遍历

第一种：非递归先序遍历

void visit(int x) {
	printf("%c ", x);
}

void PreOrder(BiTree T) {
	SqStack S;
	InitStack(S);
	BiNode* p, * r;
	p = T;
	r = NULL;
	while (p || !IsEmpty(S)) {
		if (p) {//一路向左
			visit(p->data);//访问该结点
			Push(S, p);
			p = p->lchild;
		}
		else {
			//GetTop(S, p);
			Pop(S, p);//栈顶元素出栈
			p = p->rchild;//向右寻找
		}//else
	}//while
}

中序遍历非递归算法c语言,C++,数据结构,c语言,数据结构,算法

第二种：非递归先序遍历

中序遍历非递归算法c语言,C++,数据结构,c语言,数据结构,算法

void visit(int x) {
	printf("%c ", x);
}
void PreOrder(BiTree T) {
	SqStack S;
	InitStack(S);
	BiNode* p, * r;
	p = T;
	r = NULL;
	while (p || !IsEmpty(S)) {
		while (p) {//一路向左
			visit(p->data);//访问该结点
			Push(S, p);
			p = p->lchild;
		}
		if(!IsEmpty(S)) {
			Pop(S, p);//栈顶元素出栈
			p = p->rchild;//向右寻找
		}
	}
}

演示效果： 

中序遍历非递归算法c语言,C++,数据结构,c语言,数据结构,算法中序遍历非递归算法c语言,C++,数据结构,c语言,数据结构,算法

中序遍历非递归算法c语言,C++,数据结构,c语言,数据结构,算法中序遍历非递归算法c语言,C++,数据结构,c语言,数据结构,算法

  6.非递归先序遍历完整代码

#include<stdio.h>
#include<stdlib.h>
#include<iostream>
using namespace std;

typedef int ElemType;
typedef struct BiNode {
	ElemType data;
	BiNode* lchild;
	BiNode* rchild;
}BiNode, * BiTree;

//构建二叉树
BiNode* Create(BiNode* bt) {
	static int i = 0;
	char ch;
	//string str = "AB#D##C##";
	//string str = "124##56##7##3##";
	string str = "ABD#G##E##CF###";
	ch = str[i++];
	if (ch == '#')bt = NULL;//建立一棵空树 
	else {
		bt = (BiTree)malloc(sizeof(BiNode)); bt->data = ch;//生成一个结点，数据域为ch
		bt->lchild = Create(bt->lchild);//递归建立左子树
		bt->rchild = Create(bt->rchild);//递归建立右子树
	}
	return bt;
}


#define MaxSize 100//定义栈中元素的最大个数
typedef struct {
	BiTree data[MaxSize];//存放栈中元素
	int top;//栈顶指针
}SqStack;
//（1）初始化
void InitStack(SqStack& S) {
	S.top = -1;//初始化栈顶指针
	//S.data[0] = NULL;
}
//（2）判栈空
bool IsEmpty(SqStack& S) {
	if (S.top == -1) {//栈空
		return true;
	}
	else {//不空
		return false;
	}
}
//（3）进栈
bool Push(SqStack& S, BiTree& p) {
	if (S.top == MaxSize - 1) {//栈满，报错
		return false;
	}
	S.data[++S.top] = p;//指针先加1，再加入栈
	return true;
}
//（4）出栈
bool Pop(SqStack& S, BiTree& p) {
	if (S.top == -1) {//栈空，报错
		return false;
	}
	p = S.data[S.top--];//先出栈，指针再减1
	return true;
}
//（5）读栈顶元素
bool GetTop(SqStack& S, BiTree& p) {
	if (S.top == -1) {//栈空，报错
		return false;
	}
	p = S.data[S.top];//先出栈，指针再减1
	return true;
}
void visit(int x) {
	printf("%c ", x);
}

void PreOrder(BiTree T) {
	SqStack S;
	InitStack(S);
	BiNode* p, * r;
	p = T;
	r = NULL;
	while (p || !IsEmpty(S)) {
		if (p) {//一路向左
			visit(p->data);//访问该结点
			Push(S, p);
			p = p->lchild;
		}
		else {
			//GetTop(S, p);
			Pop(S, p);//栈顶元素出栈
			p = p->rchild;//向右寻找
		}//else
	}//while
}

void DPreOrder(BiTree T) {
	if (T != NULL) {
		visit(T->data);//访问根节点的数据域
		DPreOrder(T->lchild);//后序遍历左子树
		DPreOrder(T->rchild);//后序遍历右子树
	}
}
int main() {
	//创建一棵二叉树
	BiTree T = (BiTree)malloc(sizeof(BiNode));//创建一颗二叉树
	T = Create(T);
	//递归先序遍历
	printf("递归先序遍历 \n");
	DPreOrder(T);

	printf("\n非递归先序遍历 \n");
	//非递归后序遍历
	PreOrder(T);
}

  7.非递归后序遍历

void visit(int x) {
	printf("%c ", x);
}

void PostOrder(BiTree T) {
	SqStack S;
	InitStack(S);
	BiNode* p,*r;
	p = T;
	r = NULL;
	while (p || !IsEmpty(S)) {
		if (p) {//走到最左边
			Push(S, p);
			p = p->lchild;
		}
		else {//向右
			GetTop(S, p);//向右
			if (p->rchild && p->rchild != r) {//如果右子树存在，且未被访问过
				p = p->rchild;//转向右
				Push(S, p);//压入栈
				p = p->lchild;//再走到最左
			}
			else {
				Pop(S, p);//将结点弹出
				visit(p->data);//访问该结点
				r = p;//记录最近访问过的结点
				p = NULL;//结点访问完后，重置p指针
			}
		}//else
	}//while
}

中序遍历非递归算法c语言,C++,数据结构,c语言,数据结构,算法

演示效果： 

中序遍历非递归算法c语言,C++,数据结构,c语言,数据结构,算法中序遍历非递归算法c语言,C++,数据结构,c语言,数据结构,算法

中序遍历非递归算法c语言,C++,数据结构,c语言,数据结构,算法中序遍历非递归算法c语言,C++,数据结构,c语言,数据结构,算法

  8.非递归后序遍历完整代码

#include<stdio.h>
#include<stdlib.h>
#include<iostream>
using namespace std;

typedef int ElemType;
typedef struct BiNode {
	ElemType data;
	BiNode* lchild;
	BiNode* rchild;
}BiNode, *BiTree;

//构建二叉树
BiNode* Create(BiNode* bt) {
	static int i = 0;
	char ch;
	//string str = "AB#D##C##";
	//string str = "124##56##7##3##";
	string str = "ABD#G##E##CF###";
	ch = str[i++];
	if (ch == '#')bt = NULL;//建立一棵空树 
	else {
		bt = (BiTree)malloc(sizeof(BiNode)); bt->data = ch;//生成一个结点，数据域为ch
		bt->lchild = Create(bt->lchild);//递归建立左子树
		bt->rchild = Create(bt->rchild);//递归建立右子树
	}
	return bt;
}


#define MaxSize 100//定义栈中元素的最大个数
typedef struct {
	BiTree data[MaxSize];//存放栈中元素
	int top;//栈顶指针
}SqStack;
//（1）初始化
void InitStack(SqStack &S) {
	S.top = -1;//初始化栈顶指针
	//S.data[0] = NULL;
}
//（2）判栈空
bool IsEmpty(SqStack& S) {
	if (S.top == -1) {//栈空
		return true;
	}
	else {//不空
		return false;
	}
}
//（3）进栈
bool Push(SqStack& S, BiTree &p) {
	if (S.top == MaxSize-1) {//栈满，报错
		return false;
	}
	S.data[++S.top] = p;//指针先加1，再加入栈
	return true;
}
//（4）出栈
bool Pop(SqStack& S, BiTree& p) {
	if (S.top == - 1) {//栈空，报错
		return false;
	}
	p = S.data[S.top--];//先出栈，指针再减1
	return true;
}
//（5）读栈顶元素
bool GetTop(SqStack& S, BiTree& p) {
	if (S.top == -1) {//栈空，报错
		return false;
	}
	p = S.data[S.top];//先出栈，指针再减1
	return true;
}
void visit(int x) {
	printf("%c ", x);
}

void PostOrder(BiTree T) {
	SqStack S;
	InitStack(S);
	BiNode* p,*r;
	p = T;
	r = NULL;
	while (p || !IsEmpty(S)) {
		if (p) {//走到最左边
			Push(S, p);
			p = p->lchild;
		}
		else {//向右
			GetTop(S, p);//向右
			if (p->rchild && p->rchild != r) {//如果右子树存在，且未被访问过
				p = p->rchild;//转向右
				Push(S, p);//压入栈
				p = p->lchild;//再走到最左
			}
			else {
				Pop(S, p);//将结点弹出
				visit(p->data);//访问该结点
				r = p;//记录最近访问过的结点
				p = NULL;//结点访问完后，重置p指针
			}
		}//else
	}//while
}

void DPostOrder(BiTree T) {
	if (T != NULL) {
		DPostOrder(T->lchild);//后序遍历左子树
		DPostOrder(T->rchild);//后序遍历右子树
		//visit(T->data);//访问根节点的数据域
		//cout << "heheda" << endl;
		visit(T->data);//访问根节点的数据域
	}
}
int main() {
	//创建一棵二叉树
	BiTree T = (BiTree)malloc(sizeof(BiNode));//创建一颗二叉树
	T = Create(T);
	//递归后序遍历
	printf("递归后序遍历 \n");
	DPostOrder(T);
	printf("\n非递归后序遍历 \n");
	//非递归后序遍历
	PostOrder(T);
}

过程推演是小编的想法，如有不对的地方，欢迎指正，我将继续制作出更加有质量的博客内容，希望个位小伙伴能够点个赞，这是对我的付出的肯定，谢谢您们！！！ 

我的近期文章，C++版本：

C++ 图解二叉树非递归中序 + 实战力扣题-CSDN博客https://blog.csdn.net/weixin_41987016/article/details/134287291?csdn_share_tail=%7B%22type%22%3A%22blog%22%2C%22rType%22%3A%22article%22%2C%22rId%22%3A%22134287291%22%2C%22source%22%3A%22weixin_41987016%22%7D
C++ 图解二叉树非递归后序 + 实战力扣题-CSDN博客https://blog.csdn.net/weixin_41987016/article/details/134287728?csdn_share_tail=%7B%22type%22%3A%22blog%22%2C%22rType%22%3A%22article%22%2C%22rId%22%3A%22134287728%22%2C%22source%22%3A%22weixin_41987016%22%7D

 文章来源地址https://www.toymoban.com/news/detail-732748.html

到了这里，关于C语言实现非递归先序、中序、后序遍历的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处： 如若内容造成侵权/违法违规/事实不符，请点击违法举报进行投诉反馈，一经查实，立即删除！

分享到：
领支付宝红包 赞助服务器费用

相关文章

  • C语言完整代码实现：二叉树的先序遍历、中序遍历、后序遍历

    C语言完整代码实现：二叉树的先序遍历、中序遍历、后序遍历

    一、先序遍历原理        先序遍历就是： 根、左、右 ，也就是先遍历根结点再遍历左结点最后再遍历右结点，注意：如果遍历到的结点不是叶子结点的话需要对该结点进行拆分，比如这棵二叉树： 先遍历 A ，然后是 B ，然后再是 C ，但是由于B并不是叶子结点，他本身又是

    2024年02月07日
    浏览(37)
  • 【数据结构】二叉树的创建和遍历（先序、中序、后序）

    【数据结构】二叉树的创建和遍历（先序、中序、后序）

    最近一段时间学习了数据结构中二叉树的基本操作，包括二叉树的结构、二叉树的创建、递归先序中序后序遍历、非递归遍历等，想着把二叉树的相关知识和自己的见解放到网上来让网友看看是否正确，想和网友一起共同交流。 先了解一下二叉树的三个基本性质： 性质1：在

    2024年02月04日
    浏览(35)
  • 数据结构——二叉树先序、中序、后序三种遍历

    数据结构——二叉树先序、中序、后序三种遍历

    先序遍历可以想象为，一个小人从一棵二叉树根节点为起点，沿着二叉树外沿，逆时针走一圈回到根节点，路上遇到的元素顺序，就是先序遍历的结果 先序遍历结果为：A B D H I E J C F K G 动画演示： 记住小人沿着外围跑一圈（直到跑回根节点），多看几次动图便能理解    

    2024年02月11日
    浏览(42)
  • 7-1 根据后序和中序遍历输出先序遍历 (PTA-数据结构)

    7-1 根据后序和中序遍历输出先序遍历 (PTA-数据结构)

    本题要求根据给定的一棵二叉树的后序遍历和中序遍历结果，输出该树的先序遍历结果。 输入格式: 第一行给出正整数N(≤30)，是树中结点的个数。随后两行，每行给出N个整数，分别对应后序遍历和中序遍历结果，数字间以空格分隔。题目保证输入正确对应一棵二叉树。 输出

    2024年02月03日
    浏览(31)
  • 【数据结构|二叉树遍历】递归与非递归实现前序遍历、中序遍历、后序遍历

    【数据结构|二叉树遍历】递归与非递归实现前序遍历、中序遍历、后序遍历

    递归与非递归实现二叉树的前序遍历、中序遍历、后序遍历。 二叉树图 定义 前序遍历（Preorder Traversal）： 前序遍历的顺序是先访问根节点，然后按照先左后右的顺序访问子节点。对于上面的二叉树，前序遍历的结果是：4 - 2 - 1 - 3 - 6 - 5 - 7。 中序遍历（Inorder Traversal）： 中

    2024年02月14日
    浏览(34)
  • 十三、数据结构——二叉树的遍历（先序、中序和后序）详细思路和代码

    十三、数据结构——二叉树的遍历（先序、中序和后序）详细思路和代码

    在数据结构中，二叉树是一种常用且重要的数据结构。二叉树的遍历是指按照一定顺序访问二叉树的所有节点，常见的遍历方式有前序遍历、中序遍历和后序遍历。本文将详细介绍这三种遍历算法，并介绍最优二叉树。 首先，我们先来了解一下二叉树的基本定义。二叉树是每

    2024年02月15日
    浏览(30)
  • 【数据结构】16 二叉树的定义，性质，存储结构（以及先序、后序、中序遍历）

    【数据结构】16 二叉树的定义，性质，存储结构（以及先序、后序、中序遍历）

    一个二叉树是一个有穷的结点集合。 它是由根节点和称为其左子树和右子树的两个不相交的二叉树组成的。 二叉树可具有以下5种形态。 一个二叉树第i层的最大结点数为 2 i − 1 2^{i-1} 2 i − 1 , i ≥ 1 i geq 1 i ≥ 1 每层最大结点可以对应完美二叉树（满二叉树），其所有分支结

    2024年02月20日
    浏览(35)
  • 二叉树的先序、中序、后序遍历C++

    二叉树的先序、中序、后序遍历C++

    二叉树的节点结构如下所示 如下所示是一个二叉树，其中的每一个节点都是由上述TreeNode节点的一个具体对象。                                 图1 先遍历根（父）节点 、再遍历左节点、最后遍历右节点。 注意：这里说的遍历并不是行走。毕竟我们能够先取到的指针只

    2024年02月15日
    浏览(25)
  • 根据二叉树的先序、中序、后序遍历构建二叉树-图文详解

    根据二叉树的先序、中序、后序遍历构建二叉树-图文详解

    引言：根据一颗二叉树，可以得出他的先序、中序、后序三种遍历方式，那么如果我们知道了他的前序、中序、后序遍历，如何绘制出这颗二叉树呢？ 特性A，对于前序遍历，第⼀个肯定是根节点； 特性B，对于后序遍历，最后⼀个肯定是根节点； 特性C，利⽤前序或后序遍历

    2024年02月06日
    浏览(31)

  • 算法刷题Day14 二叉树的前序、中序、后序遍历（递归、迭代、统一迭代方法）

    二叉树的定义 递归 迭代 普通的遍历（包括前序，中序和后续）迭代方法都需要借助到栈 统一迭代 统一迭代使用标记法，在栈中要处理的结点压入空指针 递归 迭代 中序遍历的迭代方法稍微特殊一点 中序遍历是左中右，先访问的是二叉树顶部的节点，然后一层一层向下访问

    2024年02月15日
    浏览(37)

觉得文章有用就打赏一下文章作者

支付宝扫一扫打赏

博客赞助

微信扫一扫打赏

请作者喝杯咖啡吧~博客赞助

支付宝扫一扫领取红包，优惠每天领

二维码1

领取红包

二维码2

领红包