函数递归详解-Toy模板网

这篇具有很好参考价值的文章主要介绍了函数递归详解。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

前言：

函数递归是一种算法，递归是通过将问题分解为更小的子问题来解决问题的办法，递归的优点如下：

简洁性：递归可以用较少的代码实现复杂的功能

灵活性：递归可以应对未知深度的数据结构，因为它不需要提前知道要处理的嵌套层级

什么是递归？

递归：程序调用自身的编程技巧称为递归；

从调用自身的层面：函数递归就是自己调用自己

从编程技巧层面：一种方法（它通常将一个大型复杂问题层层转化为一个与原问题相似的规模较小的问题来求解，简化程序的代码量），这种方法的主要思想为：将大事化小

史上最简单的递归：

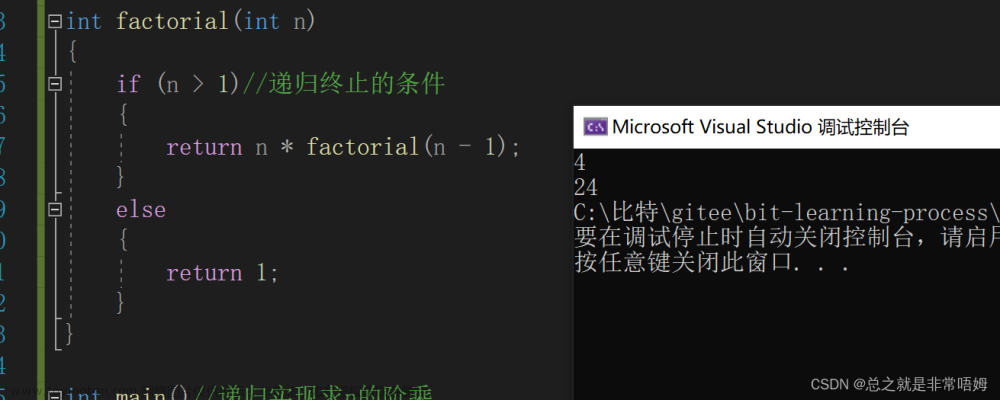
int main()
{
	printf("hehe\n");

	main();

	return 0;
}

main()函数内部调用了main()函数，产生的现象为程序死递归，导致栈溢出（stack overflow）；

递归的两个必要条件

存在限制条件，当满足这个限制条件的时候，递归便不再继续；

每次递归调用之后越来越接近这个限制条件；

递归的细节说明

每一级递归都有自己的参数，参数形式可能相同，但是其值不同

函数调用之前，操作系统会为其分配函数栈帧，从而保留函数调用时当前函数的参数；

每一次函数调用结束都要返回值，当递归执行结束后，控制权转回到上一级函数

当递归的最后一层执行结束，系统释放最后一次递归调用所开辟的空间，同时返回到上一级函数调用，接着向下执行程序，当上一级递归结束，系统继续释放该级调用的函数栈帧，按此循环，直至系统回收主函数所开辟的函数栈帧为止；

函数中递归语句之前的代码，按被调函数的顺序执行，递归之后的代码，与被调函数相反的顺序执行

递归示例

示例1：

接受一个整型值（无符号），按照顺序打印它的每一位

输入：1234 输出：1 2 3 4

思路：

假设定义print()函数，其功能为按照顺序打印每一位

print(1234)即打印1 2 3 4

print(123) 4 按照顺序打印1 2 3，最后打印4；

print(12) 3 按照顺序打印1 2 ，最后打印3；

printf(1) 2 打印1，最后打印2；

当位数只有一位时，不需要进行拆分，直接打印；

//只需要打印，不需要返回值
void print(unsigned int x)
{
	if (x > 9)
	{
		print(x / 10);//剥离n位数的前n-1位
	}
	printf("%d ", x % 10);//打印最后一位
}
int main()
{
	unsigned int num = 0;
	scanf("%d", &num);
	print(num);
	return 0;
}

运行结果：

函数递归详解,算法

画图分析：程序执行过程如箭头所示

函数递归详解,算法

示例2:

求字符串长度

int my_strlen(char* s)
{
	int count = 0;
	while (*s != '\0')
	{
		count++;
		s++;
	}
	return count;
}
int main()
{
	char arr[] = "abc";
	int len = my_strlen(arr);
	printf("%d\n", len);
	return 0;
}

编写函数不允许创建临时变量，求字符串长度

思路：

假设my_strlen()函数可以求字符串长度,参数为字符指针

传参时需要传址，对字符地址进行解引用操作，如果第一个字符就是'\0',长度为0

如果第一个字符不是'\0',长度为1+my_strlen()函数；

例如：

my_strlen("abc")

1+my_strlen("bc")

1+1+my_strlen("c")

1+1+1+my_strlen("")

int my_strlen(char* s)
{

	if (*s == '\0')
		return 0;
	else
		return 1 + my_strlen(s + 1);
}
int main()
{
	char arr[] = "abc";
	int len = my_strlen(arr);
	printf("%d\n", len);
	return 0;
}

示例3：

求第n个斐波那契数

思路：

斐波那契数列：1 1   2   3    5    8   13   21   34    55 ......

斐波那契数的特点前两个数的和等于第三个数

公式：

     当n<=2时， Fib(n)= 1

     当n>2时，     Fib(n)= Fib(n-1)+Fib(n-2)

//递归解法
int Fib(int n)
{
	if (n <= 2)
		return 1;
	else
		return Fib(n - 1) + Fib(n - 2);
}

int main()
{
	int n = 0;
	scanf("%d", &n);
	int ret = Fib(n);
	printf("%d\n", ret);
	return 0;
}

递归的方式求解斐波那契数存在大量重复的计算，导致性能下降，效率低下，解决方案：

采用非递归方式求解

思路：

利用斐波那契数的特点，前两个斐波那契数不用计算

a=1 b=1 c=a+b=2

a=b=1 b=c=2 c=a+b=1+2=3

a=b=2 b=c=3 c=a+b=5

......

//迭代解法
//前两个斐波那契数不用计算，计算第n个斐波那契数即程序执行n-2次
int Fib(int n)
{
	int a = 1;
	int b = 1;
	int c = 1;

	while (n >= 3)
	{
		c = a + b;
		a = b;
		b = c;

		n--;
	}
	return c;
}
int main()
{
	int n = 0;
	scanf("%d", &n);
	int ret = Fib(n);
	printf("%d\n", ret);
	return 0;
}

文章来源地址https://www.toymoban.com/news/detail-733624.html

到了这里，关于函数递归详解的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！