力扣在线OJ——栈和队列-Toy模板网

这篇具有很好参考价值的文章主要介绍了力扣在线OJ——栈和队列。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

🍁一、用两个队列实现栈

🌕（一）、题目（力扣链接：用队列实现栈）

🌕（二）、注意

🌕（三）、解答

⭐️1.注意事项

⭐️2.第一个接口——匿名结构体

⭐️3.第二个接口——MyStack* myStackCreate()

⭐️4.第三个接口——void myStackPush(MyStack* obj, int x)

⭐️5.第四个接口——int myStackPop(MyStack* obj)

⭐️6.第五个接口——int myStackTop(MyStack* obj)

⭐️7.第六个接口——bool myStackEmpty(MyStack* obj)

⭐️8.第七个接口——void myStackFree(MyStack* obj)

🌕（四）、第一题源代码

⭐️1.代码：

⭐️2.运行结果：

🍁二、用栈实现队列

🌕（一）、题目（力扣链接：用栈实现队列）

🌕（二）、思路

🌕（三）、解答

⭐️1.第一个接口——typedef struct

⭐️2.第二个接口——MyQueue* myQueueCreate()

⭐️3.第三个接口——void myQueuePush(MyQueue* obj, int x)

⭐️4.第四个接口——int myQueuePop(MyQueue* obj)

⭐️5.第五个接口——int myQueuePeek(MyQueue* obj)

⭐️6.第六个接口——bool myQueueEmpty(MyQueue* obj)

⭐️7.第七个接口——void myQueueFree(MyQueue* obj)

🌕（四）、第二题源代码

🍁一、用两个队列实现栈

🌕（一）、题目（力扣链接：用队列实现栈）

🌕（二）、注意

与以前不同的是，这次的OJ的练习给了几个函数接口，这几个函数接口就是栈的操作的接口，我们需要用队列来实现，如下：

这需要我们根据函数名来猜测一下每个函数的作用是什么，分析清楚了才能去考虑如何写代码，这大大增加了难度。

🌕（三）、解答

⭐️1.注意事项

（1）.这道题的意思就是，这里又两个队列，并且只提供了队列操作的几个接口，如下：

然后叫我们实现出一个栈；

（2）.首先我们没有队列，所以可以将上一次我们实现的队列复制粘贴过来，因为C语言库里面没有，所以我们要自己实现，等以后我们学习C++，就可以直接使用C++的库里面的各种东西，比如栈和队列就可以直接使用；

⭐️2.第一个接口——匿名结构体

这是一个匿名结构体，感兴趣的小伙伴可以去了解一下，我们是可以更改里面的内容的，我们需要两个队列，所以把里面的内容改为两个队列；

这样后续，我们可以通过MyStack栈来操作两个队列，即用两个队列实现栈。

⭐️3.第二个接口——MyStack* myStackCreate()

①：看函数名的意思就是“我的栈的初始化”；

②:操作很简单，首先先创建一个MyStack栈的指针，然后为其动态分配空间；

然后在使用我们自己的队列接口Queueinit，对栈的成员Que1和Que2进行初始化：
//栈的初始化
MyStack* myStackCreate() {
MyStack *pst=(MyStack*)malloc(sizeof(MyStack));
Queueinit(&pst->q1);
Queueinit(&pst->q2);
return pst;
}

⭐️4.第三个接口——void myStackPush(MyStack* obj, int x)

①：很显然就是“入栈操作”；

②：入栈很简单，我们只需要将入栈的元素入到不为空的队列中即可；

这样就会呈现出一个队列为空，一个队列不为空的局面，方便我们后出栈的思路：
//入栈
void myStackPush(MyStack* obj, int x) {
//根据思路分析，哪个队列不为空，就入队哪个队列
if(!QueueEmpty(&obj->q1))
{
    QueuePush(&obj->q1,x);
}
else
{
    QueuePush(&obj->q2,x);
}
}

⭐️5.第四个接口——int myStackPop(MyStack* obj)

①：按函数名就是“出栈操作”的意思；

②：根据栈和队列的结构：

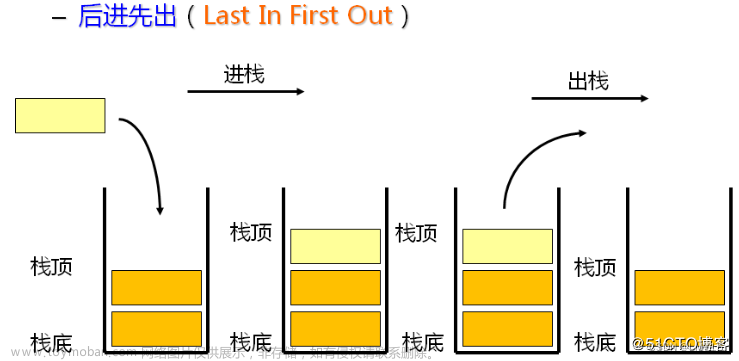
栈为后进先出，队列为先进先出；

所以想要出栈，即为出队队列的队尾元素；

这里又有两个队列，所以可以想到一个思路：

①：首先将不为空的队列的前size-1个元素导入空队列中：

②：此时之前不为空的队列中还剩下一个元素，而此元素即为我们要出栈的元素：

③：完成一轮后，之前不为空的队列就变为空队列，之前的空队列就变为不为空队列了，之后循环操作即可：
//出栈
int myStackPop(MyStack* obj) {
	//根据思路分析，将不为空的队列一的前Size-1个元素导入空队列二；
	//再将不为空的队列一剩余的一个元素出队返回，即为出栈操作；

	//首先我们不知道哪个队列为空，所以我们可以使用“假设法”找出空队列
	Que* empty = &obj->q1;
	Que* noempty = &obj->q2;
	if (!QueueEmpty(&obj->q1))
	{
		empty = &obj->q2;
		noempty = &obj->q1;
	}

	//然后将不为空的队列的前size-1个元素导入空队列
	while (QueueSize(noempty) > 1)
	{
		//取不为空队列的队头，导入空队列
		QueuePush(empty, QueueFront(noempty));
		//不为空队列出队，导入下一个元素
		QueuePop(noempty);
	}

	//到这里，不为空的队列只剩下一个元素，即我们需要出栈的元素；

	//保存该元素
	int top = QueueFront(noempty);
	//出队
	QueuePop(noempty);
	//返回
	return top;
}

⭐️6.第五个接口——int myStackTop(MyStack* obj)

①：看函数名意为“返回栈顶元素”；

②：思路：根据栈和队列的使用规则或者上述出栈操作的思路，我们应该清楚，栈的栈顶即为队列的队尾元素；

③：步骤：所以我们只需要找到不为空的队列然后返回其队尾元素即可；
//返回栈顶元素
int myStackTop(MyStack* obj) {
	//因为栈为后进先出，队列为先进先出，所以要返回栈顶元素，即返回不为空队列的队尾元素
	if (!QueueEmpty(&obj->q1))
	{
		return QueueBack(&obj->q1);
	}
	else
	{
		return QueueBack(&obj->q2);
	}
}

⭐️7.第六个接口——bool myStackEmpty(MyStack* obj)

①：看函数名意为“判断栈空”

②:只需要看两个队列是否同时为空，若两个队列同时为空，则栈空；
//栈的判空
bool myStackEmpty(MyStack* obj) {
	//两队列为空，即栈为空，所以直接用逻辑值判断
	return QueueEmpty(&obj->q1) && QueueEmpty(&obj->q2);
}

⭐️8.第七个接口——void myStackFree(MyStack* obj)

①：函数名意为“栈的销毁”；

②：我们要注意，除了要释放动态开辟的MyStack空间，之前还要将两个队列给释放掉；
//栈的销毁
void myStackFree(MyStack* obj) {
	QueueDestroy(&obj->q1);
	QueueDestroy(&obj->q2);
	free(obj);
}

🌕（四）、第一题源代码

⭐️1.代码：

#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>
#include<assert.h>


typedef int QDatatype;
typedef struct QueueNode
{
	struct QueueNode* next;
	QDatatype data;
}QNode;

typedef struct Queue
{
	QNode* head;//头指针，指向首结点
	QNode* tail;//尾指针，指向为结点
	int size;//记录队列长度
}Que;

//初始化
void Queueinit(Que* ps);

//销毁
void QueueDestroy(Que* ps);

//入队
void QueuePush(Que* ps, QDatatype x);

//出队
void QueuePop(Que* ps);

//取队头
QDatatype QueueFront(Que* ps);

//取队尾
QDatatype QueueBack(Que* ps);

//判空
bool QueueEmpty(Que* ps);

//获取队列元素个数
int QueueSize(Que* ps);


//初始化
void Queueinit(Que* ps)
{
	assert(ps);
	ps->head = ps->tail = NULL;
	ps->size = 0;
}

//销毁
void QueueDestroy(Que* ps)
{
	assert(ps);
	QNode* cur = ps->head;
	//先保存下一个结点，在释放当前结点，在重定位
	while (cur)
	{
		QNode* Qnext = cur->next;
		free(cur);
		cur = Qnext;
	}
	ps->head = ps->tail = NULL;
	ps->size = 0;
}

//入队
void QueuePush(Que* ps, QDatatype x)
{
	assert(ps);
	//创建一个新结点
	QNode* newnode = (QNode*)malloc(sizeof(QNode));
	if (newnode == NULL)
	{
		perror("malloc");
		return;
	}
	//因为是在尾结点入队，所以入队之后结点next域要置空
	newnode->data = x;
	newnode->next = NULL;
	//第一次插入是结构体指针之间的赋值,之后才是结构体成员的赋值，所以要分情况
	//记住tail指针始终指向尾结点，所以入队之后要对tail指针重定位
	if (ps->tail == NULL)
	{
		ps->head = ps->tail = newnode;
	}
	else
	{
		ps->tail->next = newnode;
		ps->tail = newnode;
	}
	//入队后元素数量+1
	ps->size++;
}

//出队
void QueuePop(Que* ps)
{
	assert(ps);
	//检查队列是否为空，若为空则assert函数报错提示
	assert(!QueueEmpty(ps));
	//队列不为空，进行尾删
	//当对列只剩下一个元素时,要注意head和tail指针都要指向NULL，所以为了安全起见，进行分类讨论
	if (ps->head->next == NULL)
	{
		free(ps->head);
		//注意free释放的是该指针指向的空间，而不是释掉该指针
		ps->head = ps->tail = NULL;
	}
	else
	{
		QNode* next = ps->head->next;
		free(ps->head);
		ps->head = next;
	}
	//出队列，元素数量-1
	ps->size--;
}

//取队头
QDatatype QueueFront(Que* ps)
{
	assert(ps);
	//检查队列为不为空
	assert(!QueueEmpty(ps));
	//返回首结点的data域
	return ps->head->data;
}

//取队尾
QDatatype QueueBack(Que* ps)
{
	assert(ps);
	//检查队列为不为空
	assert(!QueueEmpty(ps));
	//返回尾结点的data域
	return ps->tail->data;
}


//判空
bool QueueEmpty(Que* ps)
{
	assert(ps);
	//为空返回真，不为空返回假
	return ps->head == NULL;
}

//获取队列元素个数
int QueueSize(Que* ps)
{
	assert(ps);
	return ps->size;
}






typedef struct {
	Que q1;
	Que q2;
} MyStack;

//栈的初始化
MyStack* myStackCreate() {
	MyStack* pst = (MyStack*)malloc(sizeof(MyStack));
	Queueinit(&pst->q1);
	Queueinit(&pst->q2);
	return pst;
}

//入栈
void myStackPush(MyStack* obj, int x) {
	//根据思路分析，哪个队列不为空，就入队哪个队列
	if (!QueueEmpty(&obj->q1))
	{
		QueuePush(&obj->q1, x);
	}
	else
	{
		QueuePush(&obj->q2, x);
	}
}

//出栈
int myStackPop(MyStack* obj) {
	//根据思路分析，将不为空的队列一的前Size-1个元素导入空队列二；
	//再将不为空的队列一剩余的一个元素出队返回，即为出栈操作；

	//首先我们不知道哪个队列为空，所以我们可以使用“假设法”找出空队列
	Que* empty = &obj->q1;
	Que* noempty = &obj->q2;
	if (!QueueEmpty(&obj->q1))
	{
		empty = &obj->q2;
		noempty = &obj->q1;
	}

	//然后将不为空的队列的前size-1个元素导入空队列
	while (QueueSize(noempty) > 1)
	{
		//取不为空队列的队头，导入空队列
		QueuePush(empty, QueueFront(noempty));
		//不为空队列出队，导入下一个元素
		QueuePop(noempty);
	}

	//到这里，不为空的队列只剩下一个元素，即我们需要出栈的元素；

	//保存该元素
	int top = QueueFront(noempty);
	//出队
	QueuePop(noempty);
	//返回
	return top;
}

//返回栈顶元素
int myStackTop(MyStack* obj) {
	//因为栈为后进先出，队列为先进先出，所以要返回栈顶元素，即返回不为空队列的队尾元素
	if (!QueueEmpty(&obj->q1))
	{
		return QueueBack(&obj->q1);
	}
	else
	{
		return QueueBack(&obj->q2);
	}
}

//栈的判空
bool myStackEmpty(MyStack* obj) {
	//两队列为空，即栈为空，所以直接用逻辑值判断
	return QueueEmpty(&obj->q1) && QueueEmpty(&obj->q2);
}

//栈的销毁
void myStackFree(MyStack* obj) {
	QueueDestroy(&obj->q1);
	QueueDestroy(&obj->q2);
	free(obj);
}

int main()
{
	MyStack pst = {0};
	MyStack* ppst = &pst;
	ppst=myStackCreate(&pst);
	myStackPush(ppst, 1);
	myStackPush(ppst, 2);
	myStackPush(ppst, 3);
	myStackPush(ppst, 4);

	while (!myStackEmpty(ppst))
	{
		printf("%d ", myStackTop(ppst));
		myStackPop(ppst);
	}
	printf("\n");
	myStackFree(ppst);

	return;
}

⭐️2.运行结果：

力扣在线OJ——栈和队列,数据结构与算法,LeetCode,leetcode,算法,c语言,数据结构

🍁二、用栈实现队列

🌕（一）、题目（力扣链接：用栈实现队列）

🌕（二）、思路

第一题是用队列实现栈，而这道题是用栈实现队列，所以两道题有很多相似的地方，小编就快速实现，只要把第一题搞懂了，这道题实现起来非常简单：

①：由第一题我们想到拿一个栈接收数据，一个栈为空，然后在导数据的方式引入思考：

导完数据后：

到这一步当我们再想重复操作时，就发现不同了，因为栈是后进先出，所以导完一次数据后，顺序会返过来，这时，我们只需要依次对q2进行出栈，即可实现队列的先进先出结构：

入队的时候为6 5 4 3 2 1，而这样的操作出队的时候也为 6 5 4 3 2 1；

所以我们会产生一个新的思路：

将q1栈用于存储入队的数据，再将栈q1中的数据出栈，然后入栈到q2中；

当要出队时，只需要对q2进行出栈操作即为出队操作，当q2为空时，就将栈q1中的数据导过来；

把思路理清，图画标准，接下来实现起来就方便多了；

🌕（三）、解答

⭐️1.第一个接口——typedef struct

①：首先我们可以将以前实现过的栈的各个操作复制粘贴进来，没有的小伙伴可以直接看小编的源代码；

②：跟第一题一样，没有栈，我们就定义出两个栈q1和q2；
typedef struct {
	ST q1;
	ST q2;

} MyQueue;

⭐️2.第二个接口——MyQueue* myQueueCreate()

①：意为“初始化操作”,与第一题相同；

//初始化
MyQueue* myQueueCreate() {
	MyQueue* obj = (MyQueue*)malloc(sizeof(MyQueue));
	STinit(&obj->q1);
	STinit(&obj->q2);
	return obj;
}

⭐️3.第三个接口——void myQueuePush(MyQueue* obj, int x)

①：意为“入队操作”；

②：因为栈q1和栈q2的功能是区分开的，所以对于入队操作，我们只需对q1进行入栈操作区即可：
//入队
void myQueuePush(MyQueue* obj, int x) {
	//根据思路分析，我们直接将队列数据入栈到保存栈q1（即两个栈中，负责保存数据的栈）即可
	STPush(&obj->q1, x);
}

⭐️4.第四个接口——int myQueuePop(MyQueue* obj)

①：意为“出队操作”；

②：上面我们都分析过了，只需要按照步骤来即可：

//出队
int myQueuePop(MyQueue* obj) {
	//根据思路分析，我们直接出栈q2即为出队操作，直到q2为空时，再将q1中的数据导入q2

	//先判断q2是否栈空，如果栈空，则将q1的数据导入q2，再出栈
	if (STEmpty(&obj->q2))
	{
		while (!STEmpty(&obj->q1))
		{
			//取q1栈顶元素，入栈到q2
			STPush(&obj->q2, STTop(&obj->q1));
			//q1出栈，以便下次导入数据
			STPop(&obj->q1);
		}
	}
	//因为不仅要出队，还要返回出队元素，所以先取栈顶元素保存，再出栈
	int top = STTop(&obj->q2);
	STPop(&obj->q2);
	return top;
}

⭐️5.第五个接口——int myQueuePeek(MyQueue* obj)

①：意为“取队头操作”；

②：只需要对q2进行出栈并返回即可：


//取队头元素
int myQueuePeek(MyQueue* obj) {
	//根据栈和队列的结构，队头元素即为上述出栈的元素
	//先判断q2是否栈空，如果栈空，则将q1的数据导入q2，再出栈

	//导数据
	if (STEmpty(&obj->q2))
	{
		while (!STEmpty(&obj->q1))
		{
			//取q1栈顶元素，入栈到q2
			STPush(&obj->q2, STTop(&obj->q1));
			//q1出栈，以便下次导入数据
			STPop(&obj->q1);
		}
	}
	return STTop(&obj->q2);
}

⭐️6.第六个接口——bool myQueueEmpty(MyQueue* obj)

①：意为“判断队空操作”；

②：操作与第一题相同：文章来源地址https://www.toymoban.com/news/detail-733790.html
//判断队空
bool myQueueEmpty(MyQueue* obj) {
	//只有当两个栈都为空时，队列才为空
	return STEmpty(&obj->q1) && STEmpty(&obj->q2);
}

⭐️7.第七个接口——void myQueueFree(MyQueue* obj)

①：意为“队列的销毁”；

②：操作与第一题相同：
//销毁
void myQueueFree(MyQueue* obj) {
	//不仅要释放队列,还要销毁两个栈
	STDestroy(&obj->q1);
	STDestroy(&obj->q2);
	free(obj);
}

🌕（四）、第二题源代码


//二、用栈实现队列
typedef int DataType;
typedef struct Stack
{
	DataType* a;
	int top;//指向栈顶
	int catacity;//现有空间大小
}ST;

//初始化
void STinit(ST* ps);

//销毁
void STDestroy(ST* ps);

//入栈
void STPush(ST* ps, DataType x);

//出栈
void STPop(ST* ps);

//获取栈的元素个数
int STSize(ST* ps);

//判断是否为栈空
bool STEmpty(ST* ps);

//获取栈顶元素
DataType STTop(ST* ps);

//初始化
void STinit(ST* ps)
{
	assert(ps);
	//刚开始没有元素，所以top指向0
	ps->top = 0;
	ps->catacity = 0;
	ps->a = NULL;
}

//销毁
void STDestroy(ST* ps)
{
	assert(ps);
	free(ps->a);
	ps->top = 0;
	ps->catacity = 0;
}

//入栈
void STPush(ST* ps, DataType x)
{
	assert(ps);
	//空间满了进行增容
	if (ps->top == ps->catacity)
	{
		//第一次catacity值为0，所以判断一下给予赋值
		int newCatacity = (ps->catacity == 0 ? 4 : ps->catacity * 2);
		//使用realloc函数进行增容，刚开始a为NULL的话realloc函数的作用和malloc相同
		DataType* tmp = realloc(ps->a, sizeof(DataType) * newCatacity);
		//检查是否增容成功
		if (tmp == NULL)
		{
			perror("realloc");
			return;
		}
		ps->a = tmp;
		ps->catacity = newCatacity;
	}
	//插入
	ps->a[ps->top] = x;
	ps->top++;
}

//出栈
void STPop(ST* ps)
{
	assert(ps);
	//ps->top==0时为空栈
	if (0 == ps->top)
	{
		printf("栈为空，出栈失败!\n");
		return;
	}
	//出栈
	--ps->top;
}

//获取栈的元素个数
int STSize(ST* ps)
{
	assert(ps);
	return ps->top;
}

//判断是否为栈空
bool STEmpty(ST* ps)
{
	assert(ps);
	return ps->top == 0;
}

//获取栈顶元素
DataType STTop(ST* ps)
{
	assert(ps);

	if (0 == ps->top)
	{
		printf("栈为空，获取失败!\n");
		exit(-1);
	}
	return ps->a[ps->top - 1];
}

typedef struct {
	ST q1;
	ST q2;

} MyQueue;

//初始化
MyQueue* myQueueCreate() {
	MyQueue* obj = (MyQueue*)malloc(sizeof(MyQueue));
	STinit(&obj->q1);
	STinit(&obj->q2);
	return obj;
}

//入队
void myQueuePush(MyQueue* obj, int x) {
	//根据思路分析，我们直接将队列数据入栈到保存栈q1（即两个栈中，负责保存数据的栈）即可
	STPush(&obj->q1, x);
}

//出队
int myQueuePop(MyQueue* obj) {
	//根据思路分析，我们直接出栈q2即为出队操作，直到q2为空时，再将q1中的数据导入q2

	//先判断q2是否栈空，如果栈空，则将q1的数据导入q2，再出栈
	if (STEmpty(&obj->q2))
	{
		while (!STEmpty(&obj->q1))
		{
			//取q1栈顶元素，入栈到q2
			STPush(&obj->q2, STTop(&obj->q1));
			//q1出栈，以便下次导入数据
			STPop(&obj->q1);
		}
	}
	//因为不仅要出队，还要返回出队元素，所以先取栈顶元素保存，再出栈
	int top = STTop(&obj->q2);
	STPop(&obj->q2);
	return top;
}

//取队头元素
int myQueuePeek(MyQueue* obj) {
	//根据栈和队列的结构，队头元素即为上述出栈的元素
	//先判断q2是否栈空，如果栈空，则将q1的数据导入q2，再出栈

	//导数据
	if (STEmpty(&obj->q2))
	{
		while (!STEmpty(&obj->q1))
		{
			//取q1栈顶元素，入栈到q2
			STPush(&obj->q2, STTop(&obj->q1));
			//q1出栈，以便下次导入数据
			STPop(&obj->q1);
		}
	}
	return STTop(&obj->q2);
}

//判断队空
bool myQueueEmpty(MyQueue* obj) {
	//只有当两个栈都为空时，队列才为空
	return STEmpty(&obj->q1) && STEmpty(&obj->q2);
}

//销毁
void myQueueFree(MyQueue* obj) {
	//不仅要释放队列,还要销毁两个栈
	STDestroy(&obj->q1);
	STDestroy(&obj->q2);
	free(obj);
}

int main()
{
	MyQueue st = { 0 };
	MyQueue* pst = &st;
	pst = myQueueCreate(&st);
	myQueuePush(pst, 1);
	myQueuePush(pst, 2);
	myQueuePush(pst, 3);
	myQueuePush(pst, 4);

	while (!myQueueEmpty(pst))
	{
		printf("%d ", myQueuePeek(pst));
		myQueuePop(pst);

	}
	printf("\n");
	myQueueFree(pst);
	return 0;
}

到了这里，关于力扣在线OJ——栈和队列的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！

力扣在线OJ——栈和队列

🍁一、用两个队列实现栈

🌕（一）、题目（力扣链接：用队列实现栈）

🌕（二）、注意

🌕（三）、解答

⭐️1.注意事项

⭐️2.第一个接口——匿名结构体

⭐️3.第二个接口——MyStack* myStackCreate()

⭐️4.第三个接口——void myStackPush(MyStack* obj, int x)

⭐️5.第四个接口——int myStackPop(MyStack* obj)

⭐️6.第五个接口——int myStackTop(MyStack* obj)

⭐️7.第六个接口——bool myStackEmpty(MyStack* obj)

⭐️8.第七个接口——void myStackFree(MyStack* obj)

🌕（四）、第一题源代码

⭐️1.代码：

⭐️2.运行结果：

🍁二、用栈实现队列

🌕（一）、题目（力扣链接：用栈实现队列）

🌕（二）、思路

🌕（三）、解答

⭐️1.第一个接口——typedef struct

⭐️2.第二个接口——MyQueue* myQueueCreate()

⭐️3.第三个接口——void myQueuePush(MyQueue* obj, int x)

⭐️4.第四个接口——int myQueuePop(MyQueue* obj)

⭐️5.第五个接口——int myQueuePeek(MyQueue* obj)

⭐️6.第六个接口——bool myQueueEmpty(MyQueue* obj)

⭐️7.第七个接口——void myQueueFree(MyQueue* obj)

🌕（四）、第二题源代码

觉得文章有用就打赏一下文章作者

支付宝扫一扫打赏

微信扫一扫打赏

支付宝扫一扫领取红包，优惠每天领

二维码1

二维码2

力扣在线OJ——栈和队列

🍁一、用两个队列实现栈

🌕（一）、题目（力扣链接：用队列实现栈 ）

🌕（二）、注意

🌕（三）、解答

⭐️1.注意事项

⭐️2.第一个接口——匿名结构体

⭐️3.第二个接口——MyStack* myStackCreate()

⭐️4.第三个接口——void myStackPush(MyStack* obj, int x)

⭐️5.第四个接口——int myStackPop(MyStack* obj)

⭐️6.第五个接口——int myStackTop(MyStack* obj)

⭐️7.第六个接口——bool myStackEmpty(MyStack* obj)

⭐️8.第七个接口——void myStackFree(MyStack* obj)

🌕（四）、第一题源代码

⭐️1.代码：

⭐️2.运行结果：

🍁二、用栈实现队列

🌕（一）、题目（力扣链接：用栈实现队列）

🌕（二）、思路

🌕（三）、解答

⭐️1.第一个接口——typedef struct

⭐️2.第二个接口——MyQueue* myQueueCreate()

⭐️3.第三个接口——void myQueuePush(MyQueue* obj, int x)

⭐️4.第四个接口——int myQueuePop(MyQueue* obj)

⭐️5.第五个接口——int myQueuePeek(MyQueue* obj)

⭐️6.第六个接口——bool myQueueEmpty(MyQueue* obj)

⭐️7.第七个接口——void myQueueFree(MyQueue* obj)

🌕（四）、第二题源代码

相关文章

觉得文章有用就打赏一下文章作者

支付宝扫一扫打赏

微信扫一扫打赏

支付宝扫一扫领取红包，优惠每天领

二维码1

二维码2

🌕（一）、题目（力扣链接：用队列实现栈）