Matlab 拉格朗日（lagrange)插值 以及 poly、conv函数理解

https://songshanhu.csdn.net/643f5384986c660f3cf93c13.html?spm=1001.2101.3001.6661.1&utm_medium=distribute.pc_relevant_t0.none-task-blog-2%7Edefault%7EBlogCommendFromBaidu%7Eactivity-1-36407923-blog-83212763.235%5Ev32%5Epc_relevant_increate_t0_download_v2&depth_1-utm_source=distribute.pc_relevant_t0.none-task-blog-2%7Edefault%7EBlogCommendFromBaidu%7Eactivity-1-36407923-blog-83212763.235%5Ev32%5Epc_relevant_increate_t0_download_v2&utm_relevant_index=1

 做笔记，感谢上面链接的老哥！！！！

 一、函数解释

poly   

可以求以向量为解的方程或方阵的特征多项式

1、向量

>> r=[1 2 3]

r =

     1     2     3

>> poly(r)

ans =

     1    -6    11    -6

>> 
 那么求得的方程为：1*x^3+(-6)*x^2+11*x+(-6)=0

2、矩阵

>> A =[-2 1 1 ;0 2 0 ;-4 1 3]

A =

    -2     1     1
     0     2     0
    -4     1     3

>> poly(A)

ans =

     1    -3     0     4

>> 


%=====================================================================

>> A =[1 2 3;4 5 6;7 8 0]

A =

     1     2     3
     4     5     6
     7     8     0

>> poly(A)

ans =

    1.0000   -6.0000  -72.0000  -27.0000


那么方阵A 的特征多项式为  1*x^3+(-6)x^2+(-72)x+(-27)=0

 conv函数：

matlab中conv函数的使用和理解_好好记密码的博客-CSDN博客

计算两个向量的卷积：

创建两个向量并求其卷积。

向量的卷积是什么？？？？

给定两个n维向量α=(a0, a1, …, an-1)T，β=(b0, b1, …, bn-1)T，则α与β的卷积运算定义为：α*β=(c0, c1, …, c2n-2)T，其中

卷积手工计算如下：

  u = [1 2 3];
v = [1 2 3]; 

>> u = [1 2 3];
v = [1 2 3];  %其中w的长度是u和v长度相加减1
w = conv(u,v)

w =

     1     4    10    12     9

>> u = [2 7 3];
v = [1 2 6];  %其中w的长度是u和v长度相加减1
w = conv(u,v)

w =

     2    11    29    48    18





% w 的长度
>> length(w)% length=v+u-1

ans =

     5


%--------------------------------eg2----------------------------------------

>> u = [2 7 3  5];
v = [1 2 6];  %其中w的长度是u和v长度相加减1
w = conv(u,v)

w =

     2    11    29    53    28    30

>> 
>> 

计算两个多项式系数的乘法：

就是那种正常的多项式运算，通过矩阵表示系数，返回运算结果。
如现在要运算(x+2)*(x+3)，可采用如下代码：

手动计算如下：

% 函数原型： (x+2)*(x+3)
>> u=[1 3];
v=[1 2];%行向量表示
>> w=conv(u,v)

w =

     1     5     6

>> w=conv(v,u)

w =

     1     5     6






>> conv([1 3 4],[2 5])

ans =

     2    11    23    20

poly2sym

向量系数的多项式

>> poly2sym([1 0 -2 -5])
 
ans =
 
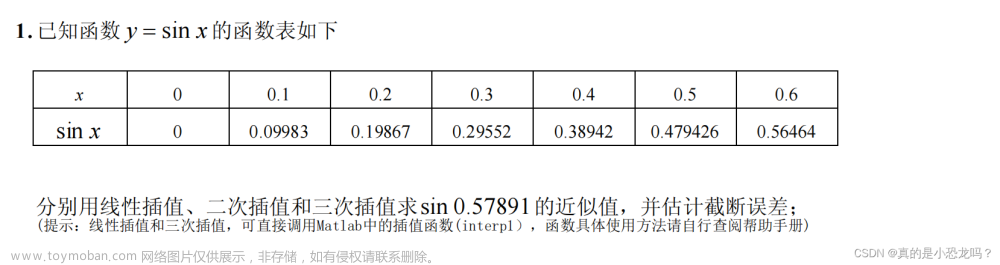
x^3 - 2*x - 5

二、n次拉格朗日插值

定理：

 eg:

  计算步骤：

1、分别计算l0  l1 l2  l3  l4......ln的n次多相式

>> X = [-2, 0, 1, 2]; Y = [17, 1, 2, 17];
p1 = poly(X(1)); p2 = poly(X(2)); p3 = poly(X(3)); p4 = poly(X(4));
l01 = conv(conv(p2, p3), p4)/((X(1) - X(2)) * (X(1) - X(3)) * (X(1) - X(4)));
l11 = conv(conv(p1, p3), p4)/((X(2) - X(1)) * (X(2) - X(3)) * (X(2) - X(4)));
l21 = conv(conv(p1, p2), p4)/((X(3) - X(1)) * (X(3) - X(2)) * (X(3) - X(4)));
l31 = conv(conv(p1, p2), p3)/((X(4) - X(1)) * (X(4) - X(2)) * (X(4) - X(3)));
% 1 分别计算n次的多项式-----------------------------------------------------
l0 = poly2sym(l01), l1 = poly2sym(l11), l2 = poly2sym(l21), l3 = poly2sym(l31)
 
l0 =
 
- x^3/24 + x^2/8 - x/12
 
 
l1 =
 
x^3/4 - x^2/4 - x + 1
 
 
l2 =
 
- x^3/3 + (4*x)/3
 
 
l3 =
 
x^3/8 + x^2/8 - x/4
 

2、计算Pn=y0*l0+y1*l1+ y2*l2+y3*l3+y4*l4+.......+ln*yn

 然后将x=0.6带入到Pn 中

>> l0_1=Y(1)*l0
 
l0_1 =
 
- (17*x^3)/24 + (17*x^2)/8 - (17*x)/12
 
>> l1_1=Y(2)*l1
 
l1_1 =
 
x^3/4 - x^2/4 - x + 1
 
>> l2_1=Y(3)*l2
 
l2_1 =
 
(8*x)/3 - (2*x^3)/3
 
>> l3_1=Y(4)*l3
 
l3_1 =
 
(17*x^3)/8 + (17*x^2)/8 - (17*x)/4
 
>> Pn=l0_1+l1_1+l2_1+l3_1
 
Pn =
 
x^3 + 4*x^2 - 4*x + 1
 
>> 









%=======================================================================================

直接求法

>> P = l01 * Y(1) + l11 * Y(2) + l21 * Y(3) + l31 * Y(4)

P =

     1     4    -4     1

>> L = poly2sym(P), x = 0.6; Y = polyval(P, x)
 
L =
 
x^3 + 4*x^2 - 4*x + 1
 

Y =

    0.2560

>> 

3、计算Rn=f(x)-Pn

4、 

>> syms M; x = 0.6;
R3 = M * abs((x - X(1)) * (x - X(2)) * (x - X(3)) * (x - X(4))) / 24 
 
R3 =
 
(91*M)/2500
 
>> 

手工计算如下：

 Matlab 完整实现：

>> 
X = [-2, 0, 1, 2]; Y = [17, 1, 2, 17];
p1 = poly(X(1)); p2 = poly(X(2)); p3 = poly(X(3)); p4 = poly(X(4));
l01 = conv(conv(p2, p3), p4)/((X(1) - X(2)) * (X(1) - X(3)) * (X(1) - X(4)));
l11 = conv(conv(p1, p3), p4)/((X(2) - X(1)) * (X(2) - X(3)) * (X(2) - X(4)));
l21 = conv(conv(p1, p2), p4)/((X(3) - X(1)) * (X(3) - X(2)) * (X(3) - X(4)));
l31 = conv(conv(p1, p2), p3)/((X(4) - X(1)) * (X(4) - X(2)) * (X(4) - X(3)));
% 1 分别计算n次的多项式-----------------------------------------------------
l0 = poly2sym(l01), l1 = poly2sym(l11), l2 = poly2sym(l21), l3 = poly2sym(l31);

% 2、 P3=sum(y1*l01+     111*y2     +121*y3       +131* y4)  -------------------------------------------
%l0_1=Y(1)*l0;
%l1_1=Y(2)*l1;
%l2_1=Y(3)*l2;
%l3_1=Y(4)*l3;
Pn=l0_1+l1_1+l2_1+l3_1;
P = l01 * Y(1) + l11 * Y(2) + l21 * Y(3) + l31 * Y(4);

	 
% 3、 M = 1*x^3 +4*x^2  +(-4)*x +1 -----------------------------------------------------------------------
L = poly2sym(P), x = 0.6; Y = polyval(P, x);
% 将x=0.6带入M = 1*x^3 +4*x^2  +(-4)*x +1  中 


% 4、R3 =f(x)-P3 =fn+1(v)/(n+1)!  *(x-xn)*(x-x(n-1))*.......*(x-x0)-------------------------------------------------------------
syms M; x = 0.6;
R3 = M * abs((x - X(1)) * (x - X(2)) * (x - X(3)) * (x - X(4))) / 24 
 
l0 =
 
- x^3/24 + x^2/8 - x/12
 
 
l1 =
 
x^3/4 - x^2/4 - x + 1
 
 
l2 =
 
- x^3/3 + (4*x)/3
 
 
L =
 
x^3 + 4*x^2 - 4*x + 1
 
 
R3 =
 
(91*M)/2500
 
>> 

>> 91/2500

ans =

    0.0364

画图：

%画图 
plot(X,Y,'*');
hold on;
y1=polyval(P,X);
plot(X,y1,'color','r');

 * 表示的是用P计算的朗格拉日插值的大概趋势，O表是的是我上面的样本数据

Matlab 代码

%lagran1.m
%求拉格朗日插值多项式和基函数
%输入的量:n+1个节点(x_i,y_i)(i = 1,2, ... , n+1)横坐标向量X，纵坐标向量Y
%输出的量：C 为差值系数
%          L为差值多项式
%          M为矩阵
%          l为各节多项式
function [C,L,M,l] = lagrange_m(X,Y)
m = length(X); 
n = length(Y); 
if m~=n
    return ;
end
M = ones(m,m);% n * n  都为1的矩阵
for k = 1 : m
    V = 1;
    for i = 1 : m
        if k ~= i
            V = conv(V,poly(X(i))) / (X(k) - X(i));
        end
    end
    M(k, :) = V; 
    l(k, :) = poly2sym(V);
end
C = Y * M;
L = Y * l;

test:

X = [-2, 0, 1, 2]; 
Y = [17, 1, 2, 17]; 

>> [C,L,M,l] = lagrange_m(X,Y)

C =

    1.0000    4.0000   -4.0000    1.0000

 
L =
 
x^3 + 4*x^2 - 4*x + 1
 

M =

   -0.0417    0.1250   -0.0833         0
    0.2500   -0.2500   -1.0000    1.0000
   -0.3333         0    1.3333         0
    0.1250    0.1250   -0.2500         0

 
l =
 
- x^3/24 + x^2/8 - x/12
  x^3/4 - x^2/4 - x + 1
      - x^3/3 + (4*x)/3
    x^3/8 + x^2/8 - x/4
 
>> 






% test 


>> x=1.1;polyval(C,x)

ans =

    2.7710

>> x=2.1;polyval(C,x)

ans =

   19.5010

>> 

 拉格朗日插值及其误差估计

%lagrane.m
%拉格朗日插值及其误差估计
%输入的量:X是n+1个节点(x_i,y_i)(i = 1,2, ... , n+1)横坐标向量，Y是纵坐标向量，
%x是以向量形式输入的m个插值点，M在[a,b]上满足｜f~(n+1)(x)｜≤M
%注：f~(n+1)(x)表示f(x)的n+1阶导数
%输出的量：y为m个插值构成的向量，R是误差限
function [y, R] = lagrange_r(X, Y, x, M)
n = length(X);
m = length(x);
for i = 1:m
    z = x(i);
    s = 0.0;
    for k = 1:n
        p = 1.0; q1 = 1.0; c1 = 1.0;
        for j = 1:n
            if j~=k
                p = p * (z - X(j)) / (X(k) - X(j));
            end
            q1 = abs(q1 * (z - X(j)));
            c1 = c1 * j;
        end
        s = p * Y(k) + s;
    end
    y(i) = s;
    R(i) = M * q1 / c1;
end

X = [0 pi/6 pi/4 pi/3 pi/2];
Y = [0 0.5 0.7071 0.8660 1];
x = linspace(0,pi,50);
M = 1;
[y, R] = lagrange_r(X, Y, x, M);
y1 = sin(x);
errorbar(x,y,R,'.g')
hold on
plot(X, Y, 'or', x, y, '.k', x, y1, '-b');
legend('误差','样本点','拉格朗日插值估算','sin(x)');

四、项目测试

clc; 
clear ; 
 cloud=pcread('C:\Users\Albert\Desktop\watch\splicing\part6.pcd');
 X=cloud.Location(:,1);
 % Y=cloud.Location(:,2);
 Z=cloud.Location(:,3);
 X=X';
 Z=Z';
% 
%  X = [-2, 0, 1, 2]; 
%  Z = [17, 1, 2, 17];
 X = [ 4.8429    4.8525    4.8568     ]; 
 Z = [ -1.1626   -1.1862   -1.2122  ];
 plot(X,Z,'*');
 hold on ;
 % sysm  C,L,M,l;
 [C,L,~,~] = lagrange_m(X,Z);
 len=length(X);
 Max=max(X)+0.01;
 Min=min(X);
 x= Min:0.001:Max;
 z=polyval(C,x);
 plot(x,z,'-');

文章来源地址https://www.toymoban.com/news/detail-733906.html

到了这里，关于Matlab 拉格朗日（lagrange)插值 以及 poly、conv函数理解的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！