卡尔曼滤波原理及c++代码实现-Toy模板网

这篇具有很好参考价值的文章主要介绍了卡尔曼滤波原理及c++代码实现。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

最近重新看到了卡尔曼滤波，想把这部分的原理整理写下来。供需要的人理解和学习。
一键三连，点赞收藏关注！

一、定义：

卡尔曼滤波（Kalman filtering）是一种利用线性系统状态方程，通过系统输入输出观测数据，对系统状态进行最优估计的算法，“optimal recursivedata processing algorithm（最优化自回归数据处理算法）”。

卡尔曼滤波不要求信号和噪声都是平稳过程的假设条件。对于每个时刻的系统扰动和观测误差（即噪声），只要对它们的统计性质作某些适当的假定，通过对含有噪声的观测信号进行处理，就能在平均的意义上，求得误差为最小的真实信号的估计值。因此，自从卡尔曼滤波理论问世以来，在通信系统、电力系统、航空航天、环境污染控制、工业控制、雷达信号处理等许多部门都得到了应用，取得了许多成功应用的成果。例如在图像处理方面，应用卡尔曼滤波对由于某些噪声影响而造成模糊的图像进行复原。在对噪声作了某些统计性质的假定后，就可以用卡尔曼的算法以递推的方式从模糊图像中得到均方差最小的真实图像，使模糊的图像得到复原。

二、性质：

（1）卡尔曼滤波是一个算法，它适用于线性、离散和有限维系统。每一个有外部变量的自回归移动平均系统(ARMAX)或可用有理传递函数表示的系统都可以转换成用状态空间表示的系统，从而能用卡尔曼滤波进行计算。

（2）任何一组观测数据都无助于消除x(t)的确定性。增益K(t)也同样地与观测数据无关。

（3）当观测数据和状态联合服从高斯分布时用卡尔曼递归公式计算得到的是高斯随机变量的条件均值和条件方差，从而卡尔曼滤波公式给出了计算状态的条件概率密度的更新过程线性最小方差估计，也就是最小方差估计。

三、算法介绍

卡尔曼滤波器算法：

在这一部分，我们就来描述源于Dr Kalman 的卡尔曼滤波器。下面的描述，会涉及一些基本的概念知识，包括概率（Probability），随机变量（Random Variable），高斯或正态分配（Gaussian Distribution）还有State-space Model等等。但对于卡尔曼滤波器的详细证明，这里不能一一描述。
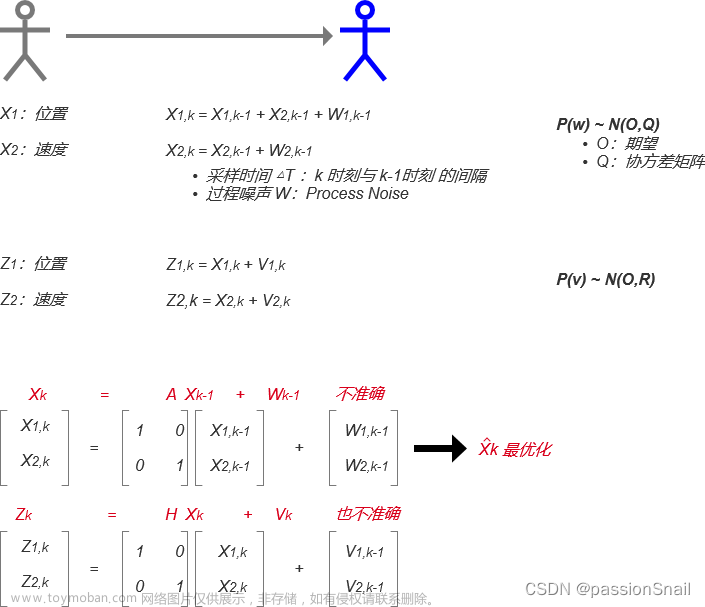
首先，我们先要引入一个离散控制过程的系统。该系统可用一个线性随机微分方程（Linear Stochastic Difference equation）来描述：

X(k)=A X(k-1)+B U(k)+W(k)

再加上系统的测量值：

Z(k)=H X(k)+V(k)

上两式子中，X(k)是k时刻的系统状态，U(k)是k时刻对系统的控制量。A和B是系统参数，对于多模型系统，他们为矩阵。Z(k)是k时刻的测量值，H是测量系统的参数，对于多测量系统，H为矩阵。W(k)和V(k)分别表示过程和测量的噪声。他们被假设成高斯白噪声(White Gaussian Noise)，他们的协方差(covariance)分别是Q，R（这里我们假设他们不随系统状态变化而变化）。
对于满足上面的条件(线性随机微分系统，过程和测量都是高斯白噪声)，卡尔曼滤波器是最优的信息处理器。下面我们结合他们的协方差来估算系统的最优化输出（类似上一节那个温度的例子）。
首先我们要利用系统的过程模型，来预测下一状态的系统。假设现在的系统状态是k，根据系统的模型，可以基于系统的上一状态而预测出现在状态：

X(k|k-1)=A X(k-1|k-1)+B U(k) ……….. (1)

式(1)中，X(k|k-1)是利用上一状态预测的结果，X(k-1|k-1)是上一状态最优的结果，U(k)为现在状态的控制量，如果没有控制量，它可以为0。
到现在为止，我们的系统结果已经更新了，可是，对应于X(k|k-1)的协方差还没更新。我们用P表示协方差(covariance)：

P(k|k-1)=A P(k-1|k-1) A’+Q ……… (2)

X(k|k)= X(k|k-1)+Kg(k) (Z(k)-H X(k|k-1)) ……… (3)

其中Kg为卡尔曼增益(Kalman Gain)：

Kg(k)= P(k|k-1) H’ / (H P(k|k-1) H’ + R) ……… (4)

到现在为止，我们已经得到了k状态下最优的估算值X(k|k)。但是为了要令卡尔曼滤波器不断的运行下去直到系统过程结束，我们还要更新k状态下X(k|k)的协方差：

P(k|k)=（I-Kg(k) H）P(k|k-1) ……… (5)

其中I 为1的矩阵，对于单模型单测量，I=1。当系统进入k+1状态时，P(k|k)就是式子(2)的P(k-1|k-1)。这样，算法就可以自回归的运算下去。

卡尔曼滤波器的原理基本描述了，式子1，2，3，4和5就是他的5 个基本公式。

那么，我们可以理解：使用上一时刻的最优结果预测这一时刻的预测值，同时使用这一时刻观测值（传感器测得的数据）修正这一时刻预测值，得到这一时刻的最优结果。

我们可以不需要累计很久的数据，我们只用上次得到的数据和本次测量的数据即可推算本次数据估计的结果。

c++代码kalman滤波

/** 
 * Write a function 'filter()' that implements a multi-
 *   dimensional Kalman Filter for the example given
 */

#include <iostream>
#include <vector>
// Eigen 部分
#include <Eigen/Core>
#include <Eigen/Dense>

using std::cout;
using std::endl;
using std::vector;
using Eigen::VectorXd;
using Eigen::MatrixXd;

// Kalman Filter variables
VectorXd x;	// object state 障碍物状态矩阵
MatrixXd P;	// object covariance matrix 障碍物不确定性协方差
VectorXd u;	// external motion 外部的运动
MatrixXd F; // state transition matrix 状态转移矩阵
MatrixXd H;	// measurement matrix 测量矩阵
MatrixXd R;	// measurement covariance matrix 测量协方差矩阵
MatrixXd I; // Identity matrix 单位矩阵
MatrixXd Q;	// process covariance matrix 过程协方差矩阵

vector<VectorXd> measurements; // 测量值
void filter(VectorXd &x, MatrixXd &P); // 滤波函数


int main() {
  /**
   * Code used as example to work with Eigen matrices
   */
  // design the KF with 1D motion
  x = VectorXd(2); // 初始化障碍物状态矩阵 第一个为位置，第二个为速度
  x << 0, 0;

  P = MatrixXd(2, 2); // 初始化不确定性协方差矩阵， 刚开始，位置(0,0)的不确定性为1000，速度的不确定性为1000
  P << 1000, 0, 0, 1000;

  u = VectorXd(2); // 运动误差
  u << 0, 0;

  F = MatrixXd(2, 2); // 状态转移矩阵初始化
  F << 1, 1, 0, 1;

  H = MatrixXd(1, 2); // 测量矩阵
  H << 1, 0;

  R = MatrixXd(1, 1); // 测量协方差矩阵
  R << 1;

  I = MatrixXd::Identity(2, 2); // 单位矩阵

  Q = MatrixXd(2, 2); // 过程协方差矩阵
  Q << 0, 0, 0, 0;

  // create a list of measurements
  VectorXd single_meas(1); 
  single_meas << 1;
  measurements.push_back(single_meas);
  single_meas << 2;
  measurements.push_back(single_meas);
  single_meas << 3;
  measurements.push_back(single_meas);

  // call Kalman filter algorithm
  filter(x, P);

  return 0;
}


void filter(VectorXd &x, MatrixXd &P) {

  for (unsigned int n = 0; n < measurements.size(); ++n) {

    VectorXd z = measurements[n];
    // TODO: YOUR CODE HERE
    /**
     * KF Measurement update step
     */
    VectorXd y = z - H * x;
    MatrixXd Ht = H.transpose();
    MatrixXd S = H * P * Ht + R;
    MatrixXd Si = S.inverse();
    MatrixXd K = P * Ht * Si;

    // new state
    x = x + (K * y);
    P = (I - K * H) * P;

    /**
     * KF Prediction step
     */
    x = F * x + u;
    MatrixXd Ft = F.transpose();
    P = F * P * Ft + Q;

    cout << "x=" << endl
         << x << endl;
    cout << "P=" << endl
         << P << endl;
  }
}