前言
hello大家好这里是小L😊， 这学期开启机器学习之旅。在这里想和大家一起学习一起进步。💪
这次笔记内容：学习线性回归的sklearn实现
一、绘制一条直线（普通方法）
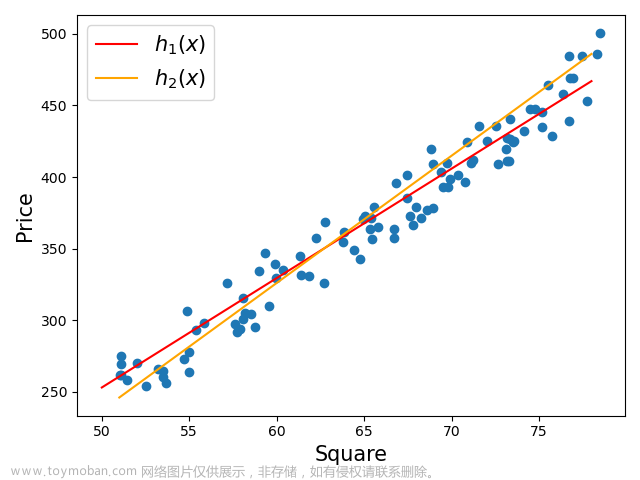
线性回归最后要找的是一条直线
1.通过一段区间绘制一条直线
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
#生成位于区间(-6,6)的等间隔100个点
x=np.linspace(-6,6,100)
#生成对应函数
y=0.5*x+2
#绘制直线图形
plt.plot(x,y,color='red')
2.通过两点绘制一条直线
(1)代码
#已知两点(2,3),(6,5)绘制一条直线
x=np.array([2,6])
y=np.array([3,5])
plt.plot(x,y,marker='d')
(2)求斜率（数学公式）
k=(y[0]-y[1])/(x[0]-x[1])
k
二、线性回归sklearn实现
1.利用sklearn线性回归求直线斜率
sklearn.linear_model.LinearRegression(
)
超参数
- fit_ intercept：截距，是否计算该模型截距。（除非数据标准化之后可false. ）
- normalize：标准化false，标准化一般在建模之前做(sklearn.preprocessing.StandardScale)。
- copy_X：原始的x还在，中间的用另一个存在。如false不要原来的x,新数据覆盖旧数据。
- n_jobs：计算时设置任务点数，若-1最快的速度。
属性
- intercept_ ：截距
- coef_ ：系数Theta0到Theta(n-1),第几个自变量前面的系数，没有截距
方法
- fit 训练
- predict预测
- score模型评估
- get_params返回超参数的值
- set_params修改超参数的值重新训练
x=np.array([2,6])
y=np.array([3,5])
#导入sklearn中的线性回归模块
from sklearn.linear_model import LinearRegression
#线性回归模型实例化
lr=LinearRegression()
#模型训练
x=x.reshape(-1,1)#或者：x=np.array([[2],[6]])二维矩阵两层[],每个自变量x 特征的数目需要一样，并且与y行数相对应
lr.fit(x,y)
print("过两点(2,3)与(6,5)的直线斜率为:{},截距项为:{:.2f}".format(lr.coef_,lr.intercept_))
#模型预测
x_test=np.array([3,4,5]).reshape(-1,1)
y_predict=lr.predict(x_test)
#模型评估——计算R方值（在因变量中占多少比例可由模型解释）
lr.score(x,y)
最终结果为1，完全符合匹配
#计算模型lr均方误差（预测数据与原始数据对应点误差平方和均值）
from sklearn.metrics import mean_squared_error
y=0.5*x_test+2
mean_squared_error(y,y_predict)
最终结果几乎为0，说明模型效果很好。
ps.增加一个点，第三个点(3,6)确定模型
#假设有第3点，坐标为(3,6)
x2=np.array([[2],[6],[3]])
y2=np.array([3,5,6])
#绘制三个点的散点图
plt.scatter(x2,y2,s=180,c='r')
#利用线性回归模型拟合一条均方误差最小的直线
lr2=LinearRegression()
lr2.fit(x2,y2)
y2_predict=lr2.predict(x_test)
y2_predict
print(lr2.coef_,lr2.intercept_)
#拟合出直线
z=np.linspace(0,6,100)
z_predict=lr2.predict(z.reshape(-1,1))
plt.plot(z,z_predict,lw=5,c='g')
plt.scatter(x2,y2,s=180,c='r')
#计算模型lr_2的R方系数
lr_2.score(x2,y2)
#计算模型lr_2的均方误差
from sklearn.metrics import mean_squared_error
mean_squared_error(y2,y2_predict)
二、生成回归模型数据集
1.回归生成器
回归生成器：产生的回归目标作为一个可选择的稀疏线性组合的具有噪声的随机的特征。它的信息特征可能是不相关的或低秩(少数特征占大多数的方差)。
sklearn.datasets.make_regression(
n_samples=100:样本数
n_features=100:特征数（自变量个数）
n_informative=10:参与建模特征数
n_targets=1:因变量个数
noise=0.0:噪音
bias=0.0:偏差（截距）
coef=False:是否输出coef标识
random_state=None:随机状态若为固定值则每次产生的数据都一样
)
#利用sklearn生成100条具有1个特征的回归分析数据集
from sklearn.datasets import make_regression
X_3,y_3=make_regression(n_samples=100,n_features=1)
plt.scatter(X_3,y_3)
X_3,y_3=make_regression(n_samples=100,n_features=1,noise=50,random_state=8)
plt.scatter(X_3,y_3)
2.利用线性回归模型对生成线性回归数据集进行拟合
#利用线性回归模型对数据X_3,y_3进行拟合
reg=LinearRegression()#模型实例化
reg.fit(X_3,y_3)#模型训练
#绘制回归模型
z=linspace(-3,3,200).reshape(-1,1)
plt.scatter(X_3,y_3,c='orangre',s=30)
plt.plot(z,reg.predict(z),c='g')
plt.title('LinearRegression')
print('回归直线的斜率是:{:.2f}'.format(reg.coef_[0]))
print('回归直线的截距是:{:.2f}'.format(reg.intercept_))
由于coef_属性最后输出的为矩阵，因此reg.coef_[0]
三、糖尿病数据集的线性回归分析
1.糖尿病数据集介绍
diabetes是一个关于糖尿病的数据集，该数据集包括442个病人的生理数据及一年后的病情发展状况
2.代码实战
#导入糖尿病数据集
from sklearn.datasets import load_diabetes
diabetes=load_diabetes()
print(diabetes['DESCR'])
X.shape,y.shape
文章来源：https://www.toymoban.com/news/detail-734102.html
#划分训练集和测试集
from sklearn.model_selection import train_test_split
X_train,X_test,y_train,y_test=train_test_split(X,y,random_state=8)
#模型实例化＋标准化
lr=LinearRegression().fit(X_train,y_train)
print("训练数据集得分:{:.2f}".format(lr.score(X_train,y_train)))
print("训练数据集得分:{:.2f}".format(lr.score(X_test,y_test)))
文章来源地址https://www.toymoban.com/news/detail-734102.html
到了这里，关于Python-线性回归的sklearn实现的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
