问题重述
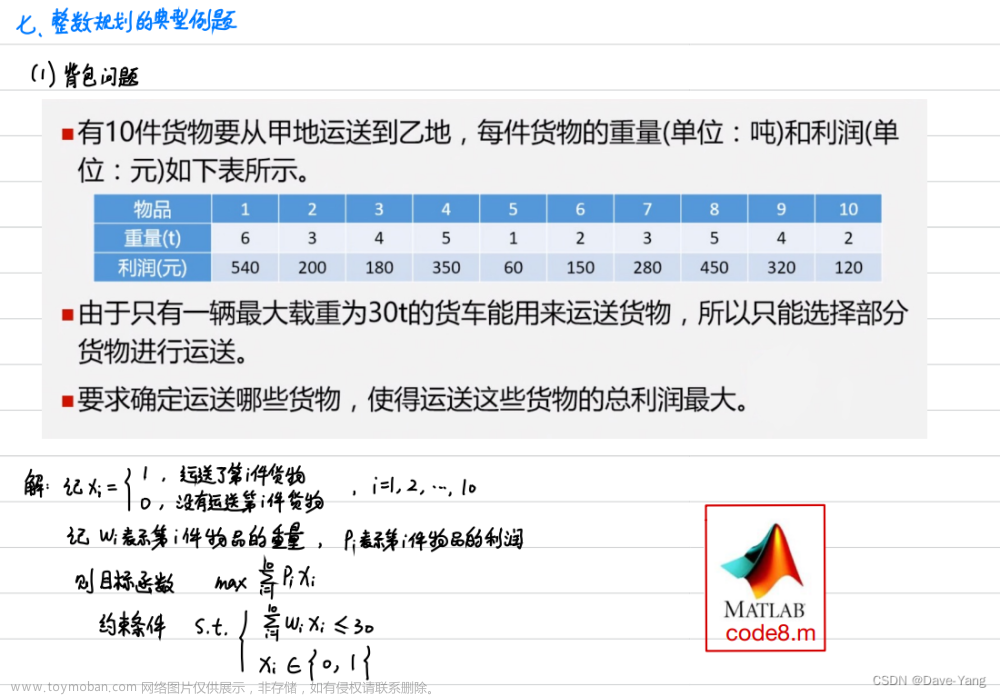
经典解法:整数规划
如图为清风老师讲义中的背包问题 ,其给出的解法为整数规划,代码如下:
%% 背包问题(货车运送货物的问题)
c = -[540 200 180 350 60 150 280 450 320 120]; % 目标函数的系数矩阵(最大化问题记得加负号)
intcon=[1:10]; % 整数变量的位置(一共10个决策变量,均为0-1整数变量)
A = [6 3 4 5 1 2 3 5 4 2]; b = 30; % 线性不等式约束的系数矩阵和常数项向量(物品的重量不能超过30)
Aeq = []; beq =[]; % 不存在线性等式约束
lb = zeros(10,1); % 约束变量的范围下限
ub = ones(10,1); % 约束变量的范围上限
%最后调用intlinprog()函数
[x,fval]=intlinprog(c,intcon,A,b,Aeq,beq,lb,ub)
fval = -fval模拟退火
我尝试了一下用模拟退火求解,也可得到相同的答案,下面为求解过程。模拟退火是一种材料退火过程的仿真优化算法,通过Matropolis准则对随机解进行筛选与迭代,从而完成最优解的求解的方法。
着重介绍一下metropolis准则,这也是模拟退火算法的重点所在。Metropolis 准则在物理上是指在温度下降过程中,粒子的移动产生了新的状态,若新状态的能量更小,则接受新状态,反之,考虑热运动的影响,就以某个概率判断是否接受新状态。在模拟退火算法的搜索过程中,如果算法在某个区域得到了一个适应度值比当前解更差的新解,就使用 Metropolis 准则判断是否接受新解。通过使用 Metropolis 准则,模拟退火算法可以接受较差的解,具备了跳出局部最优陷阱的能力。
对于背包问题,初始解的生成可以采用数组形式,这一点和我之前文章中处理旅行商问题是一样的。不同点在于,此处生成的是0-1序列,因为背包问题解决的根本逻辑是整数规划中的0-1规划。新解的产生只要随机将序列中的0变成1或1变成0即可。这时候便产生一个新的问题,新解中多少个0变成1和多少个1变成0是最有效率的?这也是在该问题中算法优化的主要方向。
参数设定
将各个物理参数和目标参数用类的形式整合在一起,一目了然。模拟退火的外在框架是一个马尔可夫链。每一个温度下,新解的产生都是一个马尔科夫链循环。马尔科夫链即无记忆序列,在同一温度下多次计算可以保证结果的稳定性,但马尔科夫链太长算法的速度便不能保证。其他参数为固体退火基本参数,详细参考模拟退火物理原理,此处不做过多解释。惩罚系数作用于罚函数,此处笔者也不是很了解,一般取1.5。
%% 背包问题
clear;clc
%% 设置求解问题的参数
problem.numVar = 10; %变量个数
problem.fun = @(x)obj_fun(x); %优化目标函数名称
problem.fun_CV = @(x)obj_fun_CV(x); %约束条件
%% 模拟退火的参数
SAParameters.temperature = 100;% 初始温度 设置的足够大的话,可以在初始拥有更好的性能
SAParameters.kb = 0.3; % 温度系数
SAParameters.alpha = 0.9; % 降温系数
SAParameters.penalty = 1.5; % 惩罚系数
SAParameters.num = 100; % 马尔可夫链长度
SAParameters.Tmin = 1; % 结束温度
目标函数
参考0-1规划模型。决策变量x是个长度为10的序列,只包含0或1。0代表不运送该货物;1代表运送该货物。货物价值写在矩阵c中,通过与0-1矩阵的点乘便可求出总价值。具体写法如下:
function f = obj_fun(x) % 目标函数
c = -[540 200 180 350 60 150 280 450 320 120];
f = c.*x;
f = sum(f);
end罚函数
约束条件为所装所有货物重量小于等于30。因此要对货物质量大于30的解进行惩罚。A为各货物的重量矩阵,通过与0-1矩阵的点乘便可求出货物总重量。具体写法如下:
function CV = obj_fun_CV(x) % 约束条件函数
A = [6 3 4 5 1 2 3 5 4 2];
g1 = sum(A.*x)-30;
G1 = (g1>0)*g1; % 大于30时候对其进行惩罚
CV = G1;
end初始解生成
初始解必须是一个可行解,因此全部为1的序列肯定不行,需要对序列进行随机扰动,并且让该序列的解满足罚函数值为0(即满足约束条件)。
%% 解的初始化,产生一个可行解
variables = ones(1,10);
while 1
temp = ceil(rand.*problem.numVar);
variables(temp) = ~variables(temp);
CV = problem.fun_CV(variables);
if CV == 0
break
end
end
var_final = variables; % 初始化最终最优解
T = SAParameters.temperature; % 初始化温度
E0_OBJ = problem.fun(variables); % 初始化目标函数值
E0_CV = problem.fun_CV(variables); % 初始化CV值
E0 = E0_OBJ+SAParameters.penalty*E0_CV; % 最终目标值
E_OBJ_f = E0; % 初始化最佳温度退火过程
通过随机扰动,随机将序列中的1变成0或0变成1,作为新解。此处有很大优化空间,直接决定算法的速度。笔者此处是对整个序列进行随机01变动,但这种方法显然很慢。不过暂时没有想到更好的方法。。。
%% 退火过程
while (T>=SAParameters.Tmin) % 开始降温
for i = 1:SAParameters.num % 马尔科夫链
variables_temp = variables; % 用于暂时存放原来的解
%% 新解的产生,随机扰动法
temp = ceil(rand.*problem.numVar);
variables(temp) = ~variables(temp);
%% 移动后的目标值计算
E_OBJ = problem.fun(variables); % 移动后的目标函数值
E_CV = problem.fun_CV(variables); % 移动后的CV值
E = E_OBJ+SAParameters.penalty*E_CV;
dE = E-E0;
if (E_OBJ<=E_OBJ_f && E_CV==0)
var_final = variables; % 适应度更小且满足约束条件,保留解
E_OBJ_f=E_OBJ;
end
prob=exp(-dE/SAParameters.kb/T);
if(dE>0 && rand()>prob)
variables = variables_temp; % 不满足Metropolis准则,还原解
end
E0_OBJ=problem.fun(variables); %初始目标函数值
E0_CV=problem.fun_CV(variables); %初始CV值
E0=E0_OBJ+SAParameters.penalty*E0_CV;
end
T = T*SAParameters.alpha; % 降温
end
E_OBJ_f = -E_OBJ_f;
总代码
%% 背包问题
clear;clc
%% 设置求解问题的参数
problem.numVar = 10; %变量个数
problem.fun = @(x)obj_fun(x); %优化目标函数名称
problem.fun_CV = @(x)obj_fun_CV(x); %约束条件
%% 模拟退火的参数
SAParameters.temperature = 100;% 初始温度 设置的足够大的话,可以在初始拥有更好的性能
SAParameters.kb = 0.3; % 温度系数
SAParameters.alpha = 0.9; % 降温系数
SAParameters.penalty = 1.5; % 惩罚系数
SAParameters.num = 100; % 马尔可夫链长度
SAParameters.Tmin = 1; % 结束温度
%% 解的初始化,产生一个可行解
variables = ones(1,10);
while 1
temp = ceil(rand.*problem.numVar);
variables(temp) = ~variables(temp);
CV = problem.fun_CV(variables);
if CV == 0
break
end
end
var_final = variables; % 初始化最终最优解
T = SAParameters.temperature; % 初始化温度
E0_OBJ = problem.fun(variables); % 初始化目标函数值
E0_CV = problem.fun_CV(variables); % 初始化CV值
E0 = E0_OBJ+SAParameters.penalty*E0_CV; % 最终目标值
E_OBJ_f = E0; % 初始化最佳温度
%% 退火过程
while (T>=SAParameters.Tmin) % 开始降温
for i = 1:SAParameters.num % 马尔科夫链
variables_temp = variables; % 用于暂时存放原来的解
%% 新解的产生,随机扰动法
temp = ceil(rand.*problem.numVar);
variables(temp) = ~variables(temp);
%% 移动后的目标值计算
E_OBJ = problem.fun(variables); % 移动后的目标函数值
E_CV = problem.fun_CV(variables); % 移动后的CV值
E = E_OBJ+SAParameters.penalty*E_CV;
dE = E-E0;
if (E_OBJ<=E_OBJ_f && E_CV==0)
var_final = variables; % 适应度更小且满足约束条件,保留解
E_OBJ_f=E_OBJ;
end
prob=exp(-dE/SAParameters.kb/T);
if(dE>0 && rand()>prob)
variables = variables_temp; % 不满足Metropolis准则,还原解
end
E0_OBJ=problem.fun(variables); %初始目标函数值
E0_CV=problem.fun_CV(variables); %初始CV值
E0=E0_OBJ+SAParameters.penalty*E0_CV;
end
T = T*SAParameters.alpha; % 降温
end
E_OBJ_f = -E_OBJ_f;
最终结果
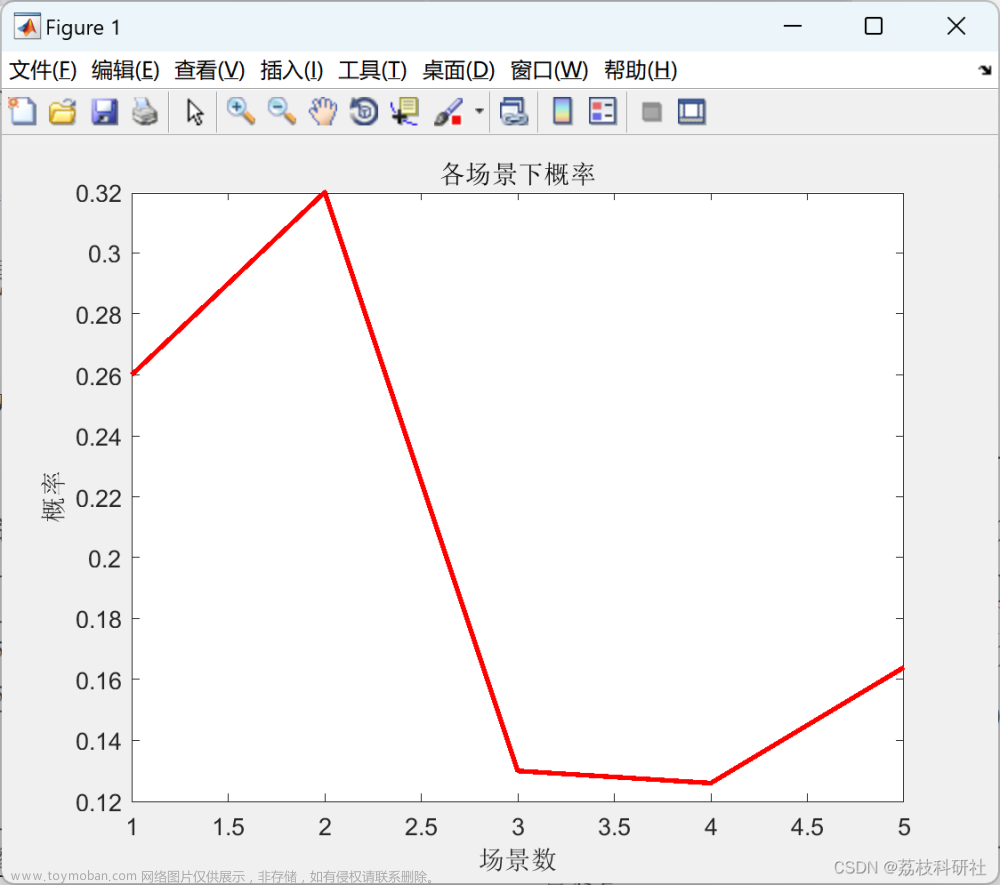
模拟退火结果
这是模拟退火过程求得的结果。

整数规划结果
 文章来源:https://www.toymoban.com/news/detail-734323.html
文章来源:https://www.toymoban.com/news/detail-734323.html
结论
结果相同,证明该模拟退火算法程序是正确的。当然此题比较简单,如果数据更复杂,该算法程序的正确性和效率还有待考察。主要优化空间还在于新解的产生上。笔者在此抛砖引玉,读者若有好想法也可以在评论区交流。文章来源地址https://www.toymoban.com/news/detail-734323.html
到了这里,关于模拟退火解决背包问题的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!