我们经常会碰到几个名词很相近的一些数学术语，例如奇异矩阵、奇异值、奇异值分解、奇异性，经常会混淆，这里把它们的定义放在一起，做一下总结：
1.奇异矩阵：
奇异矩阵是线性代数的概念，就是该矩阵的秩不是满秩。
- 首先，看这个矩阵是不是方阵，即行数和列数相等的矩阵，若行数和列数不相等，那就谈不上奇异矩阵和非奇异矩阵;
- 然后，再看此矩阵的行列式
∣
A
∣
\color{red}|A|
∣A∣是否等于0，若
∣
A
∣
=
0
\color{red}|A|=0
∣A∣=0，称矩阵
A
A
A为
奇异矩阵；若 ∣ A ∣ ≠ 0 \color{red}|A|≠0 ∣A∣=0，称矩阵 A A A为非奇异矩阵。 - 同时，由
∣
A
∣
≠
0
\color{red}|A|≠0
∣A∣=0可知矩阵
A可逆，这样可以得出另外一个重要结论:可逆矩阵就是非奇异矩阵，非奇异矩阵也是可逆矩阵。 - 如果
A
A
A为
奇异矩阵，则 A X = 0 \color{red}AX=0 AX=0 有无穷解， A X = b \color{red}AX=b AX=b 有无穷解或者无解; - 如果
A
A
A为
非奇异矩阵，则 A X = 0 \color{red}AX=0 AX=0 有且只有唯一零解， A X = b \color{red}AX=b AX=b 有唯一解。
2.奇异值和奇异值分解：
这篇博客奇异值的物理意义是什么，是讲解奇异值的作用，有例子分析使用奇异值分解来进行图像压缩与图像去噪，并且对于不是方阵的矩阵也可以分解。
图像压缩与图像去噪用的方法都是奇异值分解，过程也是一样，但是他们的目的不一样：
- 当我们想要
压缩图像进行传输时，我们可以用奇异值分解； - 当我们想要对图像进行
去噪时，我们也可以用奇异值分解；
这就像，我们想要看电影，我们可以使用电脑；我们想要打游戏，我们也可以使用电脑。
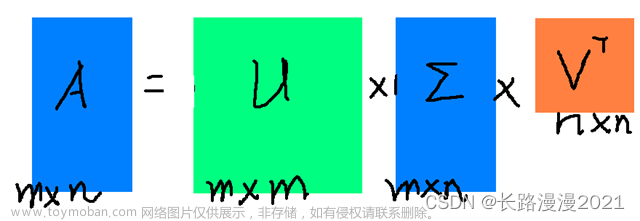
该博客的核心是：
这里做一下说明：
u
u
u、
v
v
v都是列向量，
u
u
u列向量的维度等于
A
m
∗
n
A_{m*n}
Am∗n的行数m、
v
v
v列向量的维度等于
A
A
A的列数n，那么
u
v
T
uv^T
uvT就是 (mx1)*(1xn)=mxn的矩阵，但是
u
v
T
uv^T
uvT的秩必定为1。
例如：
[
1
2
3
]
∗
[
6
7
8
]
=
[
1
∗
6
1
∗
7
1
∗
8
2
∗
6
2
∗
7
2
∗
8
3
∗
6
3
∗
7
3
∗
8
]
\begin{bmatrix} 1\\2\\3\\ \end{bmatrix} * \begin{bmatrix} 6&7&8\\ \end{bmatrix} =\begin{bmatrix} 1*6&1*7&1*8\\2*6&2*7&2*8\\3*6&3*7&3*8\\ \end{bmatrix}
⎣⎡123⎦⎤∗[678]=⎣⎡1∗62∗63∗61∗72∗73∗71∗82∗83∗8⎦⎤
可以看到，上面等式右边的矩阵秩必定为1。
【奇异值分解】 在 【图像压缩】 的运用：
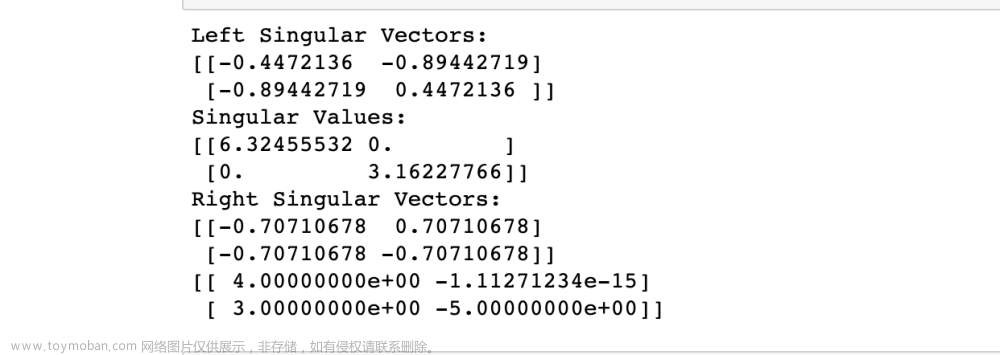
这篇博客奇异值分解是讲解怎么进行SVD奇异值分解，包括求
U
U
U、
V
V
V、奇异值矩阵
Σ
\Sigma
Σ。主要内容如下：
文章来源：https://www.toymoban.com/news/detail-734836.html
3.奇异性：
文章来源地址https://www.toymoban.com/news/detail-734836.html
到了这里，关于【数学与算法】奇异矩阵、奇异值、奇异值分解、奇异性的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
