【Python搜索算法】深度优先搜索（DFS）算法原理详解与应用，示例+代码-Toy模板网

这篇具有很好参考价值的文章主要介绍了【Python搜索算法】深度优先搜索（DFS）算法原理详解与应用，示例+代码。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

1 基本原理

2 DFS算法流程

3 时间复杂度

4 空间复杂度

5 DFS算法应用案例：

5.1 解决路径查找问题

5.2 解决图的连通性问题

5.3 拓扑排序

5.4 在树结构中进行深度遍历

深度优先搜索（DFS）是一种重要的图遍历算法，用于探索图中的节点和边。

1 基本原理

DFS 是一种递归或栈（堆栈）数据结构的算法，用于图的遍历。
从一个起始节点开始，尽可能深入图的分支，直到无法继续深入，然后回溯并探索其他分支。
通过标记已访问的节点来避免重复访问。

2 DFS算法流程

创建一个空的栈（Stack）数据结构，用于存储待访问的节点。

从起始节点开始，将其标记为已访问并入栈。

重复以下步骤，直到栈为空： a. 出栈一个节点，并标记为已访问。 b. 检查该节点的所有未被访问的邻居节点。 c. 对于每个未访问的邻居节点，将其标记为已访问并入栈。

如果无法再继续，即没有未访问的邻居节点，返回上一个节点并继续。

重复步骤2-4，直到遍历整个图。

3 时间复杂度

在最坏情况下，DFS的时间复杂度可以是O(V + E)，其中V是节点数，E是边数。
由于DFS可能访问整个图，因此在稠密图中可能效率较低。

4 空间复杂度

空间复杂度取决于递归深度或堆栈的大小，通常为O(V)

5 DFS算法应用案例：

5.1 解决路径查找问题

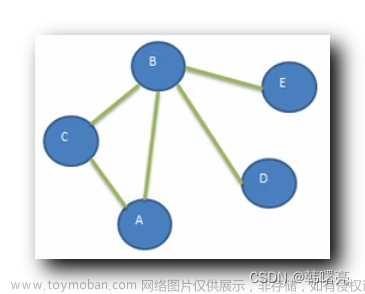
一个常见的应用案例是查找从起始节点到目标节点的路径。例如，在以下示例图中，我们要查找从节点A到节点G的路径。

【Python搜索算法】深度优先搜索（DFS）算法原理详解与应用，示例+代码,Python算法30篇,算法,哈希算法,深度优先

下面是一个简单的Python代码示例，用于执行DFS算法，找到从节点A到节点G的路径。

# 定义示例图
GRAPH = {
    'A': ['B', 'C'],
    'B': ['D', 'E'],
    'C': ['F'],
    'D': [],
    'E': ['F'],
    'F': ['G'],
    'G': []
}

# 定义DFS算法，查找从起始节点到目标节点的路径
def dfs(graph, start, end, path=[]):
    # 将当前节点添加到路径中
    path = path + [start]

    # 如果当前节点等于目标节点，返回找到的路径
    if start == end:
        return path

    # 如果当前节点不在图中，返回None
    if start not in graph:
        return None

    # 遍历当前节点的邻居节点
    for node in graph[start]:
        # 如果邻居节点不在已访问的路径中，继续DFS
        if node not in path:
            new_path = dfs(graph, node, end, path)
            # 如果找到路径，返回该路径
            if new_path:
                return new_path

    # 如果无法找到路径，返回None
    return None

# 调用DFS算法查找从A到G的路径
path = dfs(GRAPH, 'A', 'G')
if path:
    print("Path from A to G:", path)
else:
    print("No path found.")

输出：

【Python搜索算法】深度优先搜索（DFS）算法原理详解与应用，示例+代码,Python算法30篇,算法,哈希算法,深度优先

5.2 解决图的连通性问题：查找下图中的连通组件

【Python搜索算法】深度优先搜索（DFS）算法原理详解与应用，示例+代码,Python算法30篇,算法,哈希算法,深度优先

import networkx as nx
import matplotlib.pyplot as plt

# 定义一个有向图的邻接列表表示
graph = {
    'A': ['B', 'C'],
    'B': ['A'],
    'C': ['A'],
    'D': ['E'],
    'E': ['D'],
    'F': [],
}

def find_connected_components(graph):
    def dfs(node, component):
        visited.add(node)
        component.append(node)
        for neighbor in graph.get(node, []):
            if neighbor not in visited:
                dfs(neighbor, component)

    visited = set()
    connected_components = []

    for node in graph:
        if node not in visited:
            component = []
            dfs(node, component)
            connected_components.append(component)

    return connected_components

# 查找连通组件
components = find_connected_components(graph)

# 打印连通组件
for i, component in enumerate(components, start=1):
    print(f"Connected Component {i}: {component}")

# 创建有向图
G = nx.DiGraph(graph)

# 绘制图形
pos = nx.spring_layout(G)
nx.draw(G, pos, with_labels=True, node_size=500, node_color='lightblue', font_size=10, font_color='black', font_weight='bold')

# 添加边的标签
labels = {}
for node in G.nodes():
    labels[node] = node
edge_labels = {(u, v): v for u, v in G.edges()}
nx.draw_networkx_edge_labels(G, pos, edge_labels=edge_labels, font_size=8)

plt.show()

输出：

【Python搜索算法】深度优先搜索（DFS）算法原理详解与应用，示例+代码,Python算法30篇,算法,哈希算法,深度优先

示例创建 find_connected_components 函数，用于查找图中的连通组件。它使用深度优先搜索（DFS）来遍历图，找到连通组件，并将它们添加到 connected_components 列表中。解析如下：

find_connected_components(graph) 函数接受一个有向图的邻接列表表示为输入，并返回图中的连通组件。

内部嵌套的 dfs(node, component) 函数是深度优先搜索函数。它采用两个参数：

node 表示当前遍历的节点。

component 是一个列表，用于存储当前连通组件中的节点。

dfs 函数的目标是遍历与 node 相关联的节点，并将它们添加到 component 中。

visited 是一个集合，用于跟踪已访问的节点。一开始，它是空的。

connected_components 是一个列表，用于存储找到的连通组件。开始时，它也是空的。

外部的 for 循环遍历图中的每个节点，以确保所有节点都被覆盖。对于每个节点，它执行以下操作：

如果该节点尚未在 visited 中，表示它是一个新的连通组件的起始节点。

创建一个新的空列表 component，用于存储该连通组件的节点。

调用 dfs(node, component) 函数，开始深度优先搜索，并将所有与该节点相连的节点添加到 component 中。

将 component 添加到 connected_components 中，表示已找到一个连通组件。

最后，函数返回 connected_components 列表，其中包含了所有找到的连通组件。

5.3 拓扑排序

拓扑排序是用于确定有向图中节点的线性顺序，使得图中的每一条有向边都是从前面的节点指向后面的节点。在拓扑排序中，没有环路存在。

应用示例：

假设有一个有向图如下，表示课程之间的依赖关系，您需要找到一个可以完成所有课程的顺序。如果存在环路，表示存在无法解决的依赖关系，您需要找到一个没有环路的顺序。

【Python搜索算法】深度优先搜索（DFS）算法原理详解与应用，示例+代码,Python算法30篇,算法,哈希算法,深度优先

import networkx as nx
import matplotlib.pyplot as plt

def topological_sort(graph):
    def dfs(node):
        visited.add(node)
        for neighbor in graph.get(node, []):
            if neighbor not in visited:
                dfs(neighbor)
        result.append(node)

    visited = set()
    result = []

    for node in graph:
        if node not in visited:
            dfs(node)

    return result[::-1]

# 定义有向图的依赖关系
courses = {
    'CSC300': ['CSC100', 'CSC200'],
    'CSC200': ['CSC100'],
    'CSC100': [],
    'CSC400': ['CSC300', 'CSC200'],
}

# 创建一个有向图
G = nx.DiGraph(courses)

# 调用拓扑排序算法
topological_order = topological_sort(courses)

if topological_order:
    print("Topological Order of Courses:", topological_order)
else:
    print("No valid topological order (contains a cycle).")

# 绘制有向图
pos = nx.spring_layout(G)
nx.draw(G, pos, with_labels=True, node_size=500, node_color='lightblue', font_size=10, font_color='black', font_weight='bold')

# 添加边的标签
labels = {}
for node in G.nodes():
    labels[node] = node
edge_labels = {(u, v): v for u, v in G.edges()}
nx.draw_networkx_edge_labels(G, pos, edge_labels=edge_labels, font_size=8)

plt.show()

输出为：

【Python搜索算法】深度优先搜索（DFS）算法原理详解与应用，示例+代码,Python算法30篇,算法,哈希算法,深度优先

示例定义了topological_sort函数，用于执行拓扑排序。这个函数使用深度优先搜索（DFS）来查找图的拓扑排序。如果图中存在环路，该函数仍然会返回一个排序结果，但它不保证是一个有效的拓扑排序。

5.4 在树结构中进行深度遍历

【Python搜索算法】深度优先搜索（DFS）算法原理详解与应用，示例+代码,Python算法30篇,算法,哈希算法,深度优先

import networkx as nx
import matplotlib.pyplot as plt

class TreeNode:
    def __init__(self, value):
        self.value = value
        self.children = []

    def add_child(self, child_node):
        self.children.append(child_node)

def depth_first_search(node, graph, parent=None):
    if node is None:
        return

    graph.add_node(node.value)  # 添加节点到图中

    if parent is not None:
        graph.add_edge(parent.value, node.value)  # 添加边连接父节点和当前节点

    print(node.value)  # 在DFS时输出节点值

    for child in node.children:
        depth_first_search(child, graph, node)  # 递归遍历子节点

# 创建一个较复杂的树结构
root = TreeNode("A")
b = TreeNode("B")
c = TreeNode("C")
d = TreeNode("D")
e = TreeNode("E")
f = TreeNode("F")
g = TreeNode("G")
h = TreeNode("H")
i = TreeNode("I")

root.add_child(b)
root.add_child(c)
b.add_child(d)
b.add_child(e)
c.add_child(f)
c.add_child(g)
g.add_child(h)
h.add_child(i)

# 创建一个有向图
G = nx.DiGraph()

# 执行深度优先搜索并创建图
depth_first_search(root, G)

# 绘制树结构图
pos = nx.spring_layout(G)
nx.draw(G, pos, with_labels=True, node_size=500, node_color='lightblue', font_size=10, font_color='black', font_weight='bold')

# 添加边的标签
labels = {}
for node in G.nodes():
    labels[node] = node
edge_labels = {(u, v): v for u, v in G.edges()}
nx.draw_networkx_edge_labels(G, pos, edge_labels=edge_labels, font_size=8)

plt.show()

这段代码用于创建一个树结构，然后执行深度优先搜索（DFS），最后绘制树结构图并添加标签。以下是对代码的详细解析：

首先，定义了一个树结构的节点类 TreeNode，其中每个节点具有一个值和子节点列表。

在 depth_first_search 函数中，执行深度优先搜索。它接受三个参数：

node：当前要处理的节点。

graph：用于构建树结构图的 NetworkX 有向图对象。

parent：父节点，用于添加边。

在函数中，执行以下操作：

添加当前节点到图中（graph.add_node(node.value)）。

如果存在父节点，添加从父节点到当前节点的边（graph.add_edge(parent.value, node.value)）。

打印当前节点的值，以在DFS期间输出节点值。

递归遍历当前节点的子节点，使用当前节点作为父节点。

创建一个较复杂的树结构：

根节点为 "A"，有两个子节点 "B" 和 "C"。

节点 "B" 有两个子节点 "D" 和 "E"。

节点 "C" 有两个子节点 "F" 和 "G"。

节点 "G" 有一个子节点 "H"。

节点 "H" 有一个子节点 "I"。

创建一个 NetworkX 有向图对象 G，用于存储树结构图。

执行深度优先搜索，从根节点 "A" 开始。深度优先搜索会递归遍历树的每个分支，并在DFS期间输出节点值。

使用 NetworkX 绘制树结构图：

nx.spring_layout 用于确定节点的位置。

nx.draw 用于绘制节点和边，设置节点的大小、颜色和标签。

nx.draw_networkx_edge_labels 用于添加边的标签。

最后，通过 plt.show() 显示绘制的树结构图。文章来源地址https://www.toymoban.com/news/detail-734863.html