数据结构-线性表的链式存储（包含代码实现）

线性表的链式表示和实现

链式存储结构

• 结点在存储器中的位置是任意的，即逻辑上相邻的数据元素在物理上不一定相邻
• 线性表的链式存储结构又称为非顺序映像或链式映像。
• 用一组物理位置任意的存储单元来存放线性表的数据元素
• 这组存储单元既可以是连续的，也可以是不连续的，甚至是零散分布在内存中的任意位置上的。
• 链表中元素的逻辑次序和物理次序不一定相同

与链式存储结构相关的术语
1、结点：数据元素的存储映像。由数据域和指针域两部分组成

• 数据域：存放元素数值数据
• 指针域：存放直接后继结点的存储位置

2、链表：n个结点由指针链组成一个链表

• 它是线性表的链式存储映像，称为线性表的链式存储结构

3、单链表、双链表、循环链表

• 结点只有一个指针域的 链表，称为单链表或线性链表
• 结点有两个指针域的链表，称为双链表
• 首尾相接的链表称为循环链表

4、头指针、头结点和首元结点

• 头指针：是指向链表中第一个结点的指针
  单链表是由表头唯一确定，因此单链表可以用头指针的名字来命名
  若头指针名是L，则把链表称为表L
• 首元结点：是指链表中存储第一个数据元素的结点
• 头结点：是在链表的首元结点之前附设的一个结点

5、链表可分为带头结点和不带头结点

• 无头结点时，头指针为空时表示空表
• 有头结点时，当头指针的指针域为空时表示空表

在链表中设置头结点有什么好处？

• 1、便于首元结点的处理
  首元结点的地址保存在头结点的指针域中，所以在链表的第一个位置上的操作和其他位置上一致，无须进行特殊处理；
• 2、便于空表和非空表的统一处理
  无论链表是否为空，头指针都是指向头结点的非空指针，因此空表和非空表的处理也就统一了。

头结点的数据域内装的是什么？

• 头结点的数据域可以为空，也可以存放线性表长度等附加信息，但此结点不能计入链表长度值

链表（链式存储结构）的特点

• （1）结点在存储器中的位置是任意的，即逻辑上相邻的数据元素在物理上不一定相邻。
• （2）访问时只能通过头指针进入链表，并通过每个结点的指针域依次向后顺序扫描其余结点，（这种存取元素的方法称为顺序存取法）所以寻找第一个结点和最后一个结点所花费的时间不等。

单链表的定义和表示

typedef struct LNode//声明结点的类型和指向结点的指针类型
{
	ElemType date;//结点的数据域
	struct LNode *next;//结点的指针域
}LNode,*LinkList;//LinkList为指向结构体LNode的指针类型

• 定义链表L:LinkList L;
• 定义结点指针p:LNode *p; 也可以LinkList p;
• 重要操作
  p指向头结点： p=L;
  s指向首元结点： s=L->next;
  p指向下一个结点： p=p->next;

单链表基本操作的实现

单链表的初始化

• 即构造一个空表
• 算法步骤
  （1）生成新结点做头指针，用头指针L指向头结点。
  （2）将头结点的指针域置空

判断链表是否为空

• 空表：链表中无元素称为空链表（头指针和头结点仍然存在）
• 算法思路
  判断头结点的指针域是否为空

单链表的销毁

• 链表销毁后不存在
• 算法思路
  从头指针开始，依次释放所有结点

清空链表

• 链表仍然存在，但链表中无元素，成为空链表（头指针和头结点仍然在）

• 算法思路
  依次释放所有结点，并将头结点指针域设置为空

求单链表的表长

• 算法思路
  从首元结点开始，依次计数所有结点

取值–取单链表中第i个元素的内容

• 算法思路
  从链表的头指针出发，顺着链域next逐个结点往下搜索，直至搜索到第i个结点为止。因此，链表不是随机存取结构。

按值查找–根据指定数据获取该数据所在的位置（地址）

• 算法步骤
  1、从第一个结点起，依次和e相比较
  2、如果找到一个其值与e相等的数据元素，则返回其在链表中的“位置”或地址
  3、如果查遍整个链表都没有找到其值与e相等的元素，则返回0或者NULL；

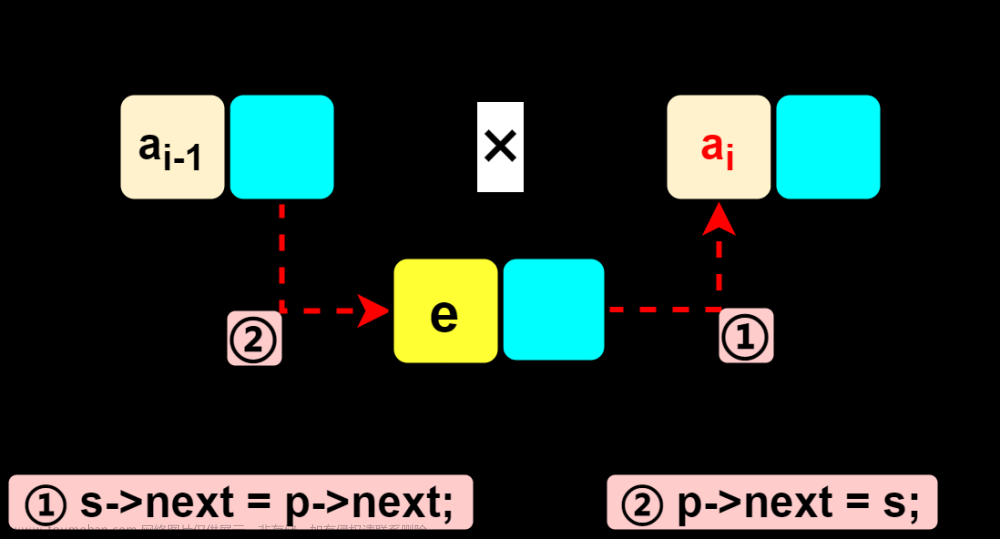
插入–在第i个结点前插入值为e的新结点

• 算法步骤
  1、首先找到i-1个元素的存储位置p
  2、生成一个数据域为e的新结点s
  3、插入新结点：
  ①新结点的指针域指向结点i s->next=p->next;
  ②结点i-1的指针域指向新结点 p->next=s;

删除–删除第i个结点

• 算法步骤
  1、首先找到第i-1的存储位置p，保存要删除的第i个元素的值
  2、令p->next指向原本第i+1个元素
  3、释放原本第i个结点的空间

单链表的查找、插入、删除算法的时间效率分析

• 1、查找：
  因线性链表只能顺序存取，即在查找时要从头指针找起，查找的时间复杂度为O(n)。
• 2、插入和删除
  因线性链表不需要移动元素，只要修改指针，一般情况下时间复杂度为为O(1)。
  但是，如果要在单链表中进行前插或删除操作，由于要从头查找前驱结点，所耗时间复杂度为O(n)。

建立单链表：头插法–元素插入在链表头部，也叫前插法

• 算法步骤
  1、从一个空表开始，重复读入数据
  2、生成新结点，将读入数据存放到新结点的数据域中
  3、从最后一个结点开始，依次将各结点插入到链表的前端

建立单链表：尾插法–元素插入在链表尾部，也叫后插法

• 算法步骤
  1、从一个空表L开始，将新结点逐个插入到链表的尾部，尾指针r指向链表的尾结点。
  2、初始时，r同L一起指向头结点，每读入一个数据元素则申请一个新结点，将新结点插入到尾结点后，r指向新结点

#include<iostream>
using namespace std;

typedef struct student {
	int id;
	struct student* next;
}LNode,*linklist;

int InitList(linklist& L)//初始化一个空链表-
{
	L = new LNode;//或L=(linklist)malloc(sizeof(LNode));
	L->next = NULL;
	return 0;
 }

int ListEmpty(linklist L)//判断是否为空
{
	if (L->next == NULL)//为空
		return 0;
	else
		return 1;
}

void DestroyList(linklist& L)//销毁链表
{
	LNode* p;
	
	while (L)
	{
		p = L;//将p指向头结点
		L = L->next;//指向下一个
		delete p;
	}
}

void ClearList(linklist& L) //清空链表
{
	LNode* p, * q;
	p = L->next;//p指向首元结点
	while (p)//没到表尾
	{
		q = p->next;//q指向p的下一个结点
		delete p;//释放p
		p = q;//p指向下一个结点
	}
	L->next = NULL;//将头结点的指针域置空
}

int ListLength(linklist L)//获取链表长度
{
	linklist p;
	p = L->next;//p指向第一个结点
	int i = 0;
	while (p)//遍历单链表，统计结点数
	{
		i++;
		p = p->next;
	}
	return i;//返回统计的个数i
}

int GetElem(linklist L, int i, int& e)//获取链表中某个位置的元素
{
	LNode* p;
	p = L->next;//p指向首元结点
	int j = 1;//初始化
	while (p && j < i)//向后扫描，直到p指向第i个元素或者p为空
	{
		p = p->next;
		++j;
	}
	if (!p || j > i)//第i个元素不存在
		return -1;
	e = p->id;//取第i个元素的数据域的值
	return 1;
}

LNode* LocateElem(linklist L, int e)//查找某个元素的地址
{
	LNode* p;
	p = L->next;//p指向首元结点
	while (p && p->id != e)//没到尾部并且没找到值为e的结点
	{
		p = p->next;
	}
	return p;//返回找到的结点
}

int LocateELem(linklist L, int e)//根据指定数据查看该数据的位置序号
{
	LNode* p;
	p = L->next;//p指向首元结点
	int j = 1;//初始化计数变量
	while (p && p->id != e)//未到尾部且未找到值为e的结点
	{
		p = p->next;
		j++;
	}
	if (p)
		return j;//找到返回位置序号
	else
		return 0;//没找到返回0

}

int ListInsert(linklist& L, int i, int e)//在指定位置插入数据
{
	linklist p = L;//将p指向头结点
	int j = 0;//初始化计数参数
	while (p && j < i - 1)//寻找第i-1个结点，p指向i-1个结点
	{
		p = p->next;
		++j;
	}
	if (!p || j > i-1)//i大于表长+1或者小于1，插入位置非法
		return -1;
	else
	{
		linklist s;
		//InitList(s);
		s = new LNode;//生成新结点s
		s->id = e;//将结点s的数据域置为e
		s->next = p->next;
		p->next = s;
		return 1;
	}
	
}

int ListDelete(linklist& L, int i,int &e)//删除第i个位置的元素
{
	linklist p= L;
	//InitList(p);
	//p = L;
	int j = 0;//初始化计数变量
	while (p->next && j < i - 1)//寻找第i个结点，并使p指向其前驱，p指向第i-1个结点
	{
		p = p->next;
		++j;
	}
	if (!(p->next) || j > i - 1)//删除位置不合理
	{
		return -1;
	}
	linklist q;
	q = p->next;//q指向第i个结点，临时保存被删结点的地址以备释放

	p->next = q->next;//改变删除结点前驱结点的指针域
	e = q->id;//保存删除结点的数据域
	delete q;//释放删除结点的空间
	return 1;
}

void CreateListHead(linklist& L, int n)//头插
{
	InitList(L);//先建立一个带头结点的单链表
	for (int i = n; i > 0; i--)
	{
		linklist p;//生成新结点p
		p = new LNode;
		cin >> p->id;//输入元素值scanf(&p->id)
		p->next = L->next;//插入到表头
		L->next = p;
	}
}

void CreateListTail(linklist& L, int n)//尾插
{
	InitList(L);
	LNode* r;//新建一个尾指针r
	r = L;//将其指向头结点
	for (int i = 0; i < n; ++i)
	{
		LNode* p;
		p = new LNode;//生成新结点
		cin >> p->id;//输入元素值
		p->next = NULL;//将新插入的结点的指针域置空
		r->next = p;//插入到末尾
		r = p;//r指向新的尾结点
	}
}

void DeleteLinkList(LinkList& L, int e)//删除单链表中某个元素为e的所有结点
{
    Lnode* p, * q;//定义一前一后两个指针
    p = new Lnode;
    q = new Lnode;
    p = L->next;//p指向首元结点
    q = L;//q指向头结点
    while (p)//未到末尾
    {
        if (p->date == e)//查看是否为e
        {
            q->next = p->next;//用q暂存p的下一个结点的地址
            free(p);//释放
            p = q->next;//将p从删除结点的前一个结点指向后面一个
        }
        q = p;//让q指向p
        p = p->next;//p后移一个
    }
}

void PrintLinkList(LinkList L)//输出单链表中的值
{
    Lnode* p;
    p = new Lnode;
    p = L->next;//将p指向首元结点
    while (p)//非空
    {
        cout << p->date << " ";
        p = p->next;
    }
}

int main()
{
	linklist L;
	InitList(L);
	int i=ListLength(L);
	cout <<"插入前元素个数为：" << i << endl;

	CreateListHead(L, 6);
	i = ListLength(L);
	cout << "头插后元素个数为：" << i << endl;

	cout << "头插后元素遍历：" << " ";
	for (int j = 1; j < 7; j++)
	{
		int e_id;
		GetElem(L, j,e_id);
		cout << e_id << " ";
	}
	cout << endl;

	ClearList(L);

	CreateListTail(L, 5);
	i = ListLength(L);
	cout << "尾插后元素个数为：" << i << endl;

	cout << "尾插后元素遍历：" << " ";
	for (int j = 1; j < 6; j++)
	{
		int e_id;
		GetElem(L, j, e_id);
		cout << e_id << " ";
	}
	cout << endl;

	ListInsert(L, 3, 89);

	for (int j = 1; j < 7; j++)
	{
		int e_id;
		GetElem(L, j, e_id);
		cout << e_id << " ";
	}
	cout << endl;

	int e_IDD;
	int result=ListDelete(L, 2, e_IDD);

	cout << "result=" << result << endl;
	for (int j = 1; j < 7; j++)
	{
		int e_id;
		GetElem(L, j, e_id);
		cout << e_id << " ";
	}
	cout << endl;

	return 0;
}

其它链表

循环链表

• 是一种头尾相接的链表（即：表中最后一个结点的指针域指向头结点，整个链表形成一个环）。
• 优点：从表中任一结点出发均可找到表中其它结点。
• 注意：
  由于循环链表中没有NULL指针，故涉及遍历操作时，其终止条件就不再像非循环链表那样判断p或者p->next是否为空，而是判断它们是否等于头指针。
  循环条件 p!=L 或 p->next!=L
• 注意：表的操作常常是在表的首尾位置上进行。

带尾指针的循环链表合并（将Tb合并在Ta之后）

• 步骤：
  1、p存表头节点 p=Ta->next;
  2、Tb表头连接到Ta表尾 Ta->next=Tb->next->next;
  3、释放Tb表头结点 delete Tb->next;
  4、修改指针 Tb->next=p;

//带尾指针的循环链表合并（将Tb合并在Ta之后）
linklist Connect(linklist Ta, linklist Tb)//假设Ta,Tb都是非空的单循环链表
{
	LNode* p;
	p = Ta->next;//p存表头节点
	Ta->next = Tb->next->next;//Tb表头连接到Ta表尾
	delete Tb->next;//释放Tb表头结点 
	Tb->next = p;//修改指针
	return Tb;
}

双向链表

• 在单链表的每个结点里再增加一个指向其直接前驱的指针域prior，这样链表中就形成了有两个方向不同的链，故称为双向链表
• 定义

typedef struct DulNode
{
	Elemtype date;//Elemtype是数据类型
	struct DulNode* prior, * next;
}DulNode,*DuLinkList;

双向循环链表

• 和单链的循环链表类似，双向链表也可以有循环表
  （1）让头结点的前驱指针指向链表最后一个结点
  （2）让最后一个结点的后继指针指向头结点

双向链表结构的对称性

• 设p指向某一结点p->prior->next=p=p->next->peior
• 在双向链表中有些操作，因为仅涉及一个方向的指针，故他们的算法和线性链表的相同。但在插入、删除时，则需要修改两个方向上的指针，两者的操作时间复杂度均为O(n)。

双向链表的插入

int ListInsertDul(DuLinkList& L, int i, Elemtype e)//在带头结点的双向链表L中第i个位置之前插入元素e
{
	DuLinkList p;
	if (!(p = GetElemDul(L, i)))//找到第i个元素，将p指向它，若没找到，返回-1
		return -1;
	
	DuLinkList s;
	s = new DulNode;//新建一个结点
	s->date = e;//给新结点数据域赋值
	s->prior = p->prior;
	p->prior->next = s;
	s->next = p;
	p->prior = s;
	return 1;
}

双向链表的删除

int ListDeleteDul(DuLinkList& L, int i, Elemtype& e)//删除带头结点的双向循环链表L的第i个元素，并用e返回
{
	DuLinkList p;
	if (!(p = GetElemDul(L, i)))//找到第i个元素，将p指向它，若没找到，返回-1
		return -1;
	e = p->date;//将要删除的结点的数据域保存到e中
	p->prior->next = p->next;
	p->next->prior = p->prior;
	free(p);//释放结点
	return 1;
}

总结

链式存储结构的优点

• 结点空间可以动态申请和释放
• 数据元素的逻辑次序靠结点的指针来显示，插入和删除时不需要移动数据元素

链式存储结构的缺点

• 存储密度小，每个结点的指针域需要额外占用内存空间，当每个结点的数据域所占字节不多时，指针域所占用的存储空间的比重显得很大。
• 链式存储结构是非随机存储结构。对于任一结点的操作都要从头指针依指针链查找到该结点，这增加了算法的复杂度

存储密度

• 是指结点数据本身所占的存储量和整个结点结构中所占存储量之比，即
  存储密度=结点数据本身占用的空间/结点占用的空间总量
• 一般的，存储密度越大，存储空间的利用率就越高。显然，顺序表的存储密度为1（100%），而链表的存储密度小于1

单链表、循环链表和双向链表的时间效率比较

顺序表和链表的比较
文章来源地址https://www.toymoban.com/news/detail-734920.html

到了这里，关于数据结构-线性表的链式存储（包含代码实现）的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！