数字图像处理Malab/C++（三）傅里叶变换及频谱图、频域滤波-Toy模板网

这篇具有很好参考价值的文章主要介绍了数字图像处理Malab/C++（三）傅里叶变换及频谱图、频域滤波。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

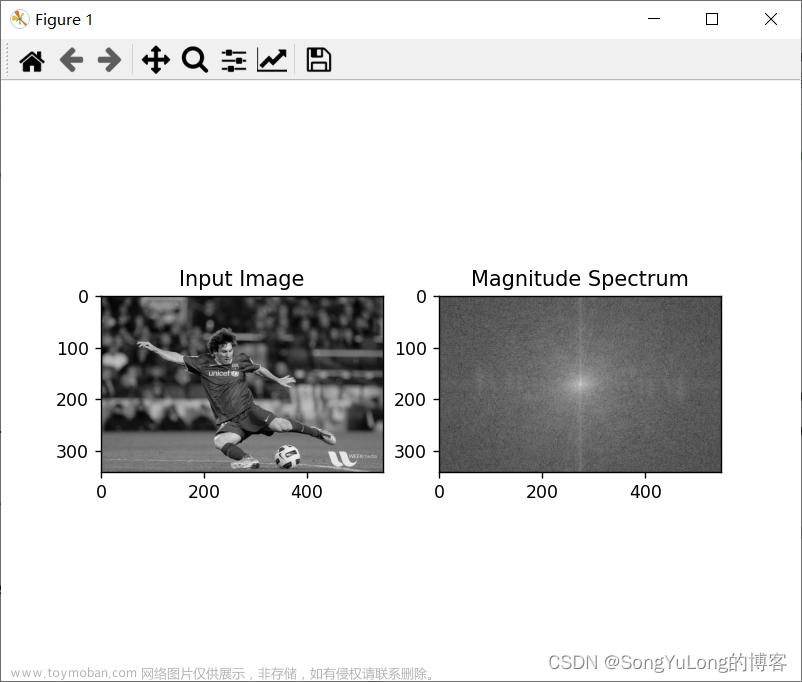
一、Matlab

1、选择任意灰度图像。计算和显示原始图像的频谱振幅和任意因子缩放的同一图像的频谱振幅。

% 1、选择任意灰度图像。计算和显示原始图像的频谱振幅和任意因子缩放的同一图像的频谱振幅。
% 两者之间有什么区别吗，结合课本知识解释这一现象(要求同一窗口显示)？

I = imread('../../std_imgs/lena_gray_256.tif'); %读取灰度图片
I_resize = imresize(I,1/2); %1/2缩放
F = fft2(im2double(I)); F_resize = fft2(im2double(I_resize)); %快速傅里叶变换FFT
F = fftshift(F); F_resize = fftshift(F_resize); %FFT频谱平移
F = abs(F); F_resize = abs(F_resize); %计算幅度谱，
T = log(F+1); T_resize = log(F_resize+1); %频谱对数变换

figure;
subplot(2,2,1),imshow(I);title('原灰度图像');
subplot(2,2,2),imshow(T,[]);title('频谱振幅');
subplot(2,2,3),imshow(I_resize);title('1/2缩放灰度图像');
subplot(2,2,4),imshow(T_resize,[]);title('1/2缩放频谱振幅');

图像处理fft,matlab,图像处理,c++,opencv

2、选择任意灰度图像。计算和显示原始图像的频谱振幅和任意角度旋转的同一图像的频谱振幅。

% 2、选择任意灰度图像。计算和显示原始图像的频谱振幅和任意角度旋转的同一图像的频谱振幅。
% 两者之间有什么区别，结合课本知识解释这一现象(要求同一窗口显示)？

I = imread('../../std_imgs/lena_gray_256.tif'); %读取灰度图片
I_rotate = imrotate(I, 45);
F = fft2(im2double(I)); F_rotate = fft2(im2double(I_rotate)); %快速傅里叶变换FFT
F = fftshift(F); F_rotate = fftshift(F_rotate); %FFT频谱平移
F = abs(F); F_rotate = abs(F_rotate); %计算幅度谱，
T = log(F+1); T_rotate = log(F_rotate+1); %频谱对数变换

figure;
subplot(2,2,1),imshow(I);title('原灰度图像');
subplot(2,2,2),imshow(T,[]);title('频谱振幅');
subplot(2,2,3),imshow(I_rotate);title('逆时针旋转45度灰度图像');
subplot(2,2,4),imshow(T_rotate,[]);title('逆时针旋转45度频谱振幅');

图像处理fft,matlab,图像处理,c++,opencv

3、使用标准Lena灰度图片，添加高斯噪声imnoise(I,‘gaussian’, 0.05) 。请用合适的频域滤波器对图像进行质量提升，获得你认为最好的效果图并计算其峰值信噪比PSNR。（注：PSNR值越高，本题得分越高）

% 3、 使用标准Lena灰度图片，添加高斯噪声imnoise(I,‘gaussian’, 0.05) 。
% 请用合适的频域滤波器对图像进行质量提升，获得你认为最好的效果图并计算其峰值信噪比PSNR。（注：PSNR值越高，本题得分越高）

I = imread('../../std_imgs/lena_gray_256.tif'); %读取标准Lena灰度图片
I_gaussian_noise = imnoise(I,'gaussian', 0.05); %添加高斯噪声

[f_gaussian_noise,revertclass] = tofloat(I_gaussian_noise); 

H1 = lpfilter('ideal',256,256,0.18*256); %频域理想低通滤波器
H2 = lpfilter('butterworth',256,256,0.18*256); %频域巴特沃斯低通滤波器
H3 = lpfilter('gaussian',256,256,0.18*256); %频域高斯低通滤波器

%在频域滤波，傅里叶反变换回图象空间
g1 = dftfilt(f_gaussian_noise,H1); 
g1 = revertclass(g1);
g2 = dftfilt(f_gaussian_noise,H2); 
g2 = revertclass(g2);
g3 = dftfilt(f_gaussian_noise,H3); 
g3 = revertclass(g3);

%计算其峰值信噪比PSNR
peaksnr = psnr(I_gaussian_noise,I);
peaksnr1 = psnr(g1,I);peaksnr2 = psnr(g2,I);peaksnr3 = psnr(g3,I);
fprintf('\n The Peak-SNR value is %0.4f', peaksnr);
fprintf('\n The Peak-SNR1 value is %0.4f', peaksnr1);
fprintf('\n The Peak-SNR2 value is %0.4f', peaksnr2);
fprintf('\n The Peak-SNR3 value is %0.4f', peaksnr3);

figure;
subplot(2,3,1),imshow(I);title('标准Lena灰度图片');
subplot(2,3,2),imshow(I_gaussian_noise,[]);title('添加高斯噪声');
subplot(2,3,3),imshow(g1,[]);title('频域理想低通滤波器');
subplot(2,3,4),imshow(g2,[]);title('频域巴特沃斯低通滤波器');
subplot(2,3,5),imshow(g3,[]);title('频域高斯低通滤波器');

图像处理fft,matlab,图像处理,c++,opencv

4、对标准Lena灰度图片分别使用5x5的高斯核进行空域滤波，结果记为A。实现其对应的频域滤波，结果记为B。分别计算A、B图像的PSNR

% 4、对标准Lena灰度图片分别使用5x5的高斯核进行空域滤波，结果记为A。
% 实现其对应的频域滤波，结果记为B。分别计算A、B图像的PSNR，结合课本知识给出你的结论。

I = imread('../../std_imgs/lena_gray_256.tif'); %读取标准Lena灰度图片

%使用5x5的高斯核进行空域滤波
h1 = fspecial('gaussian',[5 5],0.5);
h2 = fspecial('gaussian',[5 5],1);
h3 = fspecial('gaussian',[5 5],2);
A1 = imfilter(I,h1,'replicate'); 
A2 = imfilter(I,h2,'replicate'); 
A3 = imfilter(I,h3,'replicate'); 

%频域高斯低通滤波
[f,revertclass] = tofloat(I); 
H1 = lpfilter('gaussian',256,256,0.15*256); 
H2 = lpfilter('gaussian',256,256,0.18*256); 
H3 = lpfilter('gaussian',256,256,0.23*256); 
g1 = dftfilt(f,H1); 
B1 = revertclass(g1);
g2 = dftfilt(f,H2); 
B2 = revertclass(g2);
g3 = dftfilt(f,H3); 
B3 = revertclass(g3);

%计算其峰值信噪比PSNR
peaksnrA1 = psnr(A1,I);peaksnrA2 = psnr(A2,I);peaksnrA3 = psnr(A3,I);
peaksnrB1 = psnr(B1,I);peaksnrB2 = psnr(B2,I);peaksnrB3 = psnr(B3,I);
fprintf('\n The Peak-SNRA value is %0.4f %0.4f %0.4f', peaksnrA1,peaksnrA2,peaksnrA3);
fprintf('\n The Peak-SNRB value is %0.4f %0.4f %0.4f', peaksnrB1,peaksnrB2,peaksnrB3);

figure;
subplot(1,3,1),imshow(I);title('标准Lena灰度图片');
subplot(1,3,2),imshow(A2,[]);title('5x5的高斯核空域滤波');
subplot(1,3,3),imshow(B2,[]);title('频域高斯低通滤波');

图像处理fft,matlab,图像处理,c++,opencv 文章来源地址https://www.toymoban.com/news/detail-735057.html

二、C++

//1、选择任意灰度图像。计算和显示原始图像的频谱振幅和任意因子缩放的同一图像的频谱振幅。两者之间有什么区别吗，结合课本知识解释这一现象(要求同一窗口显示)？
//2、选择任意灰度图像。计算和显示原始图像的频谱振幅和任意角度旋转的同一图像的频谱振幅。两者之间有什么区别，结合课本知识解释这一现象(要求同一窗口显示)？
//3、 使用标准Lena灰度图片，添加高斯噪声imnoise(I, ‘gaussian’, 0.05) 。请用合适的频域滤波器对图像进行质量提升，获得你认为最好的效果图并计算其峰值信噪比PSNR。（注：PSNR值越高，本题得分越高）
//4、对标准Lena灰度图片分别使用5x5的高斯核进行空域滤波，结果记为A。实现其对应的频域滤波，结果记为B。分别计算A、B图像的PSNR，结合课本知识给出你的结论。

#include<opencv2/opencv.hpp>
#include<iostream>

using namespace cv;
using namespace std;


//定义傅里叶变换函数。input_image：输入图像；output_image：傅里叶频谱图；transform_array:傅里叶变换矩阵（复数）
void My_DFT(Mat input_image, Mat& output_image, Mat& transform_array);


int main()
{
	Mat ori_gray_image, out_gray_image1, out_gray_image2, out_gray_image3, out_gray_image4;

	ori_gray_image = imread("..\\..\\std_imgs\\lena_gray_256.tif", IMREAD_GRAYSCALE);

	//检测图像是否加载成功
	if (ori_gray_image.empty())
	{
		cout << "Could not open or find the image" << endl;
		return -1;
	}

	//显示原图像
	imshow("ori_gray_image", ori_gray_image);

	//傅里叶变换，image_output为可显示的频谱图，image_transform为傅里叶变换的复数结果
	Mat ori_gray_spec, ori_gray_reansform;
	My_DFT(ori_gray_image, ori_gray_spec, ori_gray_reansform);
	imshow("ori_gray_spec", ori_gray_spec);

	//1/8缩放
	resize(ori_gray_image, out_gray_image1, Size(), 1.0 / 8, 1.0 / 8);
	imshow("out_gray_image1", out_gray_image1);

	//旋转
	Point2f center(0.5 * ori_gray_image.rows, 0.5 * ori_gray_image.cols);
	Mat M = getRotationMatrix2D(center,45.0,0.707); //计算二维旋转的仿射矩阵
	warpAffine(ori_gray_image, out_gray_image2, M, Size()); //对图像应用仿射变换。
	imshow("out_gray_image2", out_gray_image2);

	waitKey(0);

	return 0;
}

//傅里叶变换得到频谱图和复数域结果
void My_DFT(Mat input_image, Mat& output_image, Mat& transform_image)
{
	//1.扩展图像矩阵，为2，3，5的倍数时运算速度快
	int m = getOptimalDFTSize(input_image.rows);
	int n = getOptimalDFTSize(input_image.cols);
	copyMakeBorder(input_image, input_image, 0, m - input_image.rows, 0, n - input_image.cols, BORDER_CONSTANT, Scalar::all(0));

	//2.创建一个双通道矩阵planes，用来储存复数的实部与虚部
	Mat planes[] = { Mat_<float>(input_image), Mat::zeros(input_image.size(), CV_32F) };

	//3.从多个单通道数组中创建一个多通道数组:transform_image。函数Merge将几个数组合并为一个多通道阵列，即输出数组的每个元素将是输入数组元素的级联
	merge(planes, 2, transform_image);

	//4.进行傅立叶变换
	dft(transform_image, transform_image);

	//5.计算复数的幅值，保存在output_image（频谱图）
	split(transform_image, planes); // 将双通道分为两个单通道，一个表示实部，一个表示虚部
	magnitude(planes[0], planes[1], output_image); //计算复数的幅值，保存在output_image（频谱图）

	//6.前面得到的频谱图数级过大，不好显示，因此转换
	output_image += Scalar(1);   // 取对数前将所有的像素都加1，防止log0
	log(output_image, output_image);   // 取对数
	normalize(output_image, output_image, 0, 1, NORM_MINMAX); //归一化

	//7.剪切和重分布幅度图像限
	output_image = output_image(Rect(0, 0, output_image.cols & -2, output_image.rows & -2));

	// 重新排列傅里叶图像中的象限，使原点位于图像中心
	int cx = output_image.cols / 2;
	int cy = output_image.rows / 2;
	Mat q0(output_image, Rect(0, 0, cx, cy));   // 左上区域
	Mat q1(output_image, Rect(cx, 0, cx, cy));  // 右上区域
	Mat q2(output_image, Rect(0, cy, cx, cy));  // 左下区域
	Mat q3(output_image, Rect(cx, cy, cx, cy)); // 右下区域

	  //交换象限中心化
	Mat tmp;
	q0.copyTo(tmp); q3.copyTo(q0); tmp.copyTo(q3);//左上与右下进行交换
	q1.copyTo(tmp); q2.copyTo(q1); tmp.copyTo(q2);//右上与左下进行交换
}

到了这里，关于数字图像处理Malab/C++（三）傅里叶变换及频谱图、频域滤波的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！