2D游戏若想模仿3D游戏的环境,一种很好的方案便是“2.5D”。
所谓2.5D,通常的理解是相机固定俯视的游戏视角。在此视角下,人物可以在x、y、z三个轴上移动,如此便能模仿3D游戏的环境,而美术成本要比3D低很多。
2.5D具体实现的方式也分多种,如2D角色+3D场景、3D角色+2D场景贴图、2D角色+2D场景贴图。此文章讨论对象为最后一种,由于角色和场景都采用2D图片,所以本质仍可以归为2D游戏。
Demo演示:

Vector3 v3=new Vector3();
float pi=3.14159265f;
float pi_180=pi/180;
if(performer!=null)
{
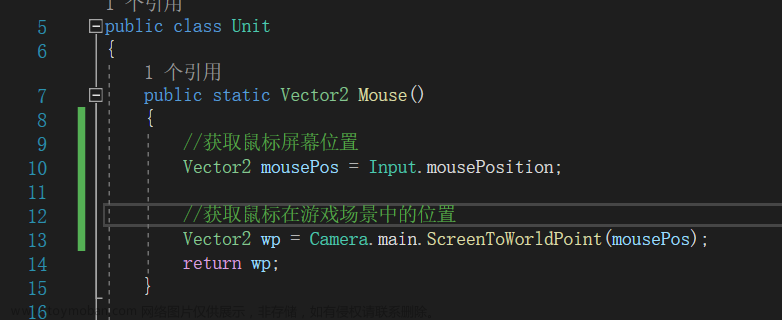
v3[0] = ((float)x);//和本体相同
v3[1] = ((float)(Mathf.Cos(30 * pi_180)*y+Mathf.Sin(30 * pi_180)*z));//将三维坐标映射给二维贴图,其中30是根据2D图片假设的相机角度,pi_180是将角度转换成弧度进行计算。
v3[2] = ((float)z*0.01f);//用于控制遮挡顺序,和本体成正比即可
performer.transform.position=v3;
}
此处采用了一种简单的方法:将人物本体(逻辑)和人物贴图(表现)分离,通过三角函数算出人物贴图在2D场景中的位置。
假设相机角度为α,人物贴图的位置为(x2,y2),人物逻辑的位置为(x,y,z),可知:
x2=x
y2=cos(α)*y+sin(α)*z
如此便在2D视角下模拟出了一个三维世界,而在此基础上,还可以利用unity本身的物理系统设计出3D地形,从而实现斜坡、拱桥等功能。效果图如下:


由于人物本体仍处于3D空间中,因此可以直接在3D空间加入碰撞体来实现地形(可以看到碰撞体和贴图之间并不贴合,之后会解释原因)


那么要怎样根据2D贴图去制作碰撞体呢?之前有提到三维映射到二维的公式,那么反过来,从二维映射到三维也是可以的。但是二维上的一个点映射到三维会有无限种可能,直接套用公式并不可行,因此只能先假定y或z为一个固定值,通过另一值的变化量来计算相对坐标。
设相机角度为α,贴图的点位为(x2,y2),逻辑的点位为(x,y,z),一个格子为一个单位
 如图,Δz=0,Δy2≈1.92
如图,Δz=0,Δy2≈1.92
套公式得Δy2=cosα*Δy+sinα*0,得y=y2/cosα,此时我设置的α为30°,所以Δy≈2.217

同理,得Δz≈5.688
 套用在碰撞体上即可
套用在碰撞体上即可
可以发现映射后的y已经比二维上的y更大了,所以在二维视角下碰撞体和贴图并不贴合

↑宽度测试,符合预期结果

对于坡道的角度也要以同样的方式处理,三维坡角=二维坡角/cosα,此处相机角度为30°,坡道贴图的角度为15°,碰撞体的坡角即是17.32°。
拱桥则套用椭圆公式,x^2/a^2+ (y/cosα)^2/b^2 = 1
搭建好场景后,还需设置角色上坡和投射影子的逻辑,详情可看此篇文章:文章来源:https://www.toymoban.com/news/detail-735906.html
Unity 对角色上坡的研究__独孤星夜_的博客-CSDN博客文章来源地址https://www.toymoban.com/news/detail-735906.html
到了这里,关于Unity 2D视角下模拟3D环境和地形的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!