树是一种常见的数据结构,它在计算机科学和数学中都有广泛的应用。树结构的最简单形式是二叉树,本文将深入探讨树和二叉树的概念、存储结构以及二叉树的遍历,并提供一些实际的代码示例来帮助理解这些概念。

树与二叉树的概念
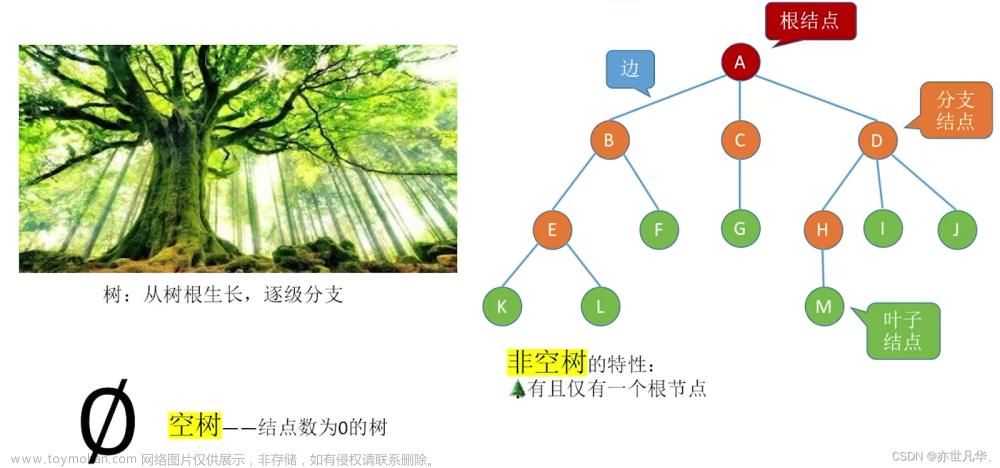
树 (Tree)
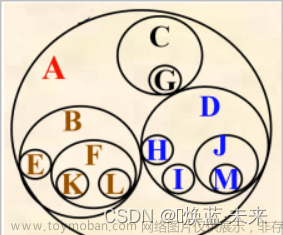
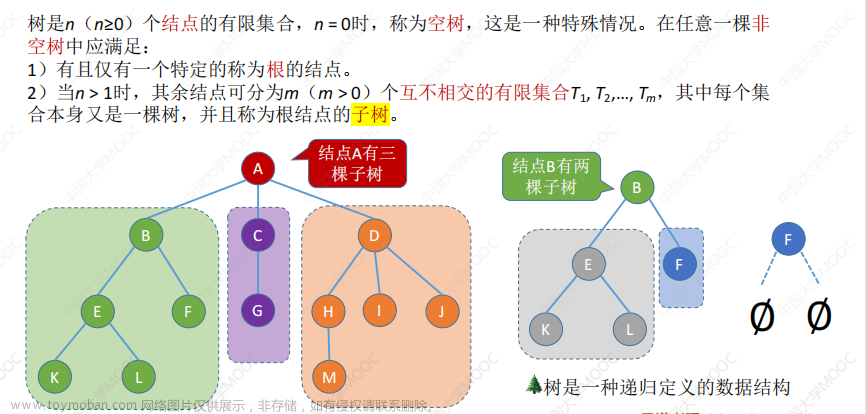
树是一种层次性数据结构,由节点(或称为顶点)和边组成。树的一个特点是它没有环路,即不存在从一个节点出发经过若干边后再回到原节点的路径。树通常包括一个根节点,它没有父节点,以及若干子树,每个子树也是一个树。树中的节点分为内部节点和叶节点,内部节点具有子节点,而叶节点没有子节点。
二叉树 (Binary Tree)
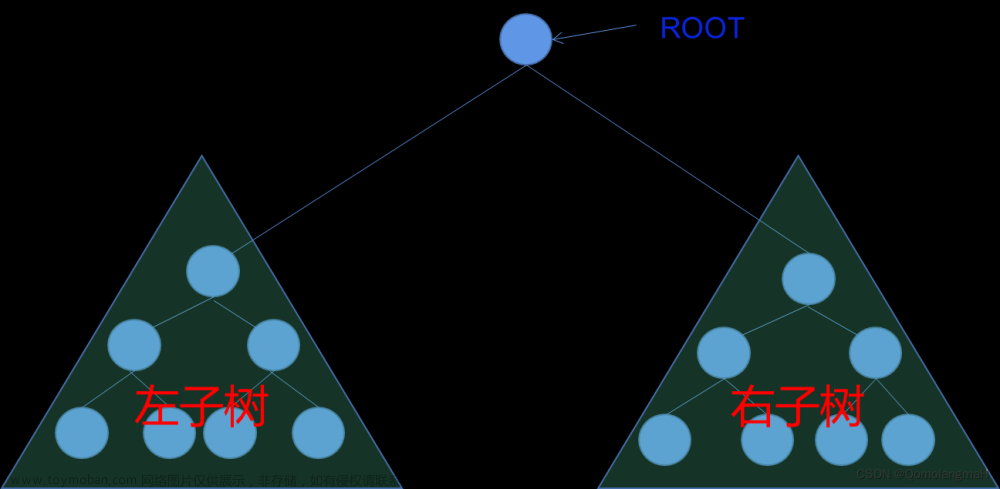
二叉树是一种特殊的树结构,每个节点最多有两个子节点,通常称为左子节点和右子节点。二叉树有多种变体,包括二叉搜索树(Binary Search Tree)和平衡二叉树(Balanced Binary Tree),它们在数据存储和检索方面具有重要的应用。
树与二叉树的存储结构
树和二叉树可以以多种方式进行存储,最常见的方法是使用节点和引用链接的方式。以下是一个简单的二叉树节点的定义:
struct BinaryTreeNode {
int data;
BinaryTreeNode* left;
BinaryTreeNode* right;
BinaryTreeNode(int value) : data(value), left(nullptr), right(nullptr) {}
};
每个节点包含一个数据元素和指向左子节点和右子节点的指针。通过这种方式,可以递归地构建整个二叉树结构。
二叉树的遍历
树的遍历是指按照一定规则访问树中的所有节点,以便查找、处理或打印它们的值。常用的二叉树遍历方法包括前序遍历、中序遍历和后序遍历。
1. 前序遍历 (Preorder Traversal)
前序遍历从根节点开始,按照根-左-右的顺序遍历节点。以下是递归和非递归的C++代码示例:
递归方式:
void preorderTraversal(BinaryTreeNode* node) {
if (node != nullptr) {
cout << node->data << " "; // 先访问根节点
preorderTraversal(node->left); // 再访问左子树
preorderTraversal(node->right); // 最后访问右子树
}
}
非递归方式(使用栈):
#include <stack>
void iterativePreorderTraversal(BinaryTreeNode* root) {
if (root == nullptr) return;
stack<BinaryTreeNode*> nodeStack;
nodeStack.push(root);
while (!nodeStack.empty()) {
BinaryTreeNode* current = nodeStack.top();
nodeStack.pop();
cout << current->data << " "; // 访问当前节点
if (current->right != nullptr) {
nodeStack.push(current->right); // 先将右子节点入栈
}
if (current->left != nullptr) {
nodeStack.push(current->left); // 再将左子节点入栈
}
}
}
2. 中序遍历 (Inorder Traversal)
中序遍历按照左-根-右的顺序遍历节点。以下是递归和非递归的C++代码示例:
递归方式:
void inorderTraversal(BinaryTreeNode* node) {
if (node != nullptr) {
inorderTraversal(node->left); // 先访问左子树
cout << node->data << " "; // 再访问根节点
inorderTraversal(node->right); // 最后访问右子树
}
}
非递归方式(使用栈):
void iterativeInorderTraversal(BinaryTreeNode* root) {
stack<BinaryTreeNode*> nodeStack;
BinaryTreeNode* current = root;
while (current != nullptr || !nodeStack.empty()) {
while (current != nullptr) {
nodeStack.push(current);
current = current->left;
}
current = nodeStack.top();
nodeStack.pop();
cout << current->data << " "; // 访问当前节点
current = current->right;
}
}
3. 后序遍历 (Postorder Traversal)
后序遍历按照左-右-根的顺序遍历节点。以下是递归和非递归的C++代码示例:
递归方式:
void postorderTraversal(BinaryTreeNode* node) {
if (node != nullptr) {
postorderTraversal(node->left); // 先访问左子树
postorderTraversal(node->right); // 再访问右子树
cout << node->data << " "; // 最后访问根节点
}
}
非递归方式(使用两个栈):
void iterativePostorderTraversal(BinaryTreeNode* root) {
if (root == nullptr) return;
stack<BinaryTreeNode*> s1, s2;
s1.push(root);
while (!s1.empty()) {
BinaryTreeNode* current = s1.top();
s1.pop();
s2.push(current);
if (current->left != nullptr) {
s1.push(current->left);
}
if (current->right != nullptr) {
s1.push(current->right);
}
}
while (!s2.empty()) {
BinaryTreeNode* current = s2.top();
s2.pop();
cout << current->data << " "; // 访问当前节点
}
}
示例与分析
考虑以下二叉树:手画不好看,用空格敲出来的。
1
/ \
2 3
/ \
4 5
对该二叉树进行前序、中序和后序遍历的C++代码示例如下:
int main() {
BinaryTreeNode* root = new BinaryTreeNode(1);
root->left = new BinaryTreeNode(2);
root->right = new BinaryTreeNode(3);
root->left->left = new BinaryTreeNode(4);
root->left->right = new BinaryTreeNode(5);
cout << "前序遍历:";
preorderTraversal(root);
cout << endl;
cout << "中序遍历:";
inorderTraversal(root);
cout << endl;
cout << "后序遍历:";
postorderTraversal(root);
cout << endl;
return 0;
}
这些遍历方法将输出以下结果:
前序遍历: 1 2 4 5 3
中序遍历: 4 2 5 1 3
后序遍历: 4 5 2 3 1
换句话说,三种二叉树遍历方式是根节点在不同位置的遍历方式,它们在处理二叉树时具有不同的应用场景和用途。让我们更详细地讨论一下这三种遍历方式:
-
前序遍历 (Preorder Traversal):前序遍历从根节点开始,然后按照根-左-右的顺序遍历节点。在前序遍历中,首先访问根节点,然后递归地访问左子树,最后递归地访右子树。这种遍历方式通常用于创建树的副本或表达式求值。
-
中序遍历 (Inorder Traversal):中序遍历按照左-根-右的顺序遍历节点。在中序遍历中,首先递归地访问左子树,然后访问根节点,最后递归地访问右子树。这种遍历方式通常用于获取二叉搜索树的元素按升序排列。
-
后序遍历 (Postorder Traversal):后序遍历按照左-右-根的顺序遍历节点。在后序遍历中,首先递归地访问左子树,然后递归地访问右子树,最后访问根节点。这种遍历方式通常用于释放树的内存或执行某些计算。文章来源:https://www.toymoban.com/news/detail-735945.html
这些C++代码示例清晰展示了如何创建一个二叉树,以及如何使用递归和非递归方式执行前序、中序和后序遍历。这些遍历方法在不同的应用中具有不同的用途,例如前序遍历可以用于复制整个树结构,中序遍历用于获取有序数据,后序遍历常用于计算表达式树。文章来源地址https://www.toymoban.com/news/detail-735945.html
到了这里,关于C/C++数据结构之深入了解树与二叉树:概念、存储结构和遍历的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!