70. 爬楼梯

8月前作者：Coding+_+ 分类：Toy博客阅读(16) 违法举报

这篇具有很好参考价值的文章主要介绍了70. 爬楼梯。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

假设你正在爬楼梯。需要 n 阶你才能到达楼顶。

每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？

示例 1：

输入：n = 2
输出：2
解释：有两种方法可以爬到楼顶。
1. 1 阶 + 1 阶
2. 2 阶

示例 2：

输入：n = 3
输出：3
解释：有三种方法可以爬到楼顶。
1. 1 阶 + 1 阶 + 1 阶
2. 1 阶 + 2 阶
3. 2 阶 + 1 阶

提示：文章来源地址https://www.toymoban.com/news/detail-736297.html

1 <= n <= 45

class Solution {
public:
    int climbStairs(int n) {
        if(n < 2) return n;
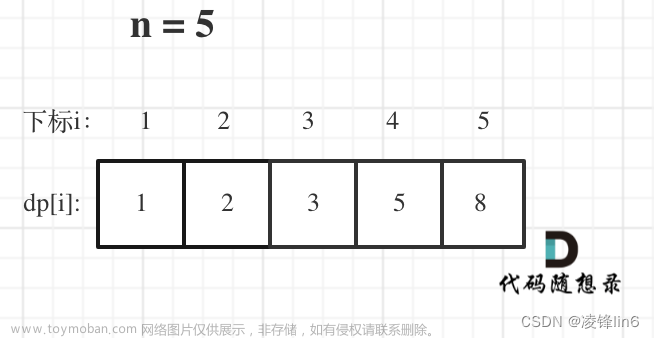
        vector<int>dp(n+1);
        //dp[i]:到达第i个台阶有dp[i]种方法
        dp[1] = 1;
        dp[2] = 2;
        for(int i = 3;i <= n;i++){
            dp[i] = dp[i-1]+dp[i-2];
        }
        return dp[n];
    }
};

到了这里，关于70. 爬楼梯的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：如若内容造成侵权/违法违规/事实不符，请点击违法举报进行投诉反馈，一经查实，立即删除！

分享到：

领支付宝红包赞助服务器费用

代码随想录Leetcode70. 爬楼梯

空间复杂度为O(N)，如果想要优化空间复杂度，则只用三个变量进行状态转移也可以，参考代码随想录 Leetcode509. 斐波那契数-CSDN博客

2024年02月19日
浏览(36)
LeetCode：509. 斐波那契数 && 70. 爬楼梯 && 746. 使用最小花费爬楼梯

斐波那契数（通常用 F(n) 表示）形成的序列称为斐波那契数列。该数列由 0 和 1 开始，后面的每一项数字都是前面两项数字的和。也就是： F(0) = 0，F(1) = 1 F(n) = F(n - 1) + F(n - 2)，其中 n 1 给定 n ，请计算 F(n) 。假设你正在爬楼梯。需要 n 阶你才能到达楼顶。每次你可以爬

2024年02月05日
浏览(38)
leetcode每日一练-第70题-爬楼梯

一、思路动态规划二、解题方法使用一个动态规划数组 dp 来记录到达每个台阶的不同方法数。初始情况下，当台阶数为 1 时，方法数为 1，当台阶数为 2 时，方法数为 2。然后，我们从第 3 阶开始逐步计算每一阶的方法数，方法数等于前一阶和前两阶方法数之和。最终，

2024年02月14日
浏览(40)
LeetCode 70. 爬楼梯 C/C++/Python

欢迎关注博主 Mindtechnist 或加入【Linux C/C++/Python社区】一起探讨和分享Linux C/C++/Python/Shell编程、机器人技术、机器学习、机器视觉、嵌入式AI相关领域的知识和技术。专栏：LeetCode刷题题目描述假设你正在爬楼梯。需要 n 阶你才能到达楼顶。每次你可以爬 1 或 2 个台阶。你有

2024年02月13日
浏览(29)
leetcode 70.爬楼梯+209.长度最小的子数组

70. 爬楼梯 - 力扣（LeetCode）题目：假设你正在爬楼梯。需要 n 阶你才能到达楼顶。每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？示例：输入： n = 3 输出： 3 解释：有三种方法可以爬到楼顶。 1. 1 阶 + 1 阶 + 1 阶 2. 1 阶 + 2 阶 3. 2 阶 +

2024年02月03日
浏览(39)
【LeetCode题目详解】第九章动态规划part01 509. 斐波那契数 70. 爬楼梯 746. 使用最小花费爬楼梯（day38补）

斐波那契数（通常用 F(n) 表示）形成的序列称为斐波那契数列。该数列由 0 和 1 开始，后面的每一项数字都是前面两项数字的和。也就是：给定 n ，请计算 F(n) 。示例 1：示例 2：示例 3：提示： 0 = n = 30 斐波那契数列大家应该非常熟悉不过了，非常适合作为动规第

2024年02月07日
浏览(33)
算法Day38 | 动态规划，509. 斐波那契数， 70. 爬楼梯， 746. 使用最小花费爬楼梯

动态规划是一种解决问题的算法思想。它通常用于优化问题，其中要求找到一个最优解或最大化（最小化）某个目标函数。动态规划的核心思想是将问题分解成更小的子问题，并通过存储子问题的解来避免重复计算。这样，可以通过解决子问题来构建原始问题的解。动态规

2024年02月09日
浏览(44)
算法训练Day45:70. 爬楼梯（进阶） 322. 零钱兑换 279.完全平方数

Category Difficulty Likes Dislikes ContestSlug ProblemIndex Score algorithms Easy (54.04%) 2993 0 - - 0 Tags 记忆 | 数学 | 动态规划 Companies 假设你正在爬楼梯。需要 n 阶你才能到达楼顶。每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？示例 1：示例 2：提示： 1 = n = 45

2024年02月01日
浏览(32)
算法训练第三十八天|动态规划理论基础、509. 斐波那契数、70. 爬楼梯、 746. 使用最小花费爬楼梯

参考：https://programmercarl.com/%E5%8A%A8%E6%80%81%E8%A7%84%E5%88%92%E7%90%86%E8%AE%BA%E5%9F%BA%E7%A1%80.html 动态规划是什么动态规划，英文：Dynamic Programming，简称DP，如果某一问题有很多重叠子问题，使用动态规划是最有效的。所以动态规划中每一个状态一定是由上一个状态推导出来的，这一

2024年02月04日
浏览(31)
算法训练第四十五天|70. 爬楼梯（进阶）、322. 零钱兑换、279.完全平方数

题目链接：70. 爬楼梯（进阶）参考：https://programmercarl.com/0070.%E7%88%AC%E6%A5%BC%E6%A2%AF%E5%AE%8C%E5%85%A8%E8%83%8C%E5%8C%85%E7%89%88%E6%9C%AC.html 假设你正在爬楼梯。需要 n 阶你才能到达楼顶。每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢？注意：给定 n 是一个正整数

2023年04月26日
浏览(50)