北京林业大学数据结构实验二基于栈的算术表达式求值算法-Toy模板网

这篇具有很好参考价值的文章主要介绍了北京林业大学数据结构实验二基于栈的算术表达式求值算法。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

第1关：基于栈的中缀算术表达式求值

参见课本P75 例3.3

#include <iostream>
#include<iomanip>

#define MAXSIZE 100
#define OK 1
#define ERROR 0
#define OVERFLOW -2
typedef int Status;
using namespace std;
typedef struct {//运算符栈
    char *base;
    char *top;
    int stacksize;
} SqStack1;

Status InitStack1(SqStack1 &S) {//运算符栈初始化
    S.base = new char[MAXSIZE];
    if (!S.base) return ERROR;
    S.top = S.base;
    S.stacksize = MAXSIZE;
    return OK;
}

Status Push1(SqStack1 &S, char e) {//运算符栈入栈
    if (S.top - S.base == S.stacksize) return ERROR;
    *S.top = e;
    S.top++;
    return OK;

}

Status Pop1(SqStack1 &S) {//运算符栈出栈
    if (S.top == S.base) return ERROR;
    S.top--;
    return OK;

}

char GetTop1(SqStack1 S) {//运算符栈取栈顶元素

    if (S.top != S.base)
        return *(S.top - 1);
}

typedef struct {//操作数栈
    double *base;
    double *top;
    int stacksize;
} SqStack2;

Status InitStack2(SqStack2 &S) {//操作数栈初始化
    S.base = new double[MAXSIZE];
    if (!S.base) return ERROR;
    S.top = S.base;
    S.stacksize = MAXSIZE;
    return OK;
}

Status Push2(SqStack2 &S, double e) {//操作数栈入栈
    if (S.top - S.base == S.stacksize) return ERROR;
    *S.top = e;
    S.top++;
    return OK;
}

Status Pop2(SqStack2 &S) {//操作数栈出栈
    if (S.top == S.base) return ERROR;
    S.top--;
    return OK;
}

double GetTop2(SqStack2 S) {//操作数栈取栈顶元素
    if (S.top != S.base)
        return *(S.top - 1);
}

double Calculate(double a, char op, double b) {//计算表达式“a op b”的值
    switch (op) {
        case '+':
            return a + b;
            break;
        case '-':
            return a - b;
            break;
        case '*':
            return a * b;
            break;
        case '/':
            return a / b;
            break;
        default:
            return 0;
    }
}

char Precede(char a, char b) {//比较运算符a和b的优先级 没什么好说的枚举就完事了
    if ((a == '(' && b == ')') || (a == '=' && b == '='))return '=';
    else if (((a == '+' || a == '-' || a == '*' || a == '/' || a == ')') &&
              (b == '+' || b == '-' || b == ')' || b == '=')) ||
             ((a == '*' || a == '/' || a == ')') && (b == '*' || b == '/')))
        return '>';
    else if (((a == '(' || a == '=') && b != ')' && b != '=') || ((a == '+' || a == '-') && (b == '*' || b == '/')) ||
             a == '(' || b == '(')
        return '<';
}

bool judge(const char c) {
    if (c == '+' || c == '-' || c == '*' || c == '/' || c == '=' || c == '(' || c == ')') return true;
    return false;
}

double EvaluateExpression(SqStack1 OPTR, SqStack2 OPND, char s[]) {//算术表达式求值的算符优先算法
    //设OPTR和OPND分别为运算符栈和操作数栈
    //表达式求值算法调用Precede函数和Calculate函数
    OPTR.top = OPTR.base;
    OPND.top = OPND.base;
    Push1(OPTR, '=');
    char theta;
    double a = 0, b = 0;
    int i = 0;
    while (s[i] != '=' || GetTop1(OPTR) != '=' && i < MAXSIZE) {
        // 对数字进行解析
        if (!judge(s[i])) { // 解析数字求出数字
            // 整数部分
            double result = 0;
            while (s[i] != '.' && s[i] >= '0' && s[i] <= '9') {
                result = result * 10 + (s[i] - 48);
                ++i;
            }

            // 小数部分
            double result1 = 0;
            double Multiplier = 1.0 / 10;
            if (s[i] == '.') i++;

            while (s[i] >= '0' && s[i] <= '9') {
                result1 += Multiplier * (s[i] - 48);
                Multiplier *= 1.0 / 10;
                i++;
            }

            result += result1;
//            cout << result << endl;
            Push2(OPND, result);
        } else
            switch (Precede(GetTop1(OPTR), s[i])) {
                case '<':
                    Push1(OPTR, s[i]);
                    i++;
                    break;
                case '>':
                    theta = GetTop1(OPTR);
                    Pop1(OPTR);

                    a = GetTop2(OPND);
                    Pop2(OPND);
                    b = GetTop2(OPND);
                    Pop2(OPND);

                    Push2(OPND, Calculate(b, theta, a));
                    break;

                case '=':
                    Pop1(OPTR);
                    i++;
                    break;

            }
    }

    return GetTop2(OPND);
}

第2关: 中缀表达式转化为后缀表达式

#include<iostream>

using namespace std;
#define  MAXSIZE  100
#define OK 1
#define ERROR 0
#define OVERFLOW -2
typedef int Status;
typedef struct {
    char *base;
    char *top;
    int stacksize;
} SqStack;

Status InitStack(SqStack &S) {//初始化栈
    S.base = new char[MAXSIZE];
    if (!S.base) return ERROR;
    S.top = S.base;
    S.stacksize = MAXSIZE;
    return OK;
}

Status Push(SqStack &S, char e) {//入栈
    if (S.top - S.base == S.stacksize) return ERROR;
    *S.top = e;
    S.top++;
    return OK;
}

Status Pop(SqStack &S) {//出栈
    if (S.top == S.base) return ERROR;
    S.top--;
    return OK;
}

char GetTop(SqStack S) {//取栈顶元素
    if (S.top != S.base)
        return *(S.top - 1);
}

char Precede(char a, char b) {//比较运算符a和b的优先级
    if ((a == '(' && b == ')') || (a == '=' && b == '='))return '=';
    else if (((a == '+' || a == '-' || a == '*' || a == '/' || a == ')') &&
              (b == '+' || b == '-' || b == ')' || b == '=')) ||
             ((a == '*' || a == '/' || a == ')') && (b == '*' || b == '/')))
        return '>';
    else if (((a == '(' || a == '=') && b != ')' && b != '=') || ((a == '+' || a == '-') && (b == '*' || b == '/')) ||
             a == '(' || b == '(')
        return '<';
}

bool judge(const char c) {
    if (c == '+' || c == '-' || c == '*' || c == '/' || c == '=' || c == '(' || c == ')') return true;
    return false;
}

void InfixToSuffix(SqStack OPTR, char s[]) {//将中缀表达式转化为后缀表达式并输出
    int i = 0;
    while ((s[i] != '=' || GetTop(OPTR) != '=') && s[i] != '\0') {
    if(!judge(s[i])){
        cout << s[i];
        i++;
    }
    else{
        switch (Precede(GetTop(OPTR),s[i])) {
            case '<':
                Push(OPTR,s[i]);
                i++;
                break;
            case '>':
                if(GetTop(OPTR) != ')' && GetTop(OPTR) != '(')
                cout << GetTop(OPTR);
                Pop(OPTR);
                break;

            case '=':
                if(GetTop(OPTR) != ')' && GetTop(OPTR) != '(')
                cout << GetTop(OPTR);
                Pop(OPTR);
                i++;
                break;
        }
    }
    }
    cout << endl;
}

第3关：基于栈的后缀算术表达式求值

#include <iostream>
#include<iomanip>
#include <string>
#define MAXSIZE 100
#define OK 1
#define ERROR 0
#define OVERFLOW -2
typedef int Status;
using namespace std;
typedef struct {//操作数栈
    double *base;
    double *top;
    int stacksize;
} SqStack;

Status InitStack(SqStack &S) {//操作数栈初始化
    S.base = new double[MAXSIZE];
    if (!S.base) return ERROR;
    S.top = S.base;
    S.stacksize = MAXSIZE;
    return OK;
}

Status Push(SqStack &S, double e) {//操作数栈入栈
    if (S.top - S.base == MAXSIZE) return ERROR;
    *S.top = e;
    S.top ++;
    return OK;
}

Status Pop(SqStack &S) {//操作数栈出栈
    if (S.top == S.base) return ERROR;
    S.top--;
    return OK;
}

double GetTop(SqStack S) {//操作数栈取栈顶元素
    if (S.top != S.base) return *(S.top - 1);
}

double Calculate(double a, char op, double b) {//计算表达式“a op b”的值
    switch (op) {
        case '+':
            return a + b;
            break;
        case '-':
            return a - b;
            break;
        case '*':
            return a * b;
            break;
        case '/':
            return a / b;
        default:
            return 0;
    }
}
bool judge(char c){
    if(c == '+' || c == '-' || c == '*' || c == '/' || c == '='  )
        return true;
    return false;
}
double EvaluateExpression(SqStack OPND, char s[]) {//后缀算术表达式求值
    //设OPND为操作数栈
    //表达式求值算法调用Calculate函数
    char theta;
    double a, b;
    int i = 0;
    while (s[i] != '='){
        if(s[i] == ' ') {
            i++;
            continue;
        }
        if(!judge(s[i])){
            double num = s[i] - 48;
            Push(OPND,num);
            i++;
            continue;
        }
        else{

            b = GetTop(OPND);
            Pop(OPND);
            a = GetTop(OPND);
            Pop(OPND);
            Push(OPND, Calculate(a,s[i],b));
            i++;
        }
        }
    return GetTop(OPND);
}

第4关：入栈和出栈的基本操作

#include<iostream>

using namespace std;
#define  MAXSIZE  100
#define OK 1
#define ERROR 0
#define OVERFLOW -2
typedef int Status;
typedef struct {
    int *base;
    int *top;
    int stacksize;
} SqStack;

Status InitSqStack(SqStack &S) {//栈的初始化
    S.base = new int [MAXSIZE];
    if (!S.base) return ERROR;
    S.top = S.base;
    S.stacksize = MAXSIZE;
    return OK;
}

Status Push(SqStack &S, int e) {//入栈
    if (S.top - S.base == S.stacksize) return ERROR;
    *S.top = e;
    S.top++;
    return OK;
}

Status Pop(SqStack &S) {//出栈
    if (S.top == S.base) return ERROR;
    S.top--;
    return OK;
}

Status GetTop(SqStack S) {//取栈顶元素
    if (S.top != S.base)
        return *(S.top - 1);
    else return 0;
}
//本关任务：输入一个整数序列a1,a2,a3...,an。当ai不等于-1时将ai进栈；当ai=-1时，输出栈顶元素并将其出栈。
void InOutS(SqStack &S, int a[], int n) {//入栈和出栈的基本操作
    for (int i = 0; i < n; ++i) {
        if(a[i] != -1){
            Push(S,a[i]);
        }
        else{
            if(GetTop(S)){
                cout << GetTop(S) << endl;
                Pop(S);
            }
            else {
                cout << "POP ERROR" << endl;
                break;
        }
    }
}
}

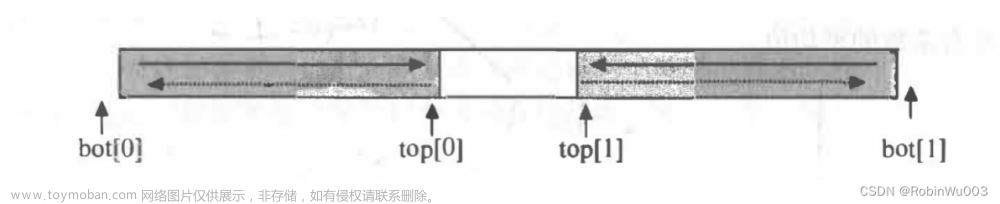
第5关：双栈的基本操作

基于栈的中缀算术表达式求值,算法,数据结构,c++ 文章来源地址https://www.toymoban.com/news/detail-736356.html

#include<iostream>

using namespace std;
typedef int Status;
typedef struct {
    int top[2], bot[2];//栈顶和栈底指针
    int *V;//栈数组
    int m;//栈最大可容纳元素个数
} DblStack;

void InitDblStack(DblStack &S, int m) {//初始化一个大小为m的双向栈
    S.V = new int[m];
    if(!S.V) return;
    S.bot[0] = S.top[0] = -1;
    S.bot[1] = S.top[1] = m;
    return;
}

Status IsEmpty(DblStack S, int i) {//判断指定的i号栈是否为空，空返回1，否则返回0
    if (S.top[i] == S.bot[i]) return 1;
    return 0;
}

Status IsFull(DblStack S) {//判断栈是否满，满则返回1，否则返回0
    if (S.top[0] + 1 == S.top[1])
        return 1;
    return 0;
}

void Push(DblStack &S, int i) {//向指定的i号栈中插入元素x，先移动指针再入栈
    int x;
    cin >> x;
    if (IsFull(S)) return;
    if (i == 0) {
        S.V[++S.top[0]] = x;
    } else {
        S.V[--S.top[1]] = x;
    }

}

void Pop(DblStack &S, int i) {//删除指定的i号栈的栈顶元素，先出栈再移动指针
    if (S.top[i] == S.bot[i]) {
        return;
    }

    if (i == 0) {
        cout << S.V[S.top[0]--] << ' ';
    } else if (i == 1) {
        cout << S.V[S.top[1]++] << ' ';
    }
    return;
}

第6关: 基于栈的回文字符序列判断

#include <iostream>

#define MAXSIZE 100
#define OK 1
#define ERROR 0
#define OVERFLOW -2
typedef int Status;
using namespace std;
typedef struct {
    char *base;
    char *top;
    int stacksize;
} SqStack;

Status InitStack(SqStack &S) {//栈初始化
    S.base = new char[MAXSIZE];
    if (!S.base) return ERROR;
    S.top = S.base;
    S.stacksize = MAXSIZE;
    return OK;
}

Status Push(SqStack &S, char e) {//入栈
    if (S.top - S.base == S.stacksize) return ERROR;
    *S.top = e;
    S.top++;
    return OK;
}

Status Pop(SqStack &S) {//出栈返回栈顶元素
    if(S.top == S.base) return ERROR;
    S.top--;
}
char  Get(SqStack &S){
    if(S.top == S.base) return 0;
    return *(S.top - 1);
}
Status IsPalindrome(SqStack &S, char *t) {//判断栈的回文字符序列，不等则返回零, 相等则返回1
    int i = 0;
    while (t[i] != '\0'){
//        cout << t[i] << endl;
        Push(S,t[i]);
        i++;
    }
    i--;
    for (int j = 0; j < i; ++j) {
        char e = Get(S);
        if(t[j] != e) return 0;
        Pop(S);
    }
    return 1;

}

第7关：基于栈的可操作判断

#include <iostream>

#define MAXSIZE 100
#define OK 1
#define ERROR 0
#define OVERFLOW -2
typedef int Status;
using namespace std;
typedef struct {
    char *base;
    char *top;
    int stacksize;
} SqStack;

Status InitStack(SqStack &S) {//初始化栈
    S.base = new char[MAXSIZE];
    if (!S.base) return ERROR;
    S.top = S.base;
    S.stacksize = MAXSIZE;
    return OK;
}

Status Push(SqStack &S) {//入栈
    if (S.top - S.base == S.stacksize) return ERROR;
    S.top++;
    return OK;
}

Status Pop(SqStack &S) {//出栈
    S.top--;
}

Status IsEmpty(SqStack S) {//判断栈是否为空，空返回1，否则返回0
    if(S.top == S.base) return 1;
    return 0;
}

bool Judge(char a[], SqStack &S) {//栈的可操作判断
int pos = 0;
    while (a[pos] != '\0'){
        if(a[pos] == 'I') Push(S);
        else {
            if(IsEmpty(S)) return 0;
            else Pop(S);
        }
        pos++;
    }
    return IsEmpty(S);
}

第8关：Ackermann函数的递归求值

#include<iostream>

using namespace std;

int Ack(int m, int n) {//Ackermann函数的递归求值
    if (m == 0) return n + 1;
    if (m > 0 && n == 0) return Ack(m - 1, 1);
    return Ack(m - 1, Ack(m, n - 1));
}

第9关：Ackermann函数的非递归求值

#include<iostream>

using namespace std;
#define MAXSIZE 100

int Ack(int m, int n) {//Ackermann函数的非递归求值
    int arrary[m + 1][MAXSIZE ];
    for (int j = 0; j < MAXSIZE; j++)
        arrary[0][j] = j + 1;
    for (int i = 1; i <= m; i++) {
        arrary[i][0] = arrary[i - 1][1];
        for (int j = 1; j < MAXSIZE; j++)
            arrary[i][j] = arrary[i - 1][arrary[i][j - 1]];
    }
    return (arrary[m][n]);
}

第10关：递归求解单链表中的最大值

#include <iostream>
#include "algorithm"
using namespace std;
typedef struct LNode {
    int data;
    struct LNode *next;
} LNode, *LinkList;

void CreateList_R(LinkList &L, int n) {//后插法创建单链表
   L = new LNode();
   LinkList pre = L;
    for (int i = 0; i < n; ++i) {
        LinkList cur = new LNode();
        cin >> cur->data;
        pre->next = cur;
        pre = pre->next;
    }
}

int GetMax(LinkList L) {//递归求解单链表中的最大值
    if( L == nullptr) return INT32_MIN;
    return max(L->data, GetMax(L->next));
}

第11关：递归求解单链表中的结点个数

#include <iostream>

using namespace std;
typedef struct LNode {
    int data;
    struct LNode *next;
} LNode, *LinkList;

void CreateList_R(LinkList &L, int n) {//后插法创建单链表
    L = new LNode();
    LinkList pre = L;
    for (int i = 0; i < n; ++i) {
        LinkList cur = new LNode();
        cin >> cur->data;
        pre->next = cur;
        pre = pre->next;
    }
}

int GetLength(LinkList L) {//递归求解单链表中的结点个数
    if(L == nullptr)return 0;
    return 1 + GetLength(L->next);
}

第12关：递归求解单链表中的平均值

#include <iostream>

using namespace std;
typedef struct LNode {
    int data;
    struct LNode *next;
} LNode, *LinkList;

void CreateList_R(LinkList &L, int n) {//后插法创建单链表
    L = new LNode();
    LinkList pre = L;
    for (int i = 0; i < n; ++i) {
        LinkList cur = new LNode();
        cin >> cur->data;
        pre->next = cur;
        pre = pre->next;
    }
}

double GetAverage(LinkList L, int n) {//递归求解单链表中的平均值
    if (L == nullptr) return 0;
    if(n == 1) return L->data;
    return (L->data + (n - 1) * GetAverage(L->next, n - 1)) / n;
}

第13关：基于循环链表的队列的基本操作

#include<iostream>

using namespace std;
typedef int Status;
typedef struct QNode {//队列的链式存储结构
    int data;
    struct QNode *next;
} QNode, *QueuePtr;
typedef struct {
    QueuePtr rear;    //只设一个队尾指针
} LinkQueue;

Status EmptyQueue(LinkQueue Q) {//判断队列是否为空，空返回1，否则返回0
//队列只有一个头结点，即当头结点的指针域指向自己时，队列为空
    if (Q.rear->next == Q.rear) return 1;
    return 0;
}

void EnQueue(LinkQueue &Q, int e) {//入队，插入元素e为Q的新的队尾元素
    QueuePtr queuePtr = new QNode();
    queuePtr->data = e;
    queuePtr->next = Q.rear->next;
    Q.rear->next = queuePtr;
    Q.rear = Q.rear->next;
}

void DeQueue(LinkQueue &Q) {//出队，输出Q的队头元素值，后将其删除
    QueuePtr q = Q.rear->next->next;
    cout << q->data << ' ';
    Q.rear->next->next = q->next;
    if (q == Q.rear) {
        Q.rear = Q.rear->next;
    }

}

第14关：附加判定标志的循环队列的基本操作

#include<iostream>

using namespace std;
#define MAXSIZE 100
#define OK 0
#define OVERFLOW -1
#define ERROR -2
typedef int Status;
typedef struct {
    int *base;
    int front, rear, tag;
} SqQueue;

Status InitQueue(SqQueue &Q) {//构造一个空队列Q
    Q.base = new int[MAXSIZE];
    if (!Q.base) return ERROR;
    Q.front = Q.rear = 0;
    return OK;
}

Status EnQueue(SqQueue &Q, int e) {//插入元素e为Q的新的队尾元素
    if ((Q.rear + 1) % MAXSIZE == Q.front) return ERROR;
    Q.base[Q.rear] = e;
    Q.rear = (Q.rear + 1) % MAXSIZE;
    return OK;
}

Status DeQueue(SqQueue &Q) {//删除Q的队头元素，用e返回其值
    if (Q.front == Q.rear) return ERROR;
    auto e = Q.base[Q.front];
    Q.front = (Q.front + 1) % MAXSIZE;
    return e;
}

第15关：基于两端操作的循环队列的实现

#include<iostream>

using namespace std;
#define MAXSIZE 100
#define OK 0
#define OVERFLOW -1
#define ERROR -2
typedef int Status;
typedef struct {
    int *base;
    int front, rear, tag;
} SqQueue;

Status InitQueue(SqQueue &Q) {//构造一个空队列Q
    Q.base = new int[MAXSIZE];
    if (!Q.base) return ERROR;
    Q.front = Q.rear = 0;
    return OK;
}

Status EnQueue(SqQueue &Q, int e) {//插入元素e为Q的新的队尾元素
    if ((Q.rear + 1) % MAXSIZE == Q.front) return ERROR;
    Q.base[Q.rear] = e;
    Q.rear = (Q.rear + 1) % MAXSIZE;
    return OK;
}

Status DeQueue(SqQueue &Q) {//删除Q的队头元素，用e返回其值
    if (Q.front == Q.rear) return ERROR;
    auto e = Q.base[Q.front];
    Q.front = (Q.front + 1) % MAXSIZE;
    return e;
}

到了这里，关于北京林业大学数据结构实验二基于栈的算术表达式求值算法的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！