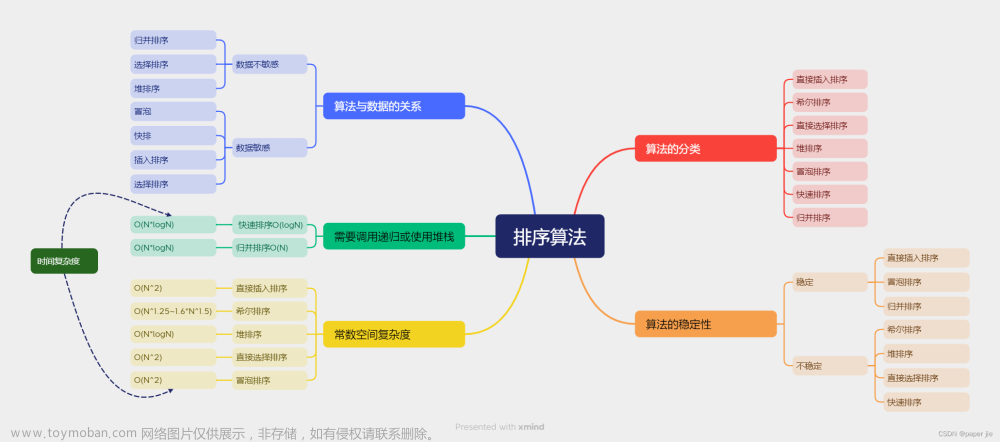
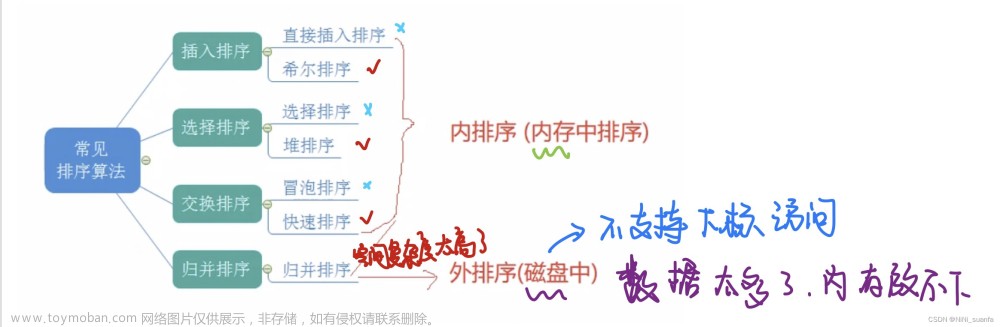
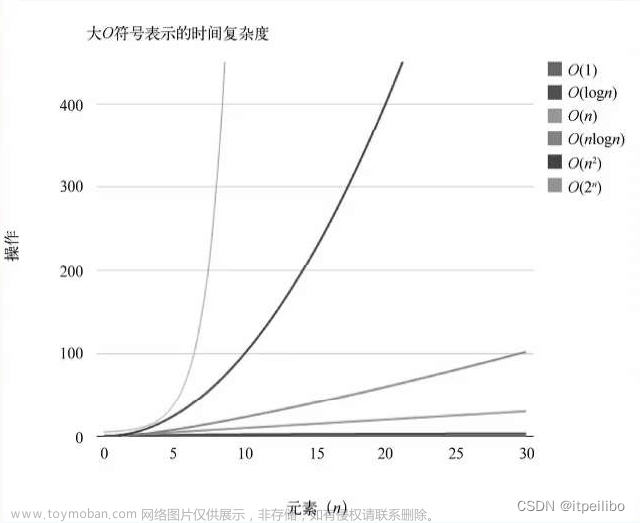
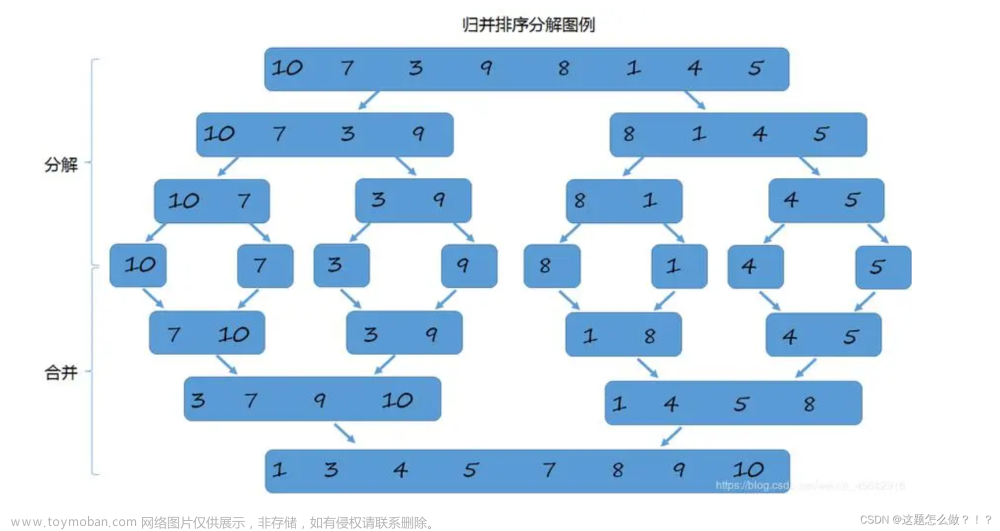
排序
-
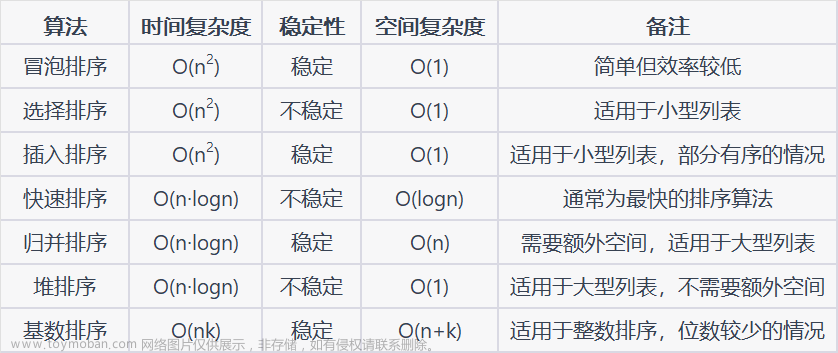
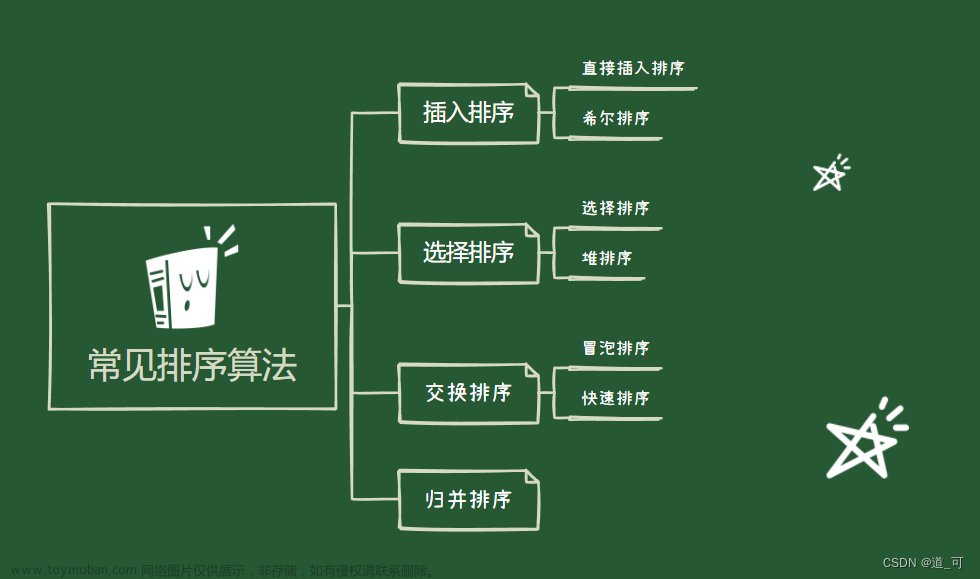
冒泡排序
思想:两数比较,将最大或者最小的元素,放到最后
int i , j , temp //定义 外层循环变量 i 内层循环变量 j 临时变量 temp
for( i = 0 ; i< len - 1 ; i++){ //外层 控制 比较多少趟
for( j = 0 ; j < len - i -1 ; j++){ //内层 控制 元素 一趟比较的次数
if( arr[j] > att[j+1]){ //从小到大排序
temp = arr[j];
arr[j] = arr[j+1];
arr[j+1] = temp;
}
}
}
- 例题
题目:定义一个数组,长度 10 , 子函数 键盘输入元素,子函数遍历数组,子函数进行冒泡排序,最终将排序好的元素,打印到文件中
-
顺序表下的 冒泡排序
typedef int keyType //关键字
typedef struct{
ketType key;
}RecType; //单个结点的数据类型
typedef struct{
RecType r[10000];
int len; //顺序表长度
}SqList; //顺序表的数据类型
int i , j , temp;
SqList *q;
for(i = 0; i < q->len-1 ; i++){
for(j = 0 ; j < q->len-i-1 ; j++){
if(q->r[j].key > q->r[j + 1].key){
temp = q->r[j].key;
q->r[j].key = q->r[j + 1].key;
q->r[j + 1].key = temp;
}
}
}
注意:冒泡排序 稳定,最多执行n(n-1)/2次
选择排序
选择排序,找最大或者最小的元素 往前放,分成 已排序和待排序序列
void selectSort(int arr[] , int len){
int i , j , temp , min;
for(i = 0 ;i < len ; i++){
min = i; //min 标记 未排序第一个元素的位置
for(j = i + 1 ; j < len ; j++){ //找比 min 位置还小的元素
if(arr[j] < arr[min]){
min = j;
}
}
if(min != i){
temp = arr[min];
arr[min] = arr[i];
arr[i] = temp;
}
}
}
题目:定义一个数组,键盘输入10个数据,利用选择冒泡排序从小到大输出在控制台上,并写入文件,另子函数读取文件,利用选择排序从大到小输出在控制台上。
选择排序不稳定,平均比较次数n(n-1)/2
直接插入排序
从后向前进行 查找 确定位置,并插入元素
void insertSort(int arr[] , int len){
int i , j , temp;
for(i = 1; i < len; i++){ //从 1 开始,0 位置当成有序
temp = arr[i]; //temp 记录未排序第一个
for(j = i - 1; j >= 0 && arr[j] > temp; j--){
arr[j+1] = arr[j]; //元素后移,腾位置给插入元素
}
arr[j+1] = temp; //插入 比较的 后一位
}
}
题目:选择功能,1、选择排序(从小到大) 2、直接插入排序(从大到小) 3、冒泡排序(从小到大)
选择分支结构,定义数组,键盘输入值,实现以上 三个子函数的功能
直接插入排序,是在有序基础上,速度最快且稳定的排序方法。
希尔排序
按照 步长 进行分组,然后每一组的 第 几个 元素 进行排序
增量 及 步长
//dk 是增量 步长
void shellInsert(int arr[] , int len ,int dk){
int i , j , temp; //i 循环变量 j 前边组的位置 temp 临时变量
for(i = dk; i < len; i++){
//判断每组的 第几个元素大小
if(arr[i] < arr[i-dk]){ //后编组 小于 前边组
temp = arr[i];
j = i - dk;
for(; j >= 0 && temp <arr[j]; j = j - dk){
//前边的值 给到 后边
arr[j + dk] = arr[j];
}
arr[j + dk] = temp;
}
}
}
希尔排序是 不稳定的
快速排序
基准值,i 从前向后找,比基准值大的元素 j 从后向前找,找比基准值小的元素,最后,结束条件 i = j 此时将 基准值放到这个位置
int getPivot(int arr[] , int low , int high){
int pivot = arr[low];
while(low < high){ //i < j 的时候
// j 从后向前找,比基准值 小的元素
while(low < high && arr[high] >= pivot){
high--;
}
//找到了 比基准值小的元素 将元素 给到 i 位置
arr[low] = arr[high];
//i 从前向后找,比基准值 大的元素
while(low < high && arr[low] <= pivot){
low++;
}
//找到了 比基准值大的元素 将元素 给到 j 位置
arr[high] = arr[low];
}
//结束条件 i = j 找到了基准值的位置
arr[low] = pivot;
//返回基准值
return low;
}
void quickSort(int arr[] , int low ,int high){
if(low < high){
//基准值位置的变量
int pivot = getPivot(arr , low , high);
//递归 对 基准值位置 左边进行 快速排序
quickSort(arr , low , pivot-1);
//递归 对 基准值位置 右边进行 快速排序
quickSort(arr , pivot+1 , high);
}
}
查找
- 顺序查找
遍历数组,拿元素依次比较,相同返回 下标,找不到,返回 -1
//arr 数组 len 数组长度 value 要查找的值
void linearSearch(int arr[] , int len , int value){
int i;
for(i = 0 ; i < len ; i++){
if(arr[i] == value){
return i;
}
}
return -1; //找不到
}
- 二分查找(非递归)
//arr 数组,low 左边值,high 右边值,key 要查找的关键字
int binarySearch(int arr[] , int low , int high , int key){
int mid; //中间值
while(low <= high){
mid = (low +high)/2; //找中间位置
if(key == arr[mid]){
return mid; //返回下标
}else if(key > arr[mid]){
low = mid + 1;
}else{
high = mid - 1;
}
}
//没有找到关键字
return -1;
}
- 二分查找(递归)
int binarySearch(int arr[] , int low , int high , int key){
int mid; //中间下标
if(low <= high){
mid = (low + high)/2;
if(key == arr[mid]){
return mid; //递归出口
}else if(key > arr[mid]){
return binarySearch(arr , mid+1 , high , key);
}else{
return binarySearch(arr , low , mid-1 , key);
}
}
return -1;
}
题目:主函数定义 数组 长度为5,键盘输入 5 个元素,子函数一,实现二分查找递归式子,子函数儿,实现二分查找,非递归方式。并输出
线性表
1、顺序表(数组)
//顺序表 一般 占用一片连续的存储空间
2、链表
//链表,结点在内存中随机分配,指针链接起来即可
| 数组 | 链表 | |
|---|---|---|
| 查询 | 快 | 慢 |
| 增删 | 慢 | 快 |
| 索引,移动大量元素 | 只有指针,不需要移动元素 |
遇到数组是,注意:下标从0开始还是从1开始
数组名 是 首元素地址,也是指针
bit 位 0100 0110
byte 字节
1 byte = 8 bit
int arr[] = {1 , 2 , 3 , 4 ,5};
int *p = arr;
//数组的首元素地址
arr == &arr[0] == p
顺序表(数组)
- 输入元素
void input(int arr[] , int len){
//循环变量
int i;
int *p = arr;
for(i = 0;i < len; i++){
printf("请输入%d个元素",i+1);
scanf("%d",&arr[i]);
//scanf("%d",arr + i);
//scanf("%d",p + i);
}
}
- 输出元素(遍历数组)
void output(int arr[] , int len){
//定义循环变量
int i;
int *p = arr;
for(i = 0 ; i < len ;i++){
printf("%d ",arr[i]);
// printf("%d ",*(arr + i));
// printf("%d ",*(p + i));
}
}
- 查询元素
//根据元素的值 去找 下标
int searchvalue(int arr[] , int len ,int value){
int i;
for(i = 0;i < len; i++){
if(value == arr[i]){
return i;
}
}
return -1;
}
//根据下标 查找元素
int searchkey(int arr[] , int len ,int key){
//判断 位置 是否在数组范围之内
if(key < 0 || key > len -1){
printf("位置不对!");
return; //exit(0) j结束程序
}
printf("查找的元素是:%d\n",arr[key]);
}
- 动态生成 数组
int *getArray(int num){ //返回一个指针变量
int i,*p; //p 指向 动态数组首地址
p = (int *)malloc(sizeof(int)*num);
if(!p){
printf("空间申请失败!");
return;
}
return p;
}
- 修改元素
//根据元素值修改
void updateValue(int arr[] , int len){
//修改前 修改后
int firstValue , lastValue , i;
printf("请输入您要修改的元素:\n");
scanf("%d",&firstValue);
printf("请输入您要修改后的元素:\n");
scanf("%d",&lastValue);
for(i = 0; i < len; i++){
if(arr[i] == firstValue){
arr[i] = lastValue;
}
}
}
//根据位置修改
void updateKey(int arr[] , int len){
int key , value;
printf("请输入你要修改的位置:\n");
scanf("%d",&key);
printf("请输入你要修改后的值:\n");
scanf("%d",&value);
if(key < 0 || key > len - 1 ){
printf("位置不对!");
return;
}
arr[key] = value;
}
- 插入元素
void insert(int arr[] , int *len , int index , int value){
int i,temp;
if(index < 0 || index > *len -1 ){
return;
}
//元素后移
for(i = *len - 1; i >= index; i--){
arr[i+1] = arr[i];
}
//插入元素
arr[index] = value;
//长度变化
(*len)++;
}
-
删除元素
void delete(int arr[] , int *len , int index){ int i; if(index < 0 || index > *len - 1){ return; } //元素前移 for(i=index; i<len-1; i++){ arr[i] = arr[i+1]; } //元素删除 长度减少 (*len)--; } -
字符数组
//1、大括号初始化字符数组时,需要预留一个空间 做 结束标志 \0,否则乱码
char a[5] = {'a' , 'b' , 'c' , 'd' , 'c'} //乱码
//2、双引号初始化时,自带结束标志
char str[] = "hello";
strlen 求字符串长度时,不带\0
sizeof 求字符串长度时,带\0
- 字符数组两种 键盘输入方式
1、gets(字符串);
2、scanf("%s",字符串);
//可以校验 是否越界,stdin 是标准输入流(键盘输入)
fgets(a , sizeof(a) , stdin);
链表
- 结点
typedef struct Node{
int data; //数据域
struct Node *next //指针域(存放下一个结点的位置)
}Node;
- 结点类型
1、头结点 //只有指针域,数据域不存放数据,一般用 head 表示
2、首元结点 //第一个存放 数据的 结点
有头结点:方便使用头插法 插入元素
- 链表的初始化(只生成头结点)
typedef struct Node{
int data; //数据域
struct Node *next; //指针域
}Node,*LinkeList;
//Node struct Node 的别名 LinkList struct Node *
//int int *
LinkList create(){
//动态申请空间 (head指针指向这个空间)
LinkList head = (Node *)malloc(sizeof(Node));
//判断空间是否开辟成功
if(!head){
peinrf("空间开辟失败!");
return 0;
}
//头结点,指针域赋值为 NULL
head->next = NULL;
//返回头结点 指针
return head;
}
- 链表长度获取
//实际传的是 头结点地址,但是代表的是一个 链表
int getsize(LinKist head){
//头结点 为 空
if(head == NULL){
return NULL;
}
//p 指向首元结点
Node *p = head->next;
//LinkList q = head->next;
//计数器
int count = 0;
while(p != NULL){
count ++;
p = p->next; //指针后移
}
//返回链表长度
return count;
}
- 链表的遍历(数据域)
void foreach(LinkList head){
if(head == NULL){
return;
}
LinkList p = head->next;
while(p != NULL){
printf("%d ",p->data);
p = p->next; //指针后移
}
}
- 链表的清空
void clear(LinkList head){
if(!head){
return;
}
Node *p = head->next;
while(p != NULL){
//q 存放的是 p 下一个结点地址
LinkList q = p->next;
//释放 p
free(p);
p = q;
}
head->next = NULL;
}
- 链表的销毁
void destroy(LinkList head){
if(head == NULL){
return;
}
clear(head);
free(head);
head = NULL; //指针变量设置为 空
}
- 链表的插入(尾插法)
void insert(LinkList head){
if(!head){
return;
}
int num,i;
printf("请输入你要插入的结点数量:\n");
scanf("%d",&num);
Node *q = head;
for(i = 0 ;i < num ;i++){
LinkList p = (Node *)malloc(sizeof(Node));
printf("请输入数据域的值:");
scanf("%d",&p->data);
q->next = p;
q = q->next;
}
q->next = NULL;
}
尾插法生成 链表
- 链表的插入(头插法)
void insert(LinkList head){
if(head == NULL){
return;
}
int num,i;
printf("请输入你要插入的结点数量:\n");
scanf("%d",&num);
for(i = 0;i < num; i++){
Node * p = (Node *)malloc(sizeof(Node));
printf("请输入数据域的值:");
scanf("%d",&p->data);
p->next = NULL;
//头插法
p->next = head->next;
head->next = p;
}
}
头插法,经常用头指针进行元素的插入
- 链表的删除
//根据元素的值去删除结点
void delete(LinkList head , int value){
if(head == NULL){
return;
}
Node *p = head; //p 指针指向头结点
Node *q;
while(p->next != NULL){
if(p->next->data == value){
q = p->next;
p->next = q->next;
free(q);
}else{
p = p->next;
}
}
}
删除一个结点,必须知道这个结点 的 直接前驱
栈(stack)
- 栈的特点:先进后出 后进先出
1、栈分成了 栈顶 和 栈底 (在栈顶进行元素的插入和删除)
2、入栈 (push) 出栈 (pop)
- 栈的顺序存储 (使用 数组)
数组的首地址做栈顶还是栈底比较好?
答:做栈底 比较好,因为 栈顶要进行元素的插入和删除操作,所以数组尾部更适合比较频繁插入和删除
- 栈的 结构体
typedef struct Stack{
int data[MAX]; //数据域
int size; //栈的大小(栈中元素个数)
}Stack , *SeqStack;
- 栈的初始化
SeqStack create(){
//创建栈,相当于动态开辟一个数组出来
SeqStack p = (Stack *)malloc(sizeof(Stack));
if(p == NULL){
return NULL;
}
//初始化 栈的大小
p->size = 0;
//初始化 栈中的元素
for(int i = 0; i < MAX; i++){
p->data[i] = 0;
}
return p;
}
- 入栈
void push(SeqStack stack , int data){
if(stack == NULL){
return;
}
//入栈 需要判断 栈是否已满
if(stack->size == MAX){
printf("栈已满!\n");
return;
}
//stack->size 栈的大小就是 我们插入元素的下一个位置
stack->data[stack->size] = data;
//改变栈的大小
stack->size++;
}
入栈 需要注意 栈是 不存在 栈是否已满
- 出栈
void pop(SeqStack stack){
if(stack == NULL){
return;
}
if(stack->size == 0){
printf("栈已空!\n");
return;
}
//删除一个元素
stack->data[stack->size - 1] = 0;
//改变栈的大小
stack->size --;
}
出栈 需要注意 栈是否 不存在,和 栈是否已空
- 遍历栈中元素
void foreachSack(SeqStack stack){
if(stack == NULL){
return;
}
for(int i = 0; i < stack->size; i++){
printf("%d ",stack->data[i]);
}
}
栈的链式存储(链表)
链表的头结点端做栈顶还是栈底?
答:栈顶 因为 链表的头结点端 可以 更方便的进行元素的 插入 (头插法) 和 删除 (头结点做直接前驱)
- 栈链式存储 结构体
//结点结构体
typedef struct Node{
int data;
struct Node *next;
}Node;
//栈的结构体
typedef struct Stack{
struct Node header; //头结点
int size; //栈的大小及元素个数
}Stack , *LinkList;
- 初始化栈
LinkStack init_LinkStack(){
//myStack 是指针 指向我们申请的空间
LinkStack myStack = (Stack *)malloc(sizeof(Stack));
if(myStack == NULL){
return NULL;
}
//初始化长度 为 0
myStack->size = 0;
//相当于 初始化链表的头结点 指针域
myStack->header.next = NULL;
}
什么时候使用-> 什么时候使用 . ?
-> 在指针的时候
. 在变量名的时候
- 注意事项
struct Node * list list->data list->next
struct Node a; a.data a.next
- 入栈
void push(LinkStack srack , int data){
if(stack == NULL){
return;
}
//创建一个结点
Node * p = (Node *)malloc(sizeof(Node));
//给结点数据域 赋值
p->data = data;
//头插法 线连后边
p->next = stack->header.next;
stack->header.next = p;
//改变栈中元素的个数
stack->size++;
}
- 出栈
void pop(LinkStack stack){
if(stack == NULL){
return;
}
if(stack->size == 0){
printf("栈中无元素!");
return;
}
//定义一个结点类型指针 用作 删除 结点
Node *p = stack->header.next;
//头结点 连接 到 删除结点后边
stack->header.next = p->next;
//释放结点
free(p);
//更新栈大小
stack->size --;
}
队列
- 队列:先进先出 后进后出
1、只允许从 一端添加元素 从另一端删除元素
2、对头 出元素 队尾 进元素
3、push pop
- 队列的顺序存储
数组的首地址 做队头好,还是队尾好
答:都一样,做对头 和 队尾差别不大,因为 都需要移动大量元素
- 队列的结构体
typedef struct Queue{
int data[MAX]; //顺序存储 数组模拟的队列
int size; //队列的大小(队列中元素个数)
}Queue , *SeQueue;
- 队列的初始化(数组头做对头,数组尾做队尾)
SeQueue init(){
//申请队列空间,即数组空间
SeQueue p = (Queue *)malloc(sizeof(Queue));
if(p == NULL){
return NULL;
}
//初始化 队列大小
p->zieof = 0;
int i;
for(i = 0; i < MAX; i++){
p->data[i] = 0;
}
return p;
}
- 队列的入队
void push(SeQueue p , int value){
if(p == NULL){ //队列不存在
return;
}
if(p->size == MAX){
printf("队列元素已满!\n");
return;
}
//进队
p->data[p->size] = value;
//改变队列元素个数
p->size ++;
}
- 出队
void push(SeQueue p){
if(p == NULL){ //队列不存在
return;
}
if(p->size == 0){
printf("队列元素已空!\n");
return;
}
//出队 删除数组首元素
int i;
for(i = 0; i < p->size-1 ; i++){
p->data[i] = p->data[i+1];
}
//改变队列元素个数
p->size --;
}
要记得,看到循环里边有 i + 1 的时候,要改变 最终值
- 队列的链式存储
链表的 头结点端 做对头 还是 队尾?
答:做对头好,因为 头结点端进行删除方便,尾端 插入元素方便(尾插法)
- 队列链式结构体
struct Node
{
int data; //数据域
struct Node* next; //指针域
};
//队列的结构体
typedef struct LQueue
{
struct Node header; //头结点
int size; //队列大小
struct Node* pTail; //尾结点指针
}LQueue, *LinkQueue;
- 循环队列
//队满
front = (rear + 1)%n; //front 头,rear 尾
//队空
front = rear; //头指针 指向 尾指针 为空
栈的应用
- 前 中 后 缀表达式如何计算?
首先运算优先级最高的,然后 将 运算符 放两个整体 之前 就是 前缀,放两个整体之后,就是 后缀!
串
-
零个或者多个任意字符组成的有限序列是我们的字符串
-
串 是 内容受限的线性表
-
子串:一个串中 任意一个连续字符组成的子序列(含空串)
"*jkj12k0" //它的字串有那些
// 单个字符 6
// 俩个字符 7
// 三个字符 6
// 四个字符 5
// 五个字符 4
// 六个字符 3
// 七个字符 2
// 八个字符 1
// 空串 1
35
- 真子串(不包含自身的子串)
- 主串:包含子串的串,称之为 主串
- 字符位置:字符在数组中的位置
- 子串位置:子串第一个字符 在 主串中的位置
- 空格串:一个空格或者多个空格组成的串,称之为空格串
- 空串:零个没有任意字符的串就是我们的空串
" " //空格串
"" //空串
- 串相等:当两个串长度相等,并且每个位置对应字符完全一样的时候,两个串才相等。
串的基本操作
1. 赋值 StrAssign(s,t) 将串t的值赋值给串s
2. 求串长 StrLength(s) 返回字符串s的长度
3. 串比较 StrCompare(s,t) 比较两个串,返回-1、0和1,分别代表s<t、s=t和s>t
4. 连接 Concat(s,t) 将串t连接在串s的尾部,形成新的字符串
5. 求子串 SubString(s,start,len) 返回串s从start开始、长度为len的字符序列
6. 串拷贝 StrCopy(t,s) 将串s拷贝到串t上
7. 串判空 StrEmpty(s) 判断串s是否为空串
8. 清空串ClearString(s) 清空字符串s
9. 子串位置 Index(S,T,pos) 字符串S中返回T所出现的位置
10. 串替换 Replace(S,T) 串S替换为T
- 串的顺序存储
- 结构体
typedef struct SString{
char ch[MAX + 1]; //字符数组空间
int lingth; //串的长度
};
- BF算法
//str 是主串 subStr是模式匹配串
int BF(char str[] , char subStr[]){
int i , j; //定义 i 主串下标 j 模式串下标
i = 0;
j = 0;
while(i < strlen(str) && j < strlen(subStr)){
//如果对应位置相等,则下标后移比较下一个元素
if(str[i] == subStr[j]){
i++;`标进行回溯
j = 0; //子串下标回溯
}
}
if(j == strlen(subStr)){ //子串下标 和 子串长度相等
//返回 子串位置
return i - strlen(subStr) + 1;
}
return -1; //没有找到子串下标
}
矩阵
- 把矩阵当作 二维数组,只不过下标都是从 1 开始
- 二维数组 以行为主序存储,二维数组 以列为主序存储
以行存储,先去计算前 i - 1 行有多少元素
以列存储,先去计算前 j - 1 列有多少元素
前提:数组下标 从 1 开始
-
对称矩阵:以主对角线为对称轴,各元素对应相等的矩阵
-
对角矩阵:除主对角线以外,全是 0 的矩阵
-
稀疏矩阵:非零元素个数,远远少于 零元素个数,且零元素分布没有规律
-
三元组(行,列,值)
(4 , 5 , 8) //第四行,第五列,值为 8
树
- 树是非线性结构
- 根结点:没有父结点的结点,称之为 根结点
- 叶子结点:没有子节点的结点
- 结点的层次:有几层
- 结点的祖先:从根结点到该节点的 所有结点
- 结点的度:该节点有几个孩子,就是几度
- 树的度:树中,结点的度 最大的 称之为 树的度
- 树的深度/高度:从根节点开始,长度最长的那条路径,有几个结点就是 多高
- 树的性质
1、树中的结点树,等于所有结点的度数加1
2、度为 m 的树中,第i层上至多有 m 的(i - 1)次方个结点(i >= 1)
3、高度为 h 的 m 叉树中,至多有 (m 的 h 次方) / (m - 1)个结点 (二叉树再减一)
-
二叉树:有零个到两个结点的树,称之为 二叉树
-
二叉树的性质
- 性质一:在二叉树中 第 i 层上最多有 **2 i-1**个结点(i > 0)
- 性质二:深度为 k 的二叉树,最多有 2k-1个结点(k > 0)
- 性质三:树上的结点树为 n ,则边数一定为n - 1
- 性质四:任意一颗二叉树中,度为 0 的结点个数 = 度为 2 的节点个数 + 1
- 性质五:具有 n 个节点的 完全二叉树 的深度为**⌊log2n⌋**+ 1 (向下取整)
-
大顶堆 , 小顶堆
//大顶堆 每个根节点(所有的根节点)都大于它的子节点
ki >= k2i
ki >= k2i+1
//大顶堆 每个根节点(所有的根节点)都小于它的子节点
ki <= k2i
ki <= k2i+1
二叉树链式存储
- 结点的定于
typedef struct TreeNode{
char ch; //数据域
struct TreeNode *lchild; //左孩子指针
struct TreeNode *rchild; //右孩子指针
};
当没有 左右孩子结点的时候,左后孩子指针 为 NULL 值
-
遍历方式
- 先序遍历:根左右
- 中序遍历:左根右
- 后续遍历:左右根
-
先序遍历
void perOrdef(Node * root){ //root根节点的意思
//递归 结束的条件,也就是当一个结点 某个指针域为 NULL
if(root == NULL){
return;
}
printf("%c ",root->ch);
//递归调用左子树
perOrder(root->lchid);
//递归调用右子树
perOrder(root->rchild);
}
- 中序遍历
void inOrdef(Node * root){ //root根节点的意思
//递归 结束的条件,也就是当一个结点 某个指针域为 NULL
if(root == NULL){
return;
}
//递归调用左子树
perOrder(root->lchid);
printf("%c ",root->ch);
//递归调用右子树
perOrder(root->rchild);
}
- 后续遍历
void lastOrdef(Node * root){ //root根节点的意思
//递归 结束的条件,也就是当一个结点 某个指针域为 NULL
if(root == NULL){
return;
}
//递归调用左子树
perOrder(root->lchid);
//递归调用右子树
perOrder(root->rchild);
printf("%c ",root->ch);
}
- 根据遍历的序列 确定 二叉树 的形状
//1、先序和 中序 可以确定一棵二叉树
答:根据先序确定 根节点的位置,然很去中序中找到该节点左边元素都是左子树,右边元素都是右子树,一次重复上述过程,即可根据序列确定 二叉树形状。
(从前找根节点)
//2、后续和 中序 可以确定一颗二叉树
答:根据先序确定 根节点的位置,然很去中序中找到该节点左边元素都是左子树,右边元素都是右子树,一次重复上述过程,即可根据序列确定 二叉树形状。
(从后找根节点)
//3、先序和 后序 不能确定一颗二叉树
- 非递归中序遍历
void inOrder(Node * root){
//指针p 指向 根节点,并按照某种顺序游走于每一个结点
Node *p = root;
//建立栈,用来实现 递归
LinkStack s = init_LinkStack(); //初始化栈,初始化一个头结点出来
//p 不指向 NULL 并且 栈不空的时候
while(p || ! isEmpty_LinkStack(s)){
//根节点不空,进栈,让其指向左子树
if(p){
push_LinkStack(s , p);
p = p->lchild; //指向左子树
}else{
//定义一个指针 指向 栈顶元素 (就是 子树的根节点)
Node *top = top_LinkStack(s);
//元素出栈
pop_LinkStack(s);
printf("%c ",top->data);
p = top->rchild;
}
}
//销毁栈
destory_LinkStack(s);
}
-
如果有 n 个结点,则有n + 1个空指针域
-
线索 指向其前驱和后继的一个指针
-
孩子兄弟表示法:左边指针是孩子,右边指针是兄弟
二叉排序树
- 概念:是一颗空树,或者是满足以下性质的二叉树
- 左子树非空,左边结点 小于 根节点
- 右子树非空,右边节点 大于 根节点
- 中序遍历,可以实现 二叉排序树从小到大排序
//定义节点 结构体
typedef struct TreeNode{
int data;
struct TreeNode *lChild; //左孩子指针
struct TreeNode *rChild; //右孩子指针
}TreeNode;
TreeNode* searchTreeNode(TreeNode *root , int key){
//递归结束条件 root 为 NULL 相当于没有找到节点
if((root == NULL) || (key == root->data)){
return root;
}
else if(key < root->data){ //递归左子树查找
return searchTreeNode(root->lChild , key);
}
else{ //递归右子树查找
return searchTreeNode(root->rChild , key);
}
}
哈夫曼树(最小权值树)
- 路径:两个节点之间的 线就是我们的路径
- 节点的路径:从根节点到 此节点,之间有几根线,路径长度就是多少
- 树的路径长度:所有节点路径长度 之和 称之为 树的路径长度
- 权值:给这个节点赋一个数值,这个数值就是我们的权值
- 节点带权路径长度:路径长度 * 该节点权值
- 树的带权路径长度(WPL):所有叶子节点的带权路径长度之和
- 重点:哈夫曼树构造
//哈夫曼二叉树构造
1、每次从 序列中找出 权值最小的两个节点(一般,从左至右,从小到大)
2、生成一个新的节点,将这个节点放入 序列中,删除刚才的两个最小节点,再重复一过程
邻接矩阵
- 无向图对应的邻接矩阵是 对称矩阵
- 矩阵的大小 只与顶点个数有关 是一个 N*N阶矩阵
- 顶点的度:
- 入度:邻接矩阵对应于 列上值的 总和
- 出度:邻接矩阵对应于 行上值的 总和
邻接表
- 防止浪费空间(稀疏矩阵),但是效率相对于 邻接矩阵 较低
- 邻接表:顶点用一维数组存储,后面跟着单链表 存储 邻接点
- 邻接表 中 邻接点的个数 和 图中这个顶点 的出度有关
带权图
- 边 给一个值,称之为 边权,对应图 称之为 带权图,也称之为网
深度优先遍历DFS
- 不撞南墙不回头(遍历不唯一)
广度优先遍历算法BFS
- 相当于我们二叉树的层次遍历(用到队列,先进先出)
- 记得保持顺序
G = (V,E):G指的图 V指的顶点 E指的边
- 强连同图:任意顶点都能到达其他顶点,称之为,强连通图
最小生成树
-
生成树:顶点由边链接在一起,不存在回路的图
- 生成树顶点个数 和 图顶点个数相同
- 生成树(极小连通图)去掉一条边,则变成非连通图
- 连通图有 n 个顶点 则其 生成树 有 n - 1 条边
- 生成树 再加一条,必然形成回路
含有 n 个顶点 n - 1 条边的图,不一定是生成树
-
无向图的生成树文章来源:https://www.toymoban.com/news/detail-736380.html
- 深度优先生成树
- 广度优先生成树
-
最小生成树:边权值之和最小的树文章来源地址https://www.toymoban.com/news/detail-736380.html
普利姆算法(Prim)
- 普利姆算法 和 点 有关
- 每次去找和点 连接的最小的边(包括之前的点)
克鲁斯卡尔算法(Kruskal)
- 克鲁斯卡尔 和 边 有关
- 每次去找 边最小的 然后,两个顶点相连,依次构成最小生成树
最短路径
迪杰斯特拉(Dijkstra)
- 两点间最短路径
| 终点 | ||||||
|---|---|---|---|---|---|---|
| i | i=1 | i=2 | i=3 | i=4 | i=5 | i=6 |
| v1 | ||||||
| v2 | ||||||
| v3 | ||||||
| v4 | ||||||
| v5 | ||||||
| v6 | ||||||
| vj | ||||||
| 距离 | ||||||
弗洛伊德(Floyd)
- 所有顶点间的最短路径
- 两个矩阵,一个存储 权值,一个存储 路径
- 把所有的顶点 依次加入矩阵中,找最小的
拓扑排序
AOV网
- 顶点 表示 活动
- 弧 表示活动之间的优先制约关系
- 拓扑排序:前提有向 无环图
- 拓扑排序:找(无前驱)入度为 0 的结点 删除,循环上述过程即可
- 逆拓扑排序:找(无后继) 出度为 0 的结点 删除,循环上述过程即可
- 判断 AOV 网中是否有 环
到了这里,关于C语言数据结构与算法的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!