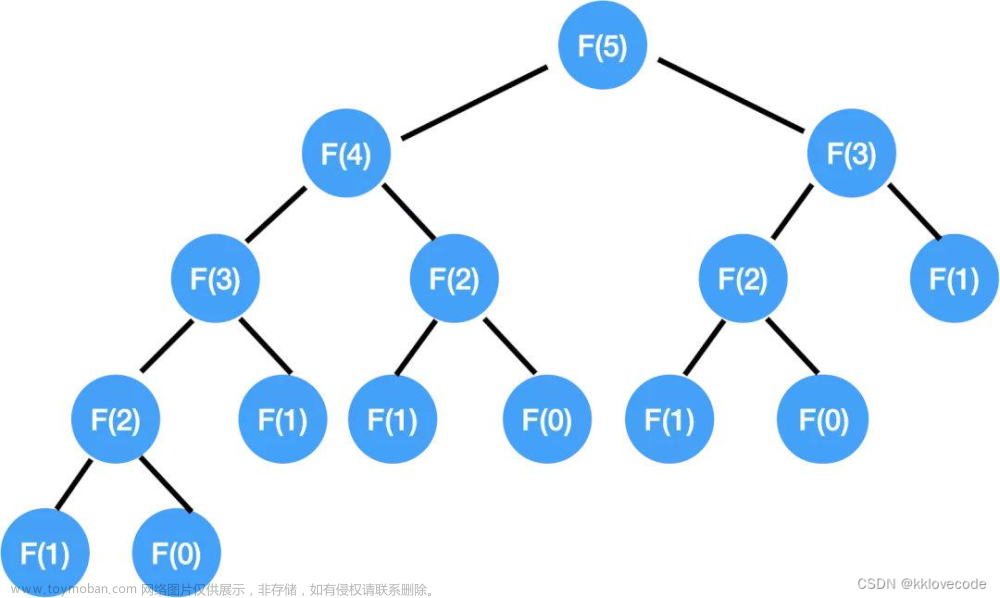
矩阵快速幂&斐波那契数列
矩阵快速幂:
- 快速地求出斐波那契数列中的每一项
- 可以快速地求出斐波那契数列的前n项的和
首先我们来看如何快速地求出斐波那契数列的第n项
1.快速求斐波那契数列的某一项
设
F
n
=
[
f
n
,
f
n
+
1
]
F_n = [f_n,f_{n+1}]
Fn=[fn,fn+1],构造这一个行向量,那么对于此,我们思考
F
n
F_n
Fn乘一个什么样的矩阵可以得到
F
n
+
1
F_{n+1}
Fn+1
显然:可以乘一个这样子的矩阵 
然后我们对这个递推的操作一直乘矩阵A,就可以推出最终
F
n
F_n
Fn的表达式:
即
F
n
=
F
0
∗
A
n
F_n = F_0 * A^n
Fn=F0∗An,求出
F
n
F_n
Fn之后,自然就得到
f
n
f_n
fn了!
2.快速求斐波那契数列的前n项和
法1
这个其实具体是一个推公式的过程,没有涉及到其他的东西,
设
S
n
=
f
0
+
f
1
+
f
2
+
.
.
.
+
f
n
S_n = f_0 + f_1 + f_2 +...+f_n
Sn=f0+f1+f2+...+fn
具体的公式为:
S
n
=
f
n
+
2
−
f
1
S_n = f_{n+2} - f_1
Sn=fn+2−f1 注意在我规定的斐波那契数列中,是从第0项开始的,公式具体的推导如下:
因此若要求斐波那契数列的前n项和,只需要求出
f
n
+
2
f_{n+2}
fn+2即可,那么这个问题其实又回到了求斐波那契数列的第n项,这样来看就很简单啦!
法2
构造一个新的行向量,
设
F
n
=
[
f
n
,
f
n
+
1
,
S
n
]
F_n = [f_n,f_{n+1},S_n]
Fn=[fn,fn+1,Sn] ,这里的
S
n
S_n
Sn就表示的是前n项的和,那么我们还是像开始一样思考一下如何构造矩阵,使得
F
n
F_n
Fn可以通过递推来求得。很容易推导出矩阵A的形式应该为:
因此我们可以通过此递推得到:
F
n
=
F
0
∗
A
n
F_n = F_0 * A^{n}
Fn=F0∗An
这样只要我们把
F
n
F_n
Fn求出来,就可以得到结果啦!
习题1:1303. 斐波那契前 n 项和
[1303. 斐波那契前 n 项和 - AcWing题库]:
附上AC代码:文章来源地址https://www.toymoban.com/news/detail-736656.html
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long LL;
LL n,m;
const int N = 3;
int a[N][N] = {
{0,1,0},
{1,1,1},
{0,0,1},
};
// 矩阵乘法:计算行向量 * 一个矩阵
void mul(int c[],int a[],int b[][N]){ // 计算 a[] * b[][] -> 即:f1[] * a[][] 之后的值
int tmp[N] = {0}; // 表示最后的答案数组
for(int i = 0;i < N;i++){ // i表示答案的那一列
// c[i] 表示的值应该等于 a中的每一个数 * b中第i列的那个数 的求和
for(int j = 0;j < N;j++){ // j枚举的就是a中的每一个数
tmp[i] = (tmp[i] + (LL)a[j] * b[j][i]) % m;
}
}
memcpy(c,tmp,sizeof(tmp));
}
// 矩阵乘法:计算一个矩阵 * 一个矩阵
void mul(int c[][N],int a[][N],int b[][N]){
int tmp[N][N] = {0};
for(int i = 0;i < N;i++){
for(int j = 0;j < N;j++){ // 枚举计算tmp[i][j]
// 计算c[i][j]需要枚举的就是a[i][]的那一行的数 * b[][j]那一列的数
for(int k = 0;k < N;k++){
tmp[i][j] = (tmp[i][j] + (LL)a[i][k] * b[k][j]) % m;
}
}
}
memcpy(c,tmp,sizeof(tmp));
}
int main()
{
cin >> n >> m;
int f1[N] = {1,1,1}; // 表示的是 [f1,f2,S1]
// Fn为向量
// Fn = F1 * A^n-1 次幂
LL k = n - 1;
// 写快速幂
while(k){
if(k & 1) mul(f1,f1,a); // f1[] = f1[] * a[][]
k >>= 1;
mul(a,a,a); // a[][] = a[][] * a[][]
}
cout << f1[2] << endl;
return 0;
}
3.快速求斐波那契数列前n项的平方和
如何快速地求出
f
0
2
+
f
1
2
+
.
.
.
+
f
n
2
f_0^2 + f_1^2 + ... + f_n^2
f02+f12+...+fn2 呢?
先给出结论:
f
0
2
+
f
1
2
+
.
.
.
+
f
n
2
=
f
i
∗
f
i
+
1
f_0^2 + f_1^2 + ... + f_n^2 = f_i * f_{i + 1}
f02+f12+...+fn2=fi∗fi+1
下面给出证明的过程:
其实只要知道了结论,具体做起题目来就简单多了!
习题2:斐波那契的秘密
http://csoj.scnu.edu.cn/problem/S0413文章来源:https://www.toymoban.com/news/detail-736656.html
附上AC代码:
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 2,mod = 1e9+7;
int a[N][N] = {
{0,1},
{1,1},
};
int f0[N];
int backup[N][N];
int t;
int n;
int l1,r1,l2,r2;
void mul(int c[][N],int a[][N],int b[][N]){
int tmp[N][N] = {0};
for(int i = 0;i < N;i++){
for(int j = 0;j < N;j++){
for(int k = 0;k < N;k++){
tmp[i][j] = (tmp[i][j] + (LL)a[i][k] * b[k][j]) % mod;
}
}
}
memcpy(c,tmp,sizeof(tmp));
}
void mul(int c[],int a[],int b[][N]){
int tmp[N] = {0};
for(int i = 0;i < N;i++){
for(int j = 0;j < N;j++){
tmp[i] = (tmp[i] + (LL)a[j] * b[j][i]) % mod;
}
}
memcpy(c,tmp,sizeof(tmp));
}
LL F(int x){ // 求Fx Fn = F0 * A^n次幂
memcpy(a,backup,sizeof(backup));
f0[0] = f0[1] = n;
while(x){
if(x & 1) mul(f0,f0,a);
x >>= 1;
mul(a,a,a);
}
return (LL)f0[0];
}
LL qmi(LL a,LL k,LL p){
LL res = 1;
while(k){
if(k & 1) res = res * a % p;
k >>= 1;
a = a * a % p;
}
return res;
}
int main()
{
cin >> n;
int t;
cin >> t;
memcpy(backup,a,sizeof(a));
while(t--){
cin >> l1 >> r1 >> l2 >> r2;
// cout << F(l1 - 1) << " " << F(l1) << " " << F(r1) << " " << F(r1+1) << endl;
// cout << F(r2 + 2) << " " << F(l2 + 1) << endl;
LL fenzi = ((F(r1) * F(r1 + 1) % mod - F(l1 - 1) * F(l1) % mod) % mod + mod) % mod;
// cout << "fenzi = " << fenzi << endl;
LL fenmu = ((F(r2 + 2) - F(l2 + 1)) % mod + mod) % mod;
// 然后求逆元
LL fenmu2 = qmi(fenmu,mod-2,mod);
// cout << "分母 = " << fenmu2 << endl;
cout << fenzi * fenmu2 % mod << endl;
}
return 0;
}
到了这里,关于矩阵快速幂&斐波那契数列的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!