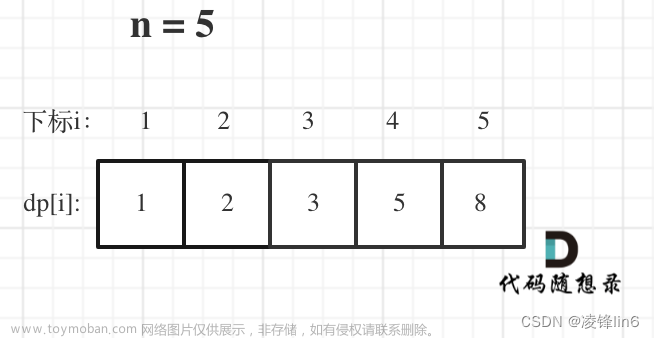
斐波那契数 (通常用 F(n) 表示)形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始,后面的每一项数字都是前面两项数字的和。也就是:
F(0) = 0,F(1) = 1 F(n) = F(n - 1) + F(n - 2),其中 n > 1
给定 n ,请计算 F(n) 。
示例 1:
输入:n = 2 输出:1 解释:F(2) = F(1) + F(0) = 1 + 0 = 1
示例 2:
输入:n = 3 输出:2 解释:F(3) = F(2) + F(1) = 1 + 1 = 2
示例 3:文章来源:https://www.toymoban.com/news/detail-736939.html
输入:n = 4 输出:3 解释:F(4) = F(3) + F(2) = 2 + 1 = 3
提示:文章来源地址https://www.toymoban.com/news/detail-736939.html
0 <= n <= 30
class Solution {
public:
int fib(int n) {
//定义dp数组的意思
//状态
//初始化
//遍历顺序
//dp数组值是否符合
if(n < 2) return n;
// 表示第一个斐波那契数为dp[i];
vector<int>dp(n+1); // 因为下面直接访问dp[0]和dp[1],所以得先加内存。
dp[0] = 0;
dp[1] = 1;
for(int i = 2;i <= n;i++){
dp[i] = dp[i-1]+dp[i-2];
}
return dp[n];
}
};到了这里,关于509. 斐波那契数的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!