一、什么是高精度
高精度本质上是一种计算,由于int型和long long型的存储的数据大小有限。在有符号定义的情况下,int型为2的31次方减1;在无符号定义的情况下,lint型为2的32次方。因此过于巨大的数无法展示,这就用到了高精度来计算,其原理为将很大的数一位一位存在数组中,最后输出数组。
二、高精度加法
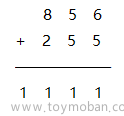
说起来也觉得有些可笑,但确实如此,高精度加法我们运用的是小学的数列式来理解。


如左图所示,我们首先将1加7得8,6加7为13,1加6为7;然后发现13大于10,因此要进1。所以,7需要加1变为8。写成代码如上右图所示,给大家解释一下吧,aar1数组表示1,6,7三位数;arr2数组表示6,7,1三位数,值得注意的一点是在数组中应倒置这样的话便于计算;arr3数组表示的是最后的结果。第一行代码是将1加7相加得到的结果(一会儿再解释为啥还要加arr3),第二行代码是将大于10的部分交于数组的下一个变量(体现在数学中也就是进位);第三行代码是得出结果(如6加7得13,经过此步后便得到3)。由于这只是得到某一位的结果,因此循环才能得到最终的结果,上面未解释的arr3则是为了防止可能由于前一位进1而导致本身不再是0。给大家上代码理解一下吧。
# include <stdio.h>
# include <string.h>
int main ()
{
int max(int x,int y);
//利用字符串形式输入,否则数字太大,整形放不下。
char ch1[505]="123",ch2[505]="123";
int arr1[505]={0},arr2[505]={0},arr3[505]={0};
scanf("%s",&ch1);scanf("%s",&ch2);
int sz1=strlen(ch1);int sz2=strlen(ch2);
//因为要循环相加,sz3求循环条件的,由于最后一位相可能大于10,因此先进1
int sz3=max(sz1,sz2)+1;
//将字符串转变为数组形式存储
for(int i=0;i<sz1;i++)
{
arr1[sz1-i]=ch1[i]-'0';
}
for(int i=0;i<sz2;i++)
{
arr2[sz2-i]=ch2[i]-'0';
}
//高精度加法主体
for(int i=1;i<=sz3;i++)
{
arr3[i]=arr3[i]+arr1[i]+arr2[i];
arr3[i+1]=arr3[i]/10;
arr3[i]=arr3[i]%10;
}
//判断数组最后一位是否为0,不是的话减去0,并且sz3还应大于0,否则可能什么结果也不输出(当输入为0时)
if(arr3[sz3]==0&&sz3>0) sz3--;
输出
for(int i=sz3;i>0;i--)
{
printf("%d",arr3[i]);
}
return 0;
}
int max(int x,int y)
{
int f;
if(x>y) f=x;
else f=y;
return f;
}三、高精度减法
高精度减法其实和加法差不多,不过需要注意的一点是应先判断大小,应该用大的减小的,计算机不会算小的减大的,下图是高精度减法主体。

高精度减法也是循环相减的,一位一位减。给大家解释一下高精度减法主体的代码吧,先判断一下减数和被减数的大小关系,如果减数大于被减数,需要进一,也就是上一位的减数减一,而这一位加10,这就是第二三行代码的意思,最后一行则是相减得到的数,给大家上整体的代码看看吧。
# include <stdio.h>
# include <string.h>
int main ()
{
int compare(char a1[10090],char a2[10090],int sz1,int sz2);
char a1[10090]="123",a2[10090]="123";
int b1[10090]={0},b2[10090]={0},b3[10090]={0};
scanf("%s",&a1);scanf("%s",&a2);
int sz1=strlen(a1);
int sz2=strlen(a2);
//比较大小
int m=compare(a1,a2,sz1,sz2);
//判断是否改变两个的位置
if(m==0)
{
char q[10090]="123";
strcpy(q,a1);
strcpy(a1,a2);
strcpy(a2,q);
}
int sz3=strlen(a1);
int sz4=strlen(a2);
//将字符串变为数组形式
for(int i=0;i<sz3;i++)
{
b1[sz3-i]=a1[i]-'0';
}
for(int i=0;i<sz4;i++)
{
b2[sz4-i]=a2[i]-'0';
}
//高精度减法主体
for(int i=1;i<=sz3;i++)
{
if(b1[i]<b2[i])
{
b1[i+1]--;
b1[i]=b1[i]+10;
}
b3[i]=b1[i]-b2[i];
}
//判断是否为0
while(b3[sz3]==0&&sz3>1) sz3--;
//判断是否要变为负数
if(m==0) printf("-");
//输出0
for(int i=sz3;i>0;i--)
{
printf("%d",b3[i]);
}
return 0;
}
int compare(char a1[10090],char a2[10090],int sz1,int sz2)
{
if(sz1>sz2) return 1;
else if(sz1<sz2) return 0;
else
{
for(int i=0;i<sz1;i++)
{
if(a1[i]>a2[i]) return 1;
else if(a1[i]<a2[i]) return 0;
else continue;
}
}
}四、高精度乘法
高精度乘法的本质也是利用小学数学的列式来解决问题 

给大家解释一下代码吧,大家经过高精度加法和高精度减法的代码应该也是对高精度了解的比较清楚了,给大家简单介绍一下高精度乘法吧,如上左图所示,假设a为一个数组b为一个数组,c为一个数组,通过上图可以看出,乘法每一个相乘的结果的下标,为上面两个的下标之和减1;如c3中的2是a2和b2中2和2相加减1得,c4中的4是由a4和b1或者b4和c1中4和1相加减1得到的。这就是来源。下面则是我们来实现这个代码,相同的是,这也是一个循环(嵌套循环,大家可以看代码),我只是把主体写出。
# include <stdio.h>
# include <string.h>
int main ()
{
//定义变量
char a1[2005]="123";
char a2[2005]="123";
int b1[2005]={0},b2[2005]={0},b3[2005]={0};
scanf("%s",a1);scanf("%s",a2);
int sz1=strlen(a1);int sz2=strlen(a2);
//将字符串变为数组
for(int i=0;i<sz1;i++)
{
b1[sz1-i]=a1[i]-'0';
}
for(int i=0;i<sz2;i++)
{
b2[sz2-i]=a2[i]-'0';
}
//循环条件
int sz3=sz1+sz2;
//循环主体
for(int i=1;i<=sz1;i++)
{
for(int j=1;j<=sz2;j++)
{
b3[i+j-1]=b3[i+j-1]+b1[i]*b2[j];
b3[i+j]=b3[i+j]+b3[i+j-1]/10;
b3[i+j-1]=b3[i+j-1]%10;
}
}
if(b3[sz3]==0&&sz3>0) sz3--;
//输出
for(int i=sz3;i>0;i--)
{
printf("%d",b3[i]);
}
return 0;
}五、实例(求函数阶乘和)
·
文章来源地址https://www.toymoban.com/news/detail-737214.html
这里我用了洛谷的一道题来举例,结合了高精度加法和高精度减法,还是比较有难度的。即使我们可以掌握高精度这个知识点,但能AC这道题还是不容易的。先给大家上代码再解释吧。
文章来源:https://www.toymoban.com/news/detail-737214.html
# include <stdio.h>
int main ()
{
int n,cnt=1;scanf("%d",&n);
int a[10000]={0},b[10000]={0};
for(int i=0;i<10000;i++) a[i]=0;
for(int i=0;i<10000;i++) b[i]=0;
a[1]=1;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=cnt;j++)
{
a[j]*=i;
}
for(int q=1;q<=cnt;q++)
{
if(a[q]<10) continue;
int x=q;
while(x<=cnt)
{
if(a[cnt]>9) cnt++;
a[x+1]=a[x+1]+a[x]/10;
a[x]=a[x]%10;
x++;
}
}
for(int h=1;h<=cnt;h++)
{
b[h]=a[h]+b[h];
if(b[cnt]>10) cnt++;
b[h+1]=b[h+1]+b[h]/10;
b[h]=b[h]%10;
}
}
for(int i=cnt;i>0;i--)
{
printf("%d",b[i]);
}
}怎么说呢,这个解释起来还是比较麻烦的,我们先输入n,然后就进入循环主体了,先for循环吧,将每一位数字都乘以i;然后再进入另一个循环,先判断每一位数是否大于9,如果大,肯定要进1,因此要进入另一个循环。然后就是进入一个while循环,判断最后一位是否大于9,如果大于,那么肯定要进,为防止溢出,我们就需要将数组加1,然后就是进入高精度乘法主体,然后再进入高精度加法主体,最后循环完输出即可。
写的不好,如果我有什么理解,一定会及时更改,谢谢各位的观看。
到了这里,关于算法之高精度(含实例与详解)C语言的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!