【密码学】一篇文章讲透数字签名-Toy模板网

这篇具有很好参考价值的文章主要介绍了【密码学】一篇文章讲透数字签名。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

【密码学】一篇文章讲透数字签名

数字签名介绍

数字签名（又称公钥数字签名）是只有信息的发送者才能产生的别人无法伪造的一段数字串，这段数字串同时也是对信息的发送者发送信息真实性的一个有效证明。它是一种类似写在纸上的普通的物理签名，但是在使用了公钥加密领域的技术来实现的，用于鉴别数字信息的方法。一套数字签名通常定义两种互补的运算，一个用于签名，另一个用于验证。数字签名是非对称密钥加密技术与数字摘要技术的应用。

数字签名可以识别消息是否被篡改，并验证消息的可靠性，也可以防止否认。在之前的博客文章中，我们介绍过消息认证码，它也可以防止消息被篡改，验证消息可靠性。而数字签名与消息认证码的最大不同在于，数字签名算法可以防止否认，因为私钥只有签名者持有，而消息认证码中的密钥由双方共享。常用的数字签名方法有三种，分别是RSA、 DSA和ECDSA。

数字签名原理

数字签名类似于现实世界中的盖章和签字，它具有以下四大特征：

可验证性——接收者可以验证发送者签名的真实性和有效性；
不可伪造性——除签名者之外，任何人不可伪造签名；
不可否认性——发送方不能否认自己所发送的签名；
数据完整性——能够提供对所签消息的完整性检验。

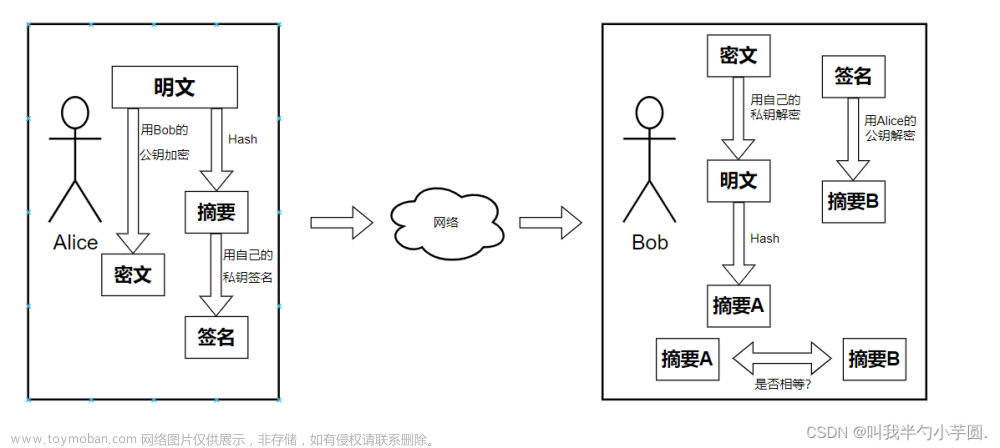
下面通过一个示例来说明数字签名是如何防止否认的：

数字签名的三种方法,物联网安全,密码学,网络,安全

Alice通过密钥生成算法生成密钥对；
2） Alice将公钥发送给Bob，私钥自己保留；
3） Alice使用单向数列函数计算出合同的摘要值；
4） Alice使用私钥对消息摘要值进行签名；
5） Alice将合同和签名值分别发送至Bob；
6） Bob使用单向散列函数计算出合同的消息摘要值；
7） Bob使用Alice的公钥对签名进行验证，若验证通过则说明合同内容完整且来自于Alice。

从本应用场景中可以看出，虽然数字签名的工作模式与消息认证码较为相似，但不同的是数字签名可防止否认。消息认证码使用的密钥为对称密钥，如果基于消息认证码完成消息的认证过程，一旦Alice否认曾经向Bob发送过预订合同，那么Bob将无法对Alice进行指控。而数字签名算法中私钥只有Alice持有，其他人无法对签名进行伪造，这一特点也使得Alice无法对这一过程进行否认。

RSA数字签名算法

RSA数字签名算法基于RSA密钥系统实现，在第8章中已经详细介绍了RSA算法。 RSA数字签名过程与RSA加解密过程较为相似，但公钥和私钥的使用方法却存在明显区别。为了方便描述RSA数字签名过程，此处依然借助假想场景加以说明，在假想场景中：
1） Alice通过RSA密钥生成算法生成密钥对；
2） Alice将公钥发送给Bob，私钥自己保留；
3） Alice使用RSA私钥对消息进行加密操作，并将消息和签名结果分别发送给Bob；
4） Bob使用RSA公钥对签名进行解密操作，判断解密结果和消
息是否一致。

此处Alice使用私钥对消息执行加密操作，该加密操作可理解为对消息进行数字签名，该私钥可称为签名密钥； Bob收到消息之后使用Alice的公钥执行解密操作，该解密操作可理解为对消息执行数字签名验证，该公钥可称为验证密钥。总之，在RSA数字签名中，私钥用于加密消息，公钥用于解密消息；而在RSA加密中，公钥用于加密消息，而私钥用于解密消息。无论如何，公钥总是可以公开的，而私钥却不能泄露。

RSA数字签名详细说明

RSA签名

RSA数字签名和RSA加密过程恰好相反，签名过程使用私钥对数据执行加密操作， RSA数字签名表达式如下，其中s为签名结果， m为消息（消息可以是明文也可以是消息摘要）。

s ≡ mdmod n

###RSA验证签名

同样，验证签名过程使用公钥对签名数据进行解密， RSA验证签名表达式如下，其中s为签名结果， m’为解密结果。验证签名过程判断m’≡mmod n，成立则为有效签名，不成立则签名无效。

m' ≡ semod n

由于参数e的值远小于参数d，所以RSA验证签名的计算量小于RSA签名，也就说RSA验证签名速度快于签名速度。

ECDSA数字签名

ECDSA算法基于椭圆曲线离散对数问题，使用较短的密钥长度便可提供与RSA签名算法或DSA算法等同的安全等级，密钥长度为160_{256位的椭圆曲线算法与密钥长度为1024}3072位的非椭圆曲线算法安全性相同。椭圆曲线的基础知识可以参考我之前的博客。

ECDSA数字签名算法和DSA算法在概念上有紧密联系，但其计算过程是在椭圆曲线群上完成的，所以计算过程相差较大。 ECDSA算法与DSA算法相似，该算法只能提供数字签名功能，而不能用于加密或密钥交换。

ECDSA生成签名

ECDSA的签名结果由两部分构成： r和s。其中r和s的长度与n相同，例如在secp256r1曲线中， n的长度为256比特， r和s也分别为256比特，不使用任何编码方式的情况下签名总长度为512比特。假设消息为M，单向散列函数为HASH()。使用ECDSA对消息进行签名的计
算过程如下：
1）选择一个随机数k，满足条件0<k<n；
2）计算R=k·G；
3）计算z=HASH(M)；
4）设置r=xR， xR为点R的横坐标；
5）计算s≡(z+d·r)k-1mod n；
6）得到签名(r,s)。

ECDSA验证签名

在验证签名之前需确保已经得到签名者的公钥、消息以及签名信息(r,s)。验证签名的过程如下：
1）计算w≡s-1mod n；
2）计算z=HASH(M)；
3）计算u1≡(wz)mod n；
4）计算u2≡(wr)mod n；
5）计算P=u1·g+u2·Q；
6）如果xP≡r mod n，则签名有效，否则签名无效，其中xP为点P的横坐标。文章来源地址https://www.toymoban.com/news/detail-738376.html

到了这里，关于【密码学】一篇文章讲透数字签名的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！