数据结构与算法之排序: 计数排序 (Javascript版)-Toy模板网

这篇具有很好参考价值的文章主要介绍了数据结构与算法之排序: 计数排序 (Javascript版)。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

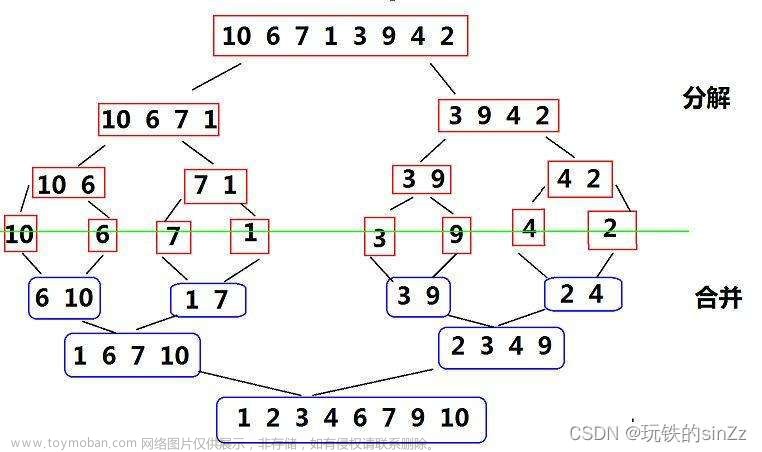
排序

排序：把某个乱序的数组变成升序或降序的数组 (这里用数组来做举例)

计数排序

核心思想：通过计数而非比较来进行排序，借助数组下标本身就是有序的原理实现
适用范围：较小的非负整数序列和最小值和最大值之间的数字范围比较合适
基数排序需要新增一个计数数组(待累计数组)
- 计数数组：即新的临时的初始化数组用于计数，需要找到原始数组中最大的值，再加1，才是这个数组的长度，存储 [0 ~ max]
- 累计数组：是由计数数组计算后得到的，下标是原数组的值，元素值是累计的个数，即重复的个数

算法实现

1 ）基础版本

function countSort(list: number[]) {
	const len: number = list.length;
	if (len < 2) return;
	// 获取最大值
	// const max = Math.max.apply(null, list);
	const max: number = Math.max(...list);
	// 初始化计数数组
	const countList: number[] = new Array(max + 1).fill(0); // 数组大小，存放[0~max]
	// 对原数组的数据在计数数组中累计，原数组的值是计数数组的下标
	let i: number;
	for(i = 0; i < len; i++) countList[list[i]]++; // 遍历完成后计数数组就变成了累计数组
	// 基于累计数组生成排好序的数组，这里利用了下标即是有序的原理
	i = 0; // 重新使用i
	for(let j: number = 0; j < max + 1; j++) {
    	// 内层循环不会到n, 一般是常数级别的，但是这样写似乎也不是太好，嵌套会增加时间复杂度
		for (let k: number = 0; k < countList[j]; k++) list[i++] = j; // 这里j就是下标，其实就是原数组的值
	}
}

const list = [2, 3, 8, 7, 1, 2, 2, 2, 7, 3, 9, 8, 2, 1, 4, 2, 4, 6, 9, 2];
countSort(list);
console.log(list); // [1, 1, 2, 2, 2, 2, 2, 2, 2, 3, 3, 4, 4, 6, 7, 7, 8, 8, 9, 9]

2 ）优化版本：优化时间复杂度(空间换时间)

function countSort(list: number[]): number[] {
	const len: number = list.length;
	if (len < 2) return list;
	// 获取最大值和最小值
	// const max = Math.max.apply(null, list);
	// const min = Math.min.apply(null, list);
	const max: number = Math.max(...list);
	const min: number = Math.min(...list);
	// 初始化计数数组
	const countList: number[] = new Array(max - min + 1).fill(0);
	// 对原数组的数据在计数数组中累计，原数组的值是计数数组的下标
	for(let i: number = 0; i < len; i++) countList[list[i] - min]++; // 遍历完成后计数数组就变成了累计数组
	// 基于累计数组生成排好序的数组，这里利用了下标即是有序的原理
	let result: number[] = [];
	for(let j: number = 0; j < max + 1; j++) {
		if (!countList[j]) continue;
		countList[j] > 1 ? (result = result.concat(new Array(countList[j]).fill(j + min))) : result.push(j + min);
	}
	return result; // 替换
}

const list: number[] = [102, 103, 108, 107, 101, 102, 102, 102, 107, 103, 109, 108, 102, 101, 104, 102, 104, 106, 109, 102];
const result: number[] = countSort(list);
console.log(result); // [101, 101, 102, 102, 102, 102, 102, 102, 102, 103, 103, 104, 104, 106, 107, 107, 108, 108, 109, 109]

3 ）优化版本：优化时间复杂度(空间换时间) + 优化存储空间

function countSort(list: number[]) {
	const len: number = list.length;
	if (len < 2) return list;
	// 获取最大值和最小值
	const max: number = Math.max(...list);
	const min: number = Math.min(...list);
	// 初始化计数数组
	const countList: number[] = new Array(max - min + 1).fill(0);
	// 对原数组的数据在计数数组中累计，原数组的值是计数数组的下标
	for(let i: number = 0; i < len; i++) countList[list[i] - min]++; // 遍历完成后计数数组就变成了累计数组
	// 基于累计数组生成排好序的数组，这里利用了下标即是有序的原理
	let str: string = ''; // 用字符串来处理
	for(let j: number = 0; j < max - min + 1; j++) {
		if (!countList[j]) continue;
		str += countList[j] > 1 ? ((j + min) + ',').repeat(countList[j]) : (j + min) + ',';
	}
	str = str.substring(0, str.length - 1); // 最后一个 , 是多余的
	return str.split(',').map(item => Number(item));
}

const list: number[] = [102, 103, 108, 107, 101, 102, 102, 102, 107, 103, 109, 108, 102, 101, 104, 102, 104, 106, 109, 102];
const result: number[] = countSort(list);
console.log(result); // [101, 101, 102, 102, 102, 102, 102, 102, 102, 103, 103, 104, 104, 106, 107, 107, 108, 108, 109, 109]

4 ）优化版本：优化时间复杂度(累计数组变位置数组，基于差值和位置来对应顺序)文章来源地址https://www.toymoban.com/news/detail-738400.html

function countSort(list: number[]) {
	const len: number = list.length;
	if (len < 2) return;
	// 获取最大值和最小值
	const max: number = Math.max(...list);
	const min: number = Math.min(...list);
	// 初始化计数数组
	const countList: number[] = new Array(max - min + 1).fill(0);
	// 初始化目标数组
	const result: number[] = new Array(len);
	// 对原数组的数据在计数数组中累计，原数组的值是计数数组的下标
	for(let i: number = 0; i < len; i++) countList[list[i] - min]++; // 遍历完成后计数数组就变成了累计数组
	// 计算位置: 由上面的累计结果，计算累加后的位置, countList数组从累计数组，变成了位置数组
	for(let j: number = 1; j < max - min + 1; j++) {
		countList[j] += countList[j - 1];
	}
	// 根据累加后的位置, 将原数组中的数据按照位置进行分配，就得到排好序的数组，备注：数据可能重复，使用过的数据记得-1，从后向前遍历更好理解
	for (let k: number = len - 1; k >= 0; k--) {
		const currentIndex = countList[list[k] - min] - 1;
		result[currentIndex] = list[k]; // 将原数组的当前元素整合到 result数组对应的位置之中
		countList[list[k] - min] --; // 使用一次后，累计的数量自减，防止重复使用导致错误
	}
	list.splice(0, len, ...result); // 优化下方式，不用return, 直接替换
}

const list: number[] = [102, 103, 108, 107, 101, 102, 102, 102, 107, 103, 109, 108, 102, 101, 104, 102, 104, 106, 109, 102];
countSort(list);
console.log(list); // [101, 101, 102, 102, 102, 102, 102, 102, 102, 103, 103, 104, 104, 106, 107, 107, 108, 108, 109, 109]

总结

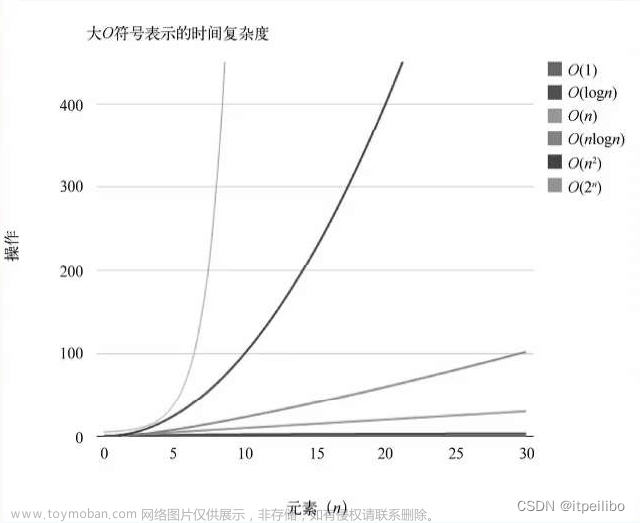
计数排序的适用范围有限：最优版时间复杂度可降低到 O(n), 是最快的排序算法, 但是有两个前提需要满足
- 1）需要排序的元素必须是非负整数(下标不能是负数和小数)
  - 如果是小数，需要将全部元素同等扩大到整数，之后再回归到小数
  - 一般不考虑这种小数场景
- 2）排序元素的取值要在一定范围内，并且比较集中(量大，范围小)
满足以上两个条件，才能最大发挥出计数排序的优势, 否则不适用
计数排序的缺点
- 基础版空间浪费，优化版解决了这个问题
- 将数组长度定为 max-min+1, 即不仅要找出最大值，还要找出最小值
缺点弥补：根据两者的差来确定计数数组的长度则可弥补之
计数排序是非常稳定的排序算法，但是适用场景确实有限
计数排序是一种桶排序的思想