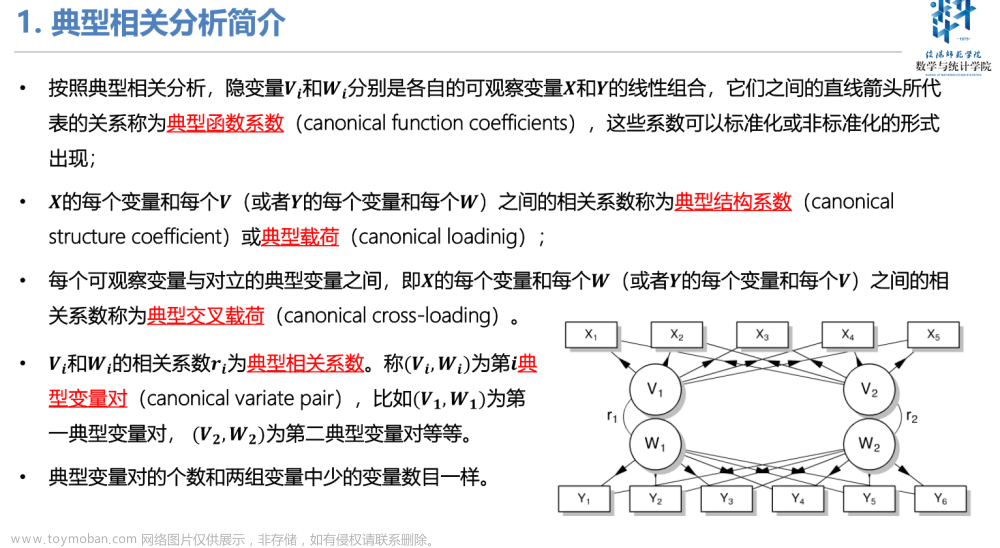
目录
一、简介
二、Person相关系数
三、相关性可视化
四、皮尔逊相关系数的理解误区
五、对皮尔逊相关系数的两点总结
六、Person系数习题
七、Person系数假设检验适用前提
八、Spearman相关系数
九、Spearman相关系数假设检验
十、两者适用性
一、简介
本讲我们介绍两种最常用的相关系数:person相关系数和spearman相关系数。他们用来衡量两个变量之间的相关性大小,根据数据的不同特点,我们要选择不同的系数进行计算和分析(选择哪个系数也是论文中最容易出错的地方)。实际中,更多会使用spearman相关系数,因为person系数的限制条件会更多。
二——七:Perosn相关系数
八——九:Spearman相关系数
十:两者适用性
二、Person相关系数
1.总体Person相关系数
如果两组数据X:{X1,X1,```,Xn}和Y:{Y1,Y2,```,Yn}是总体数据(比如普查结果)
那么总体均值为:
总体协方差:
总体Person相关系数为:
其中,,分别是X的标准差和Y的标准差,
最终可以证明:,当, 则 ;
2.样本Person相关系数
如果两组数据X:{X1,X1,```,Xn}和Y:{Y1,Y2,```,Yn}是样本数据(比如调查得到的数据)
样本均值:
样本协方差:
样本Person相关系数:
其中,
三、相关性可视化
通过绘制散点图可以很容易地判定两个数据对象x和y之间的相关性:
四、皮尔逊相关系数的理解误区
先给出五张图:

图一、二、三、四

图五
对于上面四个图的数据来说,Person系数都是0.816 ;
图一:还可以理解,大多点确实分布在拟合线的周围
图二:表现出的是二次函数的点
图三:有一个异常值,导致拟合线受到影响
图四:有一个异常值,但是拟合线相当离谱! (假设把异常值去了,那么X4和Y4可以说是毫无关系的)
图五:显然根据生活经验,冰淇淋销量和温度是有很大的相关性的,但是Person却是0
虽然四幅图的分布都完全不同,但是他们的Person系数确实都是0.816!
接下来给出解释:相关系数只是用来衡量两个变量线性相关程度的指标;也就是说,在使用Person系数之前,必须先确认这两个变量是线性相关的,然后这个相关系数才能告诉你这两个变量的相关程度。
根据上述解释的原理,我们再回过头解释这四幅图:
- 非线性先关也会导致线性相关系数很大,如图二
- 离群点(异常值)对相关系数的影响很大,例如图三,去掉离群点之后的相关系数为0.98
- 如果两个变量的相关系数很大也不能说明两者相关,比如图四,有可能是受到了异常值的影响
- 相关系数计算为0,只能说明不是线性相关,但说不定会有更复杂的关系(非线性相关),比如图五
五、对皮尔逊相关系数的两点总结
(1)如果两个变量本身就是线性的关系,那么皮尔逊相关系数的绝对值大的就是相关性强,小的就是相关性弱。
(2)在不确定两个变量是什么关系的情况下,即使算出了Person系数发现很大,也不能说明两个变量线性先关,甚至不能说明这两个变量是相关的。因此我们必须要画出散点图来看才行。
(3)事实上,比起相关系数的大小,在实际中我们更关注显著性(假设检验)。
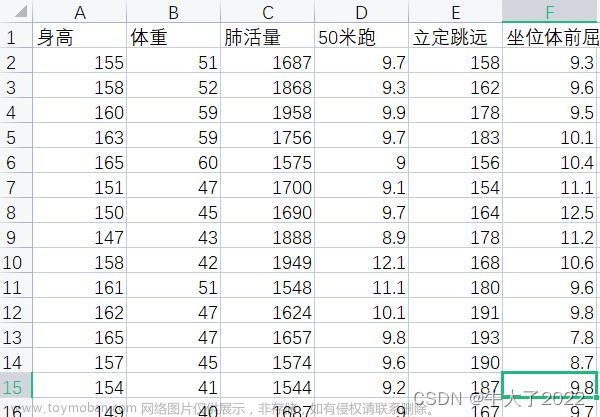
六、Person系数习题
现有某中学八年级女生的体测数据样本,见下表,试计算各变量之间的Person相关系数。

方法一:通过matlab代码计算(具体模板代码可以三连后私信我)
方法二:通过spss 24.0版本 软件快速得到结果(软件破解版安装可以三连后私信我)
通过spss得到如下散点图结果:

通过spss得到如下描述性统计:

通过将结果导入excel,使用excel的色阶工具得到如下比较美观的图(可以放到论文中):

七、Person系数假设检验适用前提
- 实验数据通常假设是成对的来自正态分布的总体
- 实验数据之前的差距不能太大
- 每组样本之间是相互独立的
八、Spearman相关系数
在matlab中的定义:等级之间的皮尔逊相关系数,如下图

九、Spearman相关系数假设检验
小样本情况下(n ≤ 30):直接查下图临界表即可
大样本情况下:,为算出的斯皮尔曼相关系数,n表示样本数量,我们计算出检验值,并求出对应的p值与0.05相比即可。如下图: 文章来源:https://www.toymoban.com/news/detail-738665.html
文章来源:https://www.toymoban.com/news/detail-738665.html
十、两者适用性
- 连续数据、正态分布、线性关系,用person系数最为恰当,效率比spearman高
- 上述任一条件不满足,就用spearman相关系数,不用person相关系数
- 两个定序数据之间也使用spearman相关系数,不用person相关系数
相关完整的配套代码和完整文档,可以关注后私信我免费领取文章来源地址https://www.toymoban.com/news/detail-738665.html
到了这里,关于数学建模冲国奖之——Person相关系数和Spearman相关系数的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!