【算法】约瑟夫环问题解析与实现-Toy模板网

这篇具有很好参考价值的文章主要介绍了【算法】约瑟夫环问题解析与实现。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

导言

约瑟夫环（Josephus Problem）是一个经典的数学问题，涉及一个编号为 1 到 n 的人围成一圈，从第一个人开始报数，报到某个数字 m 的人出列，然后再从下一个人开始报数，如此循环，直到所有人都出列。本篇博客将详细解析约瑟夫环问题，并使用 Python 实现算法。

问题分析

在约瑟夫环问题中，有两个变量需要确定：人数 n 和报数的数字 m。当给定 n 和 m 后，需要确定最后留下的人的编号。例如，当 n=7，m=3 时，约瑟夫环问题的过程如下：

1 2 3 4 5 6 7（初始状态）
1 2 4 5 6 7（第三个人出列，报数到 3）
1 2 4 5 7（第六个人出列，报数到 3）
1 4 5 7（第二个人出列，报数到 3）
1 4 5（第五个人出列，报数到 3）
4 5（第一个人出列，报数到 3）
4（最后一个人出列，报数到 3）

因此，最后留下的人的编号为 4。

解决方案

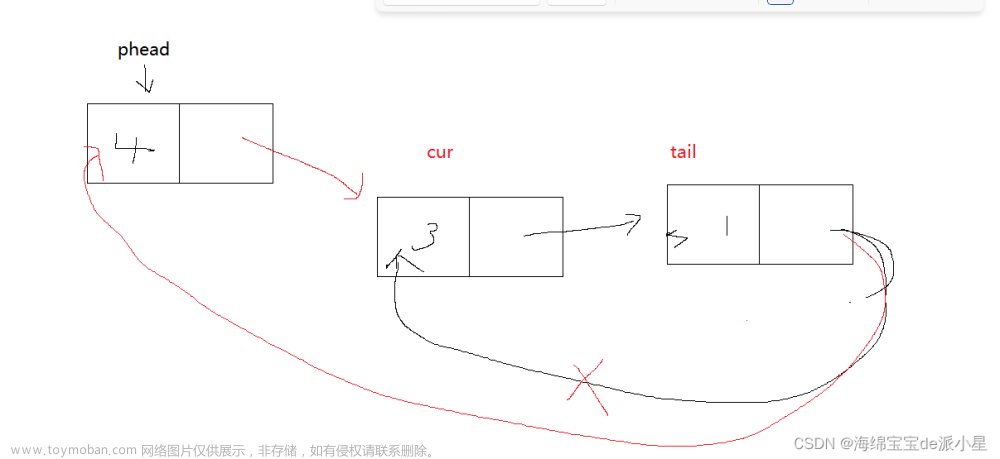
解决约瑟夫环问题的一种常见思路是使用循环链表。首先，我们可以创建一个循环链表，并将人的编号作为节点的值。然后，从第一个节点开始，依次报数，当报数到达 m 时，移除当前节点，继续下一个节点，直到只剩下一个节点为止。

下面是使用 Python 实现约瑟夫环问题的代码：

class Node:
	def __init__(self, value):
		self.value = value
		self.next = None


class CircularLinkedList:
	def __init__(self):
		self.head = None

	def append(self, value):
		new_node = Node(value)
		if not self.head:
			self.head = new_node
			self.head.next = self.head
		else:
			current = self.head
			while current.next != self.head:
				current = current.next
			current.next = new_node
			new_node.next = self.head

	def remove(self, value):
		if not self.head:
			return
		current = self.head
		prev = None
		while True:
			if current.value == value:
				if current == self.head:
					temp = self.head
					while temp.next != self.head:
						temp = temp.next
					temp.next = self.head.next
					self.head = self.head.next
				else:
					prev.next = current.next
				break
			prev = current
			current = current.next
			if current == self.head:
				break

	def get_survivor(self, m):
		current = self.head
		while current.next != current:
			count = 1
			while count != m:
				current = current.next
				count += 1
			self.remove(current.value)
			current = current.next
		return current.value


def josephus(n, m):
	linked_list = CircularLinkedList()
	for i in range(1, n+1):
		linked_list.append(i)
	return linked_list.get_survivor(m)

上述代码中，我们定义了 Node 类表示链表节点，其中包含值 value 和指向下一个节点的指针 next。然后，我们创建了 CircularLinkedList 类来实现循环链表的操作，包括追加节点 append 和移除节点 remove。

在 get_survivor 方法中，我们使用循环链表模拟约瑟夫环的过程。从头节点开始，依次报数，当报数到达 m 时，移除当前节点，并继续下一个节点，直到只剩下一个节点为止。

最后，我们定义了 josephus 函数，它接受人数 n 和报数数字 m 作为输入，创建循环链表并调用 get_survivor 方法来获取最后留下的人的编号。

示例运行

下面是一个使用示例的代码和输出结果：

n = 7
m = 3
survivor = josephus(n, m)
print(f"The survivor's number is: {survivor}")

运行上述代码，将得到以下输出：

The survivor's number is: 4

其它方案

当涉及解决约瑟夫环问题时，除了使用循环链表之外，还存在其他一些解决方案。下面列出了几种常见的解决方案：

1. 数学公式法

约瑟夫环问题的解决可以通过数学公式来推导。假设 n 个人围成一圈，从第一个人开始报数，报到 m 的人出列，然后继续从下一个人开始报数，如此循环，直到所有人都出列。最后留下的人的编号可以通过以下公式计算得出：

f(n, m) = (f(n-1, m) + m) % n

其中，f(n, m) 表示 n 个人中最后留下的人的编号。使用这个公式，我们可以使用递归或循环来计算最后留下的人的编号。

2. 链表法

除了使用循环链表，我们还可以使用普通的链表来解决约瑟夫环问题。首先，我们创建一个链表，将人的编号依次加入到链表中。然后，从链表头部开始，依次报数，当报数到达 m 时，移除当前节点，继续下一个节点，直到只剩下一个节点为止。

3. 数组法

我们可以使用数组来模拟约瑟夫环的过程。首先，创建一个长度为 n 的数组，表示 n 个人的状态。初始化数组的值为 True，表示人还在圈中。然后，从第一个人开始，依次报数，当报数到达 m 时，将对应位置的数组值设为 False，表示该人出列。继续报数，直到只剩下一个人为止。

4. 递推法

通过观察约瑟夫环问题的过程，我们可以发现存在一种递推规律。假设最后留下的人的编号是 f(n, m)，那么当有 n+1 个人时，最后留下的人的编号是 f(n+1, m)。通过观察可以发现，当只剩下一个人时，最后留下的人的编号是 0。利用这种递推规律，我们可以通过循环或递归的方式计算最后留下的人的编号。