【数据结构】数组和字符串（八）：稀疏矩阵的链接存储：十字链表的创建、插入元素、遍历打印（按行、按列、打印矩阵）、销毁-Toy模板网

这篇具有很好参考价值的文章主要介绍了【数据结构】数组和字符串（八）：稀疏矩阵的链接存储：十字链表的创建、插入元素、遍历打印（按行、按列、打印矩阵）、销毁。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

4.2.1 矩阵的数组表示

【数据结构】数组和字符串（一）：矩阵的数组表示

4.2.2 特殊矩阵的压缩存储

矩阵是以按行优先次序将所有矩阵元素存放在一个一维数组中。但是对于特殊矩阵，如对称矩阵、三角矩阵、对角矩阵和稀疏矩阵等, 如果用这种方式存储，会出现大量存储空间存放重复信息或零元素的情况，这样会造成很大的空间浪费。为节约存储空间和算法（程序）运行时间，通常会采用压缩存储的方法。

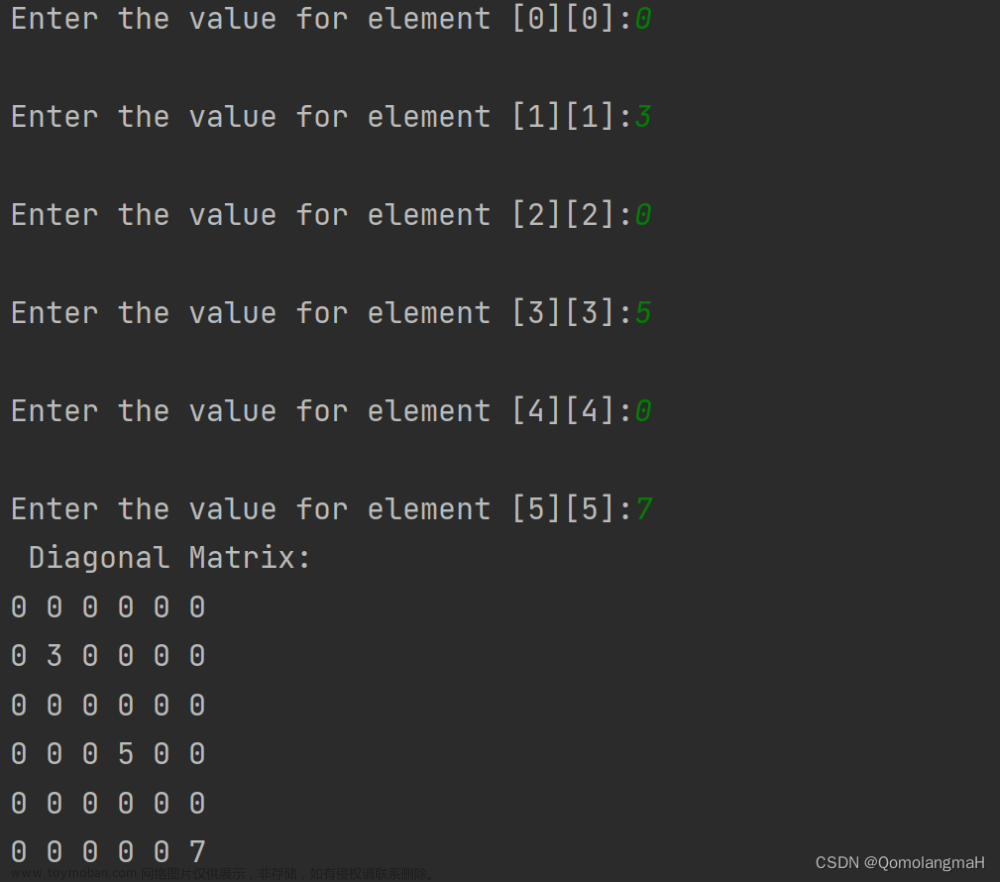
对角矩阵：指除了主对角线以外的元素都为零的矩阵，即对任意 i ≠ j (1≤ i , j ≤n)，都有M(i, j)=0。由于只有主对角线上有非零元素，只需存储主对角线上的元素即可。
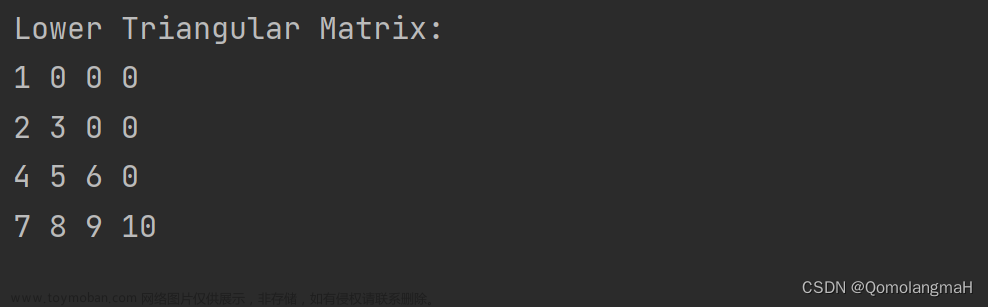
三角矩阵：指上三角或下三角的元素都为零的矩阵。同样地，只需存储其中一部分非零元素，可以节省存储空间。
对称矩阵：指矩阵中的元素关于主对角线对称的矩阵。由于对称矩阵的非零元素有一定的规律，可以只存储其中一部分元素，从而减少存储空间。
稀疏矩阵：指大部分元素为零的矩阵。传统的按行优先次序存储方法会浪费大量空间来存储零元素，因此采用压缩存储的方法更为合适。常见的压缩存储方法有：压缩稠密行（CSR）、压缩稠密列（CSC）、坐标列表（COO）等。

a. 对角矩阵的压缩存储

【数据结构】数组和字符串（二）：特殊矩阵的压缩存储：对角矩阵——一维数组

b~c. 三角、对称矩阵的压缩存储

【数据结构】数组和字符串（三）：特殊矩阵的压缩存储：三角矩阵、对称矩阵——一维数组

d. 稀疏矩阵的压缩存储——三元组表

【数据结构】数组和字符串（四）：特殊矩阵的压缩存储：稀疏矩阵——三元组表

4.2.3三元组表的转置、加法、乘法、操作

【数据结构】数组和字符串（七）：特殊矩阵的压缩存储：三元组表的转置、加法、乘法操作

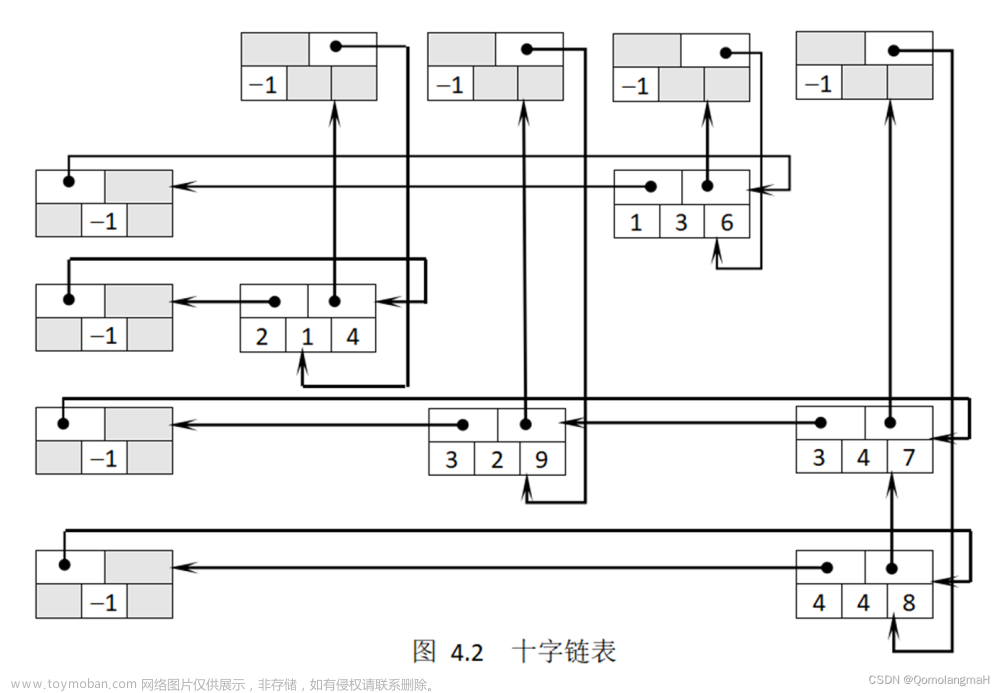
4.2.4十字链表

十字链表（Cross-linked List）是一种用于表示稀疏矩阵的数据结构。稀疏矩阵是指大部分元素为零的矩阵，而十字链表可以有效地存储和操作这种类型的矩阵。在稀疏矩阵的十字链表中，每个非零元素都由一个节点表示。节点包含了几个字段：

LEFT：指向该节点在同一行中的左邻非零元素的地址信息。
UP：指向该节点在同一列中的上邻非零元素的地址信息。
ROW：存储该节点在矩阵中的行号。
COL：存储该节点在矩阵中的列号。
VAL：存储该节点的元素值。

每一行都有一个表头节点，它引导着该行的循环链表，循环链表中的每个节点按照列号的顺序排列。同样，每一列也有一个表头节点，它引导着该列的循环链表，循环链表中的每个节点按照行号的顺序排列。
关于循环链表：【数据结构】线性表（三）循环链表的各种操作（创建、插入、查找、删除、修改、遍历打印、释放内存空间）

【数据结构】数组和字符串（八）：稀疏矩阵的链接存储：十字链表的创建、插入元素、遍历打印（按行、按列、打印矩阵）、销毁,数据结构,数据结构,矩阵,链表,c语言

在稀疏矩阵的十字链表中，每一行和每一列都有一个表头节点。
- 对于行表头节点 BASEROW[i]，其中 i 表示行号，范围从 1 到 m（矩阵的行数）。如果该行为空（即没有非零元素），则 COL(Loc(BASEROW[i])) 的值为 -1。否则，COL(Loc(BASEROW[i])) 的值为该行中最右边的非零元素的列号。
- 对于列表头节点 BASECOL[j]，其中 j 表示列号，范围从 1 到 n（矩阵的列数）。如果该列为空（即没有非零元素），则 ROW(Loc(BASECOL[j])) 的值为 -1。否则，ROW(Loc(BASECOL[j])) 的值为该列中最下边的非零元素的行号。
由于行和列都是循环链表，行表头节点 BASEROW[i] 中的 LEFT 指针循环地链接到该行最右边的非零元素，列表头节点 BASECOL[j] 中的 UP 指针循环地链接到该列最下边的非零元素。

通过这种方式，可以用较少的空间表示稀疏矩阵，并且可以快速地进行行和列的遍历操作。每个节点的 LEFT 和 UP 指针可以用来定位其左邻和上邻非零元素，从而实现矩阵的访问和操作。

0. 十字链表结构

// 定义矩阵节点结构
typedef struct MatrixNode {
    int row;
    int col;
    int value;
    struct MatrixNode* right;
    struct MatrixNode* down;
} MatrixNode;

// 定义稀疏矩阵结构
typedef struct SparseMatrix {
    int rows;
    int cols;
    MatrixNode** rowHeaders;
    MatrixNode** colHeaders;
} SparseMatrix;

left~up ……right~down

1. 创建

SparseMatrix* createSparseMatrix(int rows, int cols) {
    SparseMatrix* matrix = (SparseMatrix*)malloc(sizeof(SparseMatrix));
    matrix->rows = rows;
    matrix->cols = cols;

    // 创建行表头节点数组
    matrix->rowHeaders = (MatrixNode**)malloc((rows + 1) * sizeof(MatrixNode*));
    for (int i = 0; i <= rows; i++) {
        matrix->rowHeaders[i] = NULL;
    }

    // 创建列表头节点数组
    matrix->colHeaders = (MatrixNode**)malloc((cols + 1) * sizeof(MatrixNode*));
    for (int j = 0; j <= cols; j++) {
        matrix->colHeaders[j] = NULL;
    }

    return matrix;
}

分配稀疏矩阵结构体的内存，并将行数和列数存储在结构体的相应字段中。
分配行表头节点数组的内存，并将每个元素初始化为NULL。
分配列表头节点数组的内存，并将每个元素初始化为NULL。
返回指向创建的稀疏矩阵的指针。

2. 销毁

void destroySparseMatrix(SparseMatrix* matrix) {
    if (matrix == NULL) {
        return;
    }

    // 释放所有节点内存
    for (int i = 1; i <= matrix->rows; i++) {
        MatrixNode* current = matrix->rowHeaders[i];
        while (current != NULL) {
            MatrixNode* temp = current;
            current = current->right;
            free(temp);
        }
    }

    // 释放行表头节点数组
    free(matrix->rowHeaders);

    // 释放列表头节点数组
    free(matrix->colHeaders);

    // 释放稀疏矩阵结构
    free(matrix);
}

检查稀疏矩阵指针是否为NULL，如果是，则直接返回。
释放所有节点的内存：
- 遍历每一行，从第一行到最后一行：
  - 通过行表头节点数组获取当前行的行链表头节点。
  - 遍历行链表中的每个节点：
    - 释放当前节点的内存，并将当前节点指针移动到下一个节点。
- 释放行表头节点数组的内存。
- 遍历每一列，从第一列到最后一列：
  - 通过列表头节点数组获取当前列的列链表头节点。
  - 遍历列链表中的每个节点：
    - 释放当前节点的内存，并将当前节点指针移动到下一个节点。
- 释放列表头节点数组的内存。
释放稀疏矩阵结构体的内存。

3. 插入

void insertElement(SparseMatrix* matrix, int row, int col, int value) {
    if (row <= 0 || row > matrix->rows || col <= 0 || col > matrix->cols) {
        printf("Invalid position!\n");
        return;
    }

    // 创建新节点
    MatrixNode* newNode = (MatrixNode*)malloc(sizeof(MatrixNode));
    newNode->row = row;
    newNode->col = col;
    newNode->value = value;
    newNode->right = NULL;
    newNode->down = NULL;

    // 插入到行链表
    if (matrix->rowHeaders[row] == NULL || matrix->rowHeaders[row]->col > col) {
        // 插入到行链表的头部
        newNode->right = matrix->rowHeaders[row];
        matrix->rowHeaders[row] = newNode;
    } else {
        MatrixNode* current = matrix->rowHeaders[row];
        while (current->right != NULL && current->right->col < col) {
            current = current->right;
        }
        newNode->right = current->right;
        current->right = newNode;
    }

    // 插入到列链表
    if (matrix->colHeaders[col] == NULL || matrix->colHeaders[col]->row > row) {
        // 插入到列链表的头部
        newNode->down = matrix->colHeaders[col];
        matrix->colHeaders[col] = newNode;
    } else {
        MatrixNode* current = matrix->colHeaders[col];
        while (current->down != NULL && current->down->row < row) {
            current = current->down;
        }
        newNode->down = current->down;
        current->down = newNode;
    }
}

检查行数和列数是否在有效范围内，如果不是，则打印错误消息并返回。
创建一个新的节点，并将行、列和值存储在节点的相应字段中。
在行链表中插入节点：
- 如果当前行的行链表为空，或者当前行的行链表头节点的列大于要插入的列：
  - 将要插入的节点的右指针指向当前行的行链表头节点。
  - 将当前行的行链表头节点更新为要插入的节点。
- 否则，遍历当前行的行链表，直到找到插入位置：
  - 将要插入的节点的右指针指向当前节点的右指针。
  - 将当前节点的右指针指向要插入的节点。
在列链表中插入节点：
- 如果当前列的列链表为空，或者当前列的列链表头节点的行大于要插入的行：
  - 将要插入的节点的下指针指向当前列的列链表头节点。
  - 将当前列的列链表头节点更新为要插入的节点。
- 否则，遍历当前列的列链表，直到找到插入位置：
  - 将要插入的节点的下指针指向当前节点的下指针。
  - 将当前节点的下指针指向要插入的节点。

4. 打印矩阵形式

void printSparseMatrix(SparseMatrix* matrix) {
    for (int i = 1; i <= matrix->rows; i++) {
        MatrixNode* current = matrix->rowHeaders[i];
        for (int j = 1; j <= matrix->cols; j++) {
            if (current != NULL && current->col == j) {
                printf("%d ", current->value);
                current = current->right;
            } else {
                printf("0 ");
            }
        }
        printf("\n");
    }
}

从第一行开始遍历稀疏矩阵的每一行：
- 通过行表头节点数组获取当前行的行链表头节点。
- 遍历当前行的每一列，从第一列到最后一列：
  - 如果当前节点存在且与当前列匹配，则打印节点的值。
  - 否则，打印0。
- 打印换行符。

5. 按行打印

void printRowNodes(SparseMatrix* matrix) {
    printf("Row Nodes:\n");
    for (int i = 1; i <= matrix->rows; i++) {
        printf("Row %d: ", i);
        MatrixNode* current = matrix->rowHeaders[i];
        while (current != NULL) {
            printf("(%d, %d, %d) ", current->row, current->col, current->value);
            current = current->right;
        }
        printf("\n");
    }
}

从第一行开始遍历稀疏矩阵的每一行：
- 打印当前行的行号。
- 通过行表头节点数组获取当前行的行链表头节点。
- 遍历当前行的行链表，打印每个节点的行、列和值。
- 打印换行符。

6.按列打印

void printColumnNodes(SparseMatrix* matrix) {
    printf("Column Nodes:\n");
    for (int j = 1; j <= matrix->cols; j++) {
        printf("Column %d: ", j);
        MatrixNode* current = matrix->colHeaders[j];
        while (current != NULL) {
            printf("(%d, %d, %d) ", current->row, current->col, current->value);
            current = current->down;
        }
        printf("\n");
    }
}

与行打印等价

7. 主函数

int main() {
    // 创建一个3x3的稀疏矩阵
    SparseMatrix* matrix = createSparseMatrix(3, 3);

    // 插入元素
    insertElement(matrix, 1, 1, 1);
    insertElement(matrix, 1, 2, 2);
    insertElement(matrix, 2, 2, 3);
    insertElement(matrix, 3, 1, 4);
    insertElement(matrix, 3, 3, 5);

    // 打印稀疏矩阵
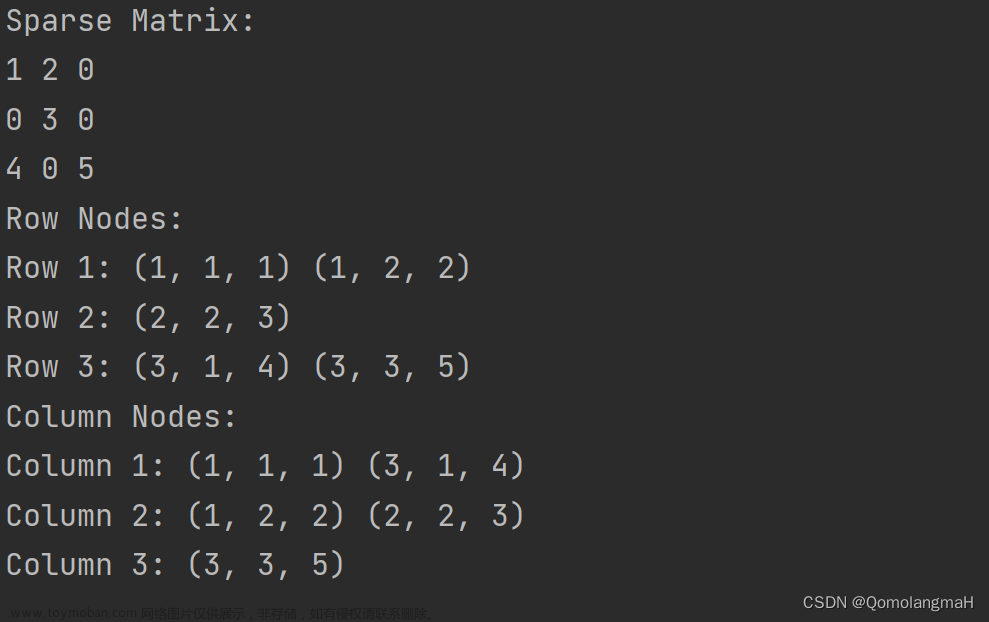
    printf("Sparse Matrix:\n");
    printSparseMatrix(matrix);

    // 输出每行节点
    printRowNodes(matrix);

    // 输出每列节点
    printColumnNodes(matrix);

    // 销毁稀疏矩阵
    destroySparseMatrix(matrix);

    return 0;
}

【数据结构】数组和字符串（八）：稀疏矩阵的链接存储：十字链表的创建、插入元素、遍历打印（按行、按列、打印矩阵）、销毁,数据结构,数据结构,矩阵,链表,c语言文章来源地址https://www.toymoban.com/news/detail-739156.html

8. 代码整合

#include <stdio.h>
#include <stdlib.h>

// 定义矩阵节点结构
typedef struct MatrixNode {
    int row;
    int col;
    int value;
    struct MatrixNode* right;
    struct MatrixNode* down;
} MatrixNode;

// 定义稀疏矩阵结构
typedef struct SparseMatrix {
    int rows;
    int cols;
    MatrixNode** rowHeaders;
    MatrixNode** colHeaders;
} SparseMatrix;

// 创建稀疏矩阵
SparseMatrix* createSparseMatrix(int rows, int cols) {
    SparseMatrix* matrix = (SparseMatrix*)malloc(sizeof(SparseMatrix));
    matrix->rows = rows;
    matrix->cols = cols;

    // 创建行表头节点数组
    matrix->rowHeaders = (MatrixNode**)malloc((rows + 1) * sizeof(MatrixNode*));
    for (int i = 0; i <= rows; i++) {
        matrix->rowHeaders[i] = NULL;
    }

    // 创建列表头节点数组
    matrix->colHeaders = (MatrixNode**)malloc((cols + 1) * sizeof(MatrixNode*));
    for (int j = 0; j <= cols; j++) {
        matrix->colHeaders[j] = NULL;
    }

    return matrix;
}

// 销毁稀疏矩阵
void destroySparseMatrix(SparseMatrix* matrix) {
    if (matrix == NULL) {
        return;
    }

    // 释放所有节点内存
    for (int i = 1; i <= matrix->rows; i++) {
        MatrixNode* current = matrix->rowHeaders[i];
        while (current != NULL) {
            MatrixNode* temp = current;
            current = current->right;
            free(temp);
        }
    }

    // 释放行表头节点数组
    free(matrix->rowHeaders);

    // 释放列表头节点数组
    free(matrix->colHeaders);

    // 释放稀疏矩阵结构
    free(matrix);
}

// 插入元素
void insertElement(SparseMatrix* matrix, int row, int col, int value) {
    if (row <= 0 || row > matrix->rows || col <= 0 || col > matrix->cols) {
        printf("Invalid position!\n");
        return;
    }

    // 创建新节点
    MatrixNode* newNode = (MatrixNode*)malloc(sizeof(MatrixNode));
    newNode->row = row;
    newNode->col = col;
    newNode->value = value;
    newNode->right = NULL;
    newNode->down = NULL;

    // 插入到行链表
    if (matrix->rowHeaders[row] == NULL || matrix->rowHeaders[row]->col > col) {
        // 插入到行链表的头部
        newNode->right = matrix->rowHeaders[row];
        matrix->rowHeaders[row] = newNode;
    } else {
        MatrixNode* current = matrix->rowHeaders[row];
        while (current->right != NULL && current->right->col < col) {
            current = current->right;
        }
        newNode->right = current->right;
        current->right = newNode;
    }

    // 插入到列链表
    if (matrix->colHeaders[col] == NULL || matrix->colHeaders[col]->row > row) {
        // 插入到列链表的头部
        newNode->down = matrix->colHeaders[col];
        matrix->colHeaders[col] = newNode;
    } else {
        MatrixNode* current = matrix->colHeaders[col];
        while (current->down != NULL && current->down->row < row) {
            current = current->down;
        }
        newNode->down = current->down;
        current->down = newNode;
    }
}

// 打印稀疏矩阵
void printSparseMatrix(SparseMatrix* matrix) {
    for (int i = 1; i <= matrix->rows; i++) {
        MatrixNode* current = matrix->rowHeaders[i];
        for (int j = 1; j <= matrix->cols; j++) {
            if (current != NULL && current->col == j) {
                printf("%d ", current->value);
                current = current->right;
            } else {
                printf("0 ");
            }
        }
        printf("\n");
    }
}

// 输出每行节点
void printRowNodes(SparseMatrix* matrix) {
    printf("Row Nodes:\n");
    for (int i = 1; i <= matrix->rows; i++) {
        printf("Row %d: ", i);
        MatrixNode* current = matrix->rowHeaders[i];
        while (current != NULL) {
            printf("(%d, %d, %d) ", current->row, current->col, current->value);
            current = current->right;
        }
        printf("\n");
    }
}

// 输出每列节点
void printColumnNodes(SparseMatrix* matrix) {
    printf("Column Nodes:\n");
    for (int j = 1; j <= matrix->cols; j++) {
        printf("Column %d: ", j);
        MatrixNode* current = matrix->colHeaders[j];
        while (current != NULL) {
            printf("(%d, %d, %d) ", current->row, current->col, current->value);
            current = current->down;
        }
        printf("\n");
    }
}

int main() {
    // 创建一个3x3的稀疏矩阵
    SparseMatrix* matrix = createSparseMatrix(3, 3);

    // 插入元素
    insertElement(matrix, 1, 1, 1);
    insertElement(matrix, 1, 2, 2);
    insertElement(matrix, 2, 2, 3);
    insertElement(matrix, 3, 1, 4);
    insertElement(matrix, 3, 3, 5);

    // 打印稀疏矩阵
    printf("Sparse Matrix:\n");
    printSparseMatrix(matrix);

    // 输出每行节点
    printRowNodes(matrix);

    // 输出每列节点
    printColumnNodes(matrix);

    // 销毁稀疏矩阵
    destroySparseMatrix(matrix);

    return 0;
}