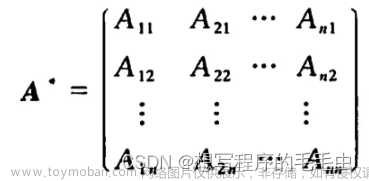
两个实对称矩阵合同的充要条件是它们的正负惯性指数相同。
正惯性指数是矩阵正特征值个数,负惯性指数是矩阵负特征值个数。
即合同矩阵的充分必要条件是特征值的正负号个数相同。
证明:
本论证中的所有矩阵先假设为对称矩阵,但不限于对称矩阵。
根据定义,若矩阵A和矩阵B满足
B
=
P
T
A
P
(1.1)
B = P^T A P \tag{1.1}
B=PTAP(1.1)
则称A与B合同。
根据对称矩阵的性质,可以得出:
A
=
Q
T
Λ
Q
(1.2)
A = Q^T \Lambda Q \tag{1.2}
A=QTΛQ(1.2)
其中, Λ \Lambda Λ既可以是普通的对角矩阵(即标准型),也可以是规范型(即对角元素的绝对值为1)。
将(1.1)带入(1.2)可得:
B = P T Q T Λ Q P = ( Q P ) T Λ ( Q P ) (1.3) B =P^T Q^T \Lambda Q P =(QP) ^T \Lambda (Q P)\tag{1.3} B=PTQTΛQP=(QP)TΛ(QP)(1.3)
假设 ( Q P ) = R (Q P)= R (QP)=R,则(1.3)可化为
B = ( R ) T Λ ( R ) (1.4) B =(R) ^T \Lambda (R)\tag{1.4} B=(R)TΛ(R)(1.4)
假若对角矩阵 Λ \Lambda Λ是标准型,则 Λ \Lambda Λ一定可以利用矩阵乘法化为规范型矩阵。
从(1.2)和(1.4)可以得出,若A和B满足合同条件(1.1),等价于合同矩阵有相同的特征值(规范型),结论得证。
注意:文章来源:https://www.toymoban.com/news/detail-739511.html
- 在对称矩阵中,合同跟相似是等价的,两者能够相互推导。但是在非对称矩阵中,合同和相似是不同的。
- 赫尔韦兹定理证明,可以参考对角线主子式的定义,以及特征值之积等于矩阵的行列式,这两点来证明。从第一阶主子式开始,依次递增的推论出第二个、第三个…第n个特征值的正负号。

还是要感谢万能的知乎。
关于赫尔韦兹定理的证明如下:https://zhuanlan.zhihu.com/p/652751194文章来源地址https://www.toymoban.com/news/detail-739511.html
到了这里,关于合同矩阵充要条件的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!