模拟退火-粒子群全局路径规划+DWA局部路径规划-Toy模板网

这篇具有很好参考价值的文章主要介绍了模拟退火-粒子群全局路径规划+DWA局部路径规划。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

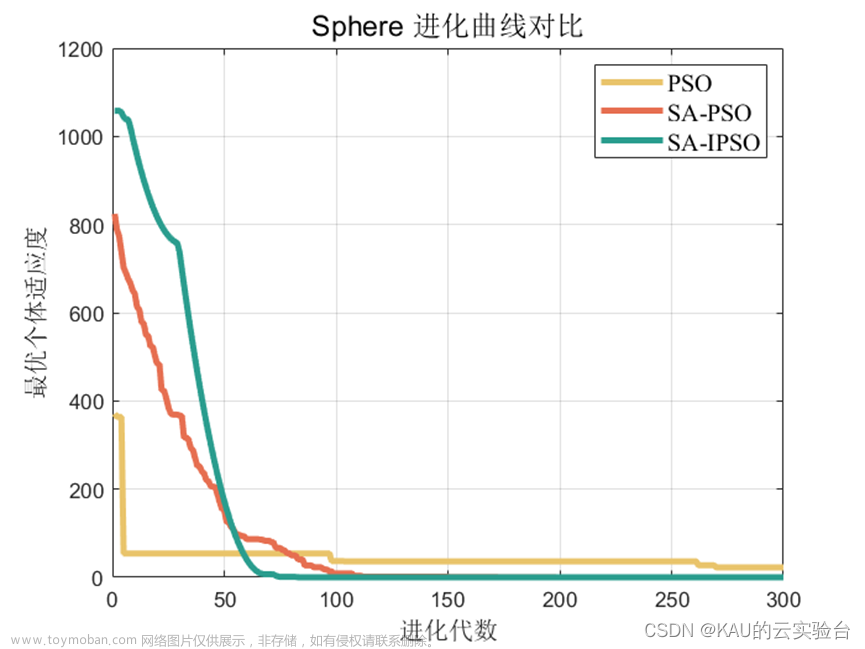
整理了一个路径规划demo，当然图是改进的效果 demo分别有对应的开源可以在网上搜到，我觉得已经介绍的很详细了，所以不做过多的解释，传送门在下面

（写的不好轻喷）

粒子群算法

粒子群本质是参数寻优问题，也就是说在运用到路径规划这块需要对规划的路径进行模型建立，这块的demo当时是从一个b站up那块了解的，我记得好像有个up做了这个的讲解但是我没找到QAQ

模拟退火粒子群,路径规划,动态规划

传送门

b站up的链接：

粒子群算法，路径规划，星际穿越_哔哩哔哩_bilibili

开源的粒子群路径规划demo链接（要感谢上面up的分享）：

Optimal Robot Path Planning using PSO in MATLAB - Yarpiz

（多说一嘴：咱就是说要有点学术态度吧，别直接照搬照抄一点改进都没有，直接拿来用就发论文，看到了真感觉很恶心说的是这篇论文：Verification and Analysis of Two-dimensional Path Planning Objective Function Optimization Based on Classical Particle Swarm Optimization Algorithm）

话说回来，对路径建立数学模型（适应度函数），那么首要的任务是确定要量化哪些信息，demo写在了MyCost.m里面包含两部分：1.路径长度 2.碰撞惩罚

模拟退火粒子群,路径规划,动态规划

在确定了适应度函数之后，就可以用粒子群算法进行寻优了，寻优过程在pso.m中进行。

在初始化时需要确定粒子群的维度n，这个维度可以理解为路径中间节点的个数，节点越多需要迭代的次数也就越多，生成最优路径的可能性也就越大。

%% Problem Definition

model=CreateModel(); %环境初始化 
%@(x) 变量名 = @（输入参数列表）运算表达式 既是一种可用于传参和赋值的变量，又可以作为函数名使用。
%这个x是  第x个粒子群
CostFunction=@(x) MyCost(x,model);  % CostFunction 适应度函数 做了一个声明
nVar=model.n;       % Number of Decision Variables  决策变量数量 10个位置点
VarSize=[1 nVar];   %[1 10] % Size of Decision Variables Matrix  决策变量矩阵的大小

%设置边界
VarMin.x=model.xmin;          
VarMax.x=model.xmax;           
VarMin.y=model.ymin;           
VarMax.y=model.ymax;          

%% PSO Parameters

%迭代次数
MaxIt=500;          % Maximum Number of Iterations  500
%种群规模
nPop=150;           % Population Size (Swarm Size)

%粒子群的三个系数 w为惯性权重系数 c1、c2分别为向个体和群体最优飞行速度
%wdamp的设置是为了降低惯性，提升后期局部搜索能力
w=1;                % Inertia Weight
wdamp=0.98;         % Inertia Weight Damping Ratio
c1=1.5;             % Personal Learning Coefficient
c2=1.5;             % Global Learning Coefficient

%定义速度可行域
alpha=0.1;
VelMax.x=alpha*(VarMax.x-VarMin.x);    % Maximum Velocity
VelMin.x=-VelMax.x;                    % Minimum Velocity
VelMax.y=alpha*(VarMax.y-VarMin.y);    % Maximum Velocity
VelMin.y=-VelMax.y;                    % Minimum Velocity

%% Initialization 种群初始化

% Create Empty Particle Structure
empty_particle.Position=[];
empty_particle.Velocity=[];
empty_particle.Cost=[];
empty_particle.Sol=[];
%结构体里的结构体
empty_particle.Best.Position=[];
empty_particle.Best.Cost=[];
empty_particle.Best.Sol=[];

% Initialize Global Best 因为是找最优（短）距离，所以在一开始置为无穷大
GlobalBest.Cost=inf;
% Create Particles Matrix  创建粒子矩阵 维度（nPop,1）
particle=repmat(empty_particle,nPop,1);

% Initialization Loop
for i=1:nPop
    
    %i = 1的时候 等距离生成10个点 后面的就随机生成
    
    % Initialize Position
    if i > 1  %安排后面那些位置信息
        particle(i).Position=CreateRandomSolution(model);
    else 
        % Straight line from source to destination  从源到目标的直线
        %linspace ==> 在初始点目标点之间等距离生成 n+2(12个点包括初始点和目标点)
        xx = linspace(model.xs, model.xt, model.n+2);  
        yy = linspace(model.ys, model.yt, model.n+2);
        
        %把10个点的信息传给particle
        particle(i).Position.x = xx(2:end-1);
        particle(i).Position.y = yy(2:end-1);
    end
    
    % Initialize Velocity 速度赋0 VarSize=[1,10] zeros(VarSize) ==> zeros(1,10)
    % 相当于返回一个1X10的全零矩阵
    particle(i).Velocity.x=zeros(VarSize);
    particle(i).Velocity.y=zeros(VarSize);
    
    %Evaluation返回路径长度 Cost 和 Sol（拟合点 距离 容忍度 可靠性）
    [particle(i).Cost, particle(i).Sol]=CostFunction(particle(i).Position);
    
    % Update Personal Best  更新个体数据
    particle(i).Best.Position=particle(i).Position;
    particle(i).Best.Cost=particle(i).Cost;
    particle(i).Best.Sol=particle(i).Sol;
    
    % Update Global Best  更新全局数据（选择cost小的值）
    if particle(i).Best.Cost<GlobalBest.Cost
        GlobalBest=particle(i).Best;
    end 
end

% Array to Hold Best Cost Values at Each Iteration  在每次迭代中保持最优值的阵列
BestCost=zeros(MaxIt,1);  %迭代矩阵初始化 每一次的最优值

%% PSO Main Loop 主函数
for it=1:MaxIt（迭代次数）

    for i=1:nPop（粒子个数）

        %x方向
        % 更新速度（粒子群的基本公式）
        particle(i).Velocity.x = w*particle(i).Velocity.x ...
            + c1*rand(VarSize).*(particle(i).Best.Position.x-particle(i).Position.x) ...
            + c2*rand(VarSize).*(GlobalBest.Position.x-particle(i).Position.x);
        
        % Update Velocity Bounds  速度边界约束（如果超过边界 那么等于边界）
        particle(i).Velocity.x = max(particle(i).Velocity.x,VelMin.x);
        particle(i).Velocity.x = min(particle(i).Velocity.x,VelMax.x);
        
        % Update Position 更新位置（上一时刻位置+这这一时刻速度）
        particle(i).Position.x = particle(i).Position.x + particle(i).Velocity.x;
        
        % Velocity Mirroring  速度镜像（我感觉不到这块有啥用）
        OutOfTheRange=(particle(i).Position.x<VarMin.x | particle(i).Position.x>VarMax.x);
        particle(i).Velocity.x(OutOfTheRange)=-particle(i).Velocity.x(OutOfTheRange);
        
        % Update Position Bounds  位置边界约束
        particle(i).Position.x = max(particle(i).Position.x,VarMin.x);
        particle(i).Position.x = min(particle(i).Position.x,VarMax.x);
        
        %y方向（与x方向原理一致）
        % Update Velocity
        particle(i).Velocity.y = w*particle(i).Velocity.y ...
            + c1*rand(VarSize).*(particle(i).Best.Position.y-particle(i).Position.y) ...
            + c2*rand(VarSize).*(GlobalBest.Position.y-particle(i).Position.y);
        
        % Update Velocity Bounds
        particle(i).Velocity.y = max(particle(i).Velocity.y,VelMin.y);
        particle(i).Velocity.y = min(particle(i).Velocity.y,VelMax.y);
        
        % Update Position
        particle(i).Position.y = particle(i).Position.y + particle(i).Velocity.y;
        
        % Velocity Mirroring
        OutOfTheRange=(particle(i).Position.y<VarMin.y | particle(i).Position.y>VarMax.y);
        particle(i).Velocity.y(OutOfTheRange)=-particle(i).Velocity.y(OutOfTheRange);
        
        % Update Position Bounds
        particle(i).Position.y = max(particle(i).Position.y,VarMin.y);
        particle(i).Position.y = min(particle(i).Position.y,VarMax.y);
        

        % Evaluation 评价 循环 返回路径长度Cost和 Sol（拟合点 距离 容忍度 可靠性）
        [particle(i).Cost, particle(i).Sol]=CostFunction(particle(i).Position);
        
        % Update Personal Best  更新个体最优（如果本次迭代cost小，那么记录该粒子的位置、cost、和sol信息）
        if particle(i).Cost<particle(i).Best.Cost
            
            particle(i).Best.Position=particle(i).Position;
            particle(i).Best.Cost=particle(i).Cost;
            particle(i).Best.Sol=particle(i).Sol;
            
            % Update Global Best 更新全局最优（如果本次迭代cost比全局cost要小，那么保留本次cost为全局cost）
            if particle(i).Best.Cost<GlobalBest.Cost
                GlobalBest=particle(i).Best;
            end
        end
    end
    
    % Update Best Cost Ever Found
    BestCost(it)=GlobalBest.Cost; %每次迭代都把种群最优路径加到BestCost中 以便生成适应度曲线
    
    % Inertia Weight Damping
    w=w*wdamp;  %降低惯性 wdamp = 0.98
 
    % Show Iteration Information 显示迭代信息
    if GlobalBest.Sol.IsFeasible
        Flag=' *';
    else
        Flag=[', Violation = ' num2str(GlobalBest.Sol.Violation)];
    end
    disp(['Iteration ' num2str(it) ': Best Cost = ' num2str(BestCost(it)) Flag]);
    
    % Plot Solution
    figure(1);
    PlotSolution(GlobalBest.Sol,model);
    pause(0.01);
    
end

CreateModel.m

function model=CreateModel()

    % Source  初始点
    xs=-50;
    ys=-50;
    
    % Target  目标点
    xt=45;
    yt=36;
    
    %三个障碍物
%     xobs=[1.5 4.0 1.2 40];
%     yobs=[4.5 3.0 1.5 32];
%     robs=[1.5 1.0 0.8 1.2];

    %随机生成100个障碍物
     xobs=(rand(100,1)*2-1)*50; %障碍物x坐标
     yobs=(rand(100,1)*2-1)*50; %障碍物y坐标
     robs=rand(100,1)*3;        %障碍物半径
     for i=1:size(robs)         %约束一下半径都大于1
     if robs(i) < 2
         robs(i) =robs(i)+ 1;     
     end
      
    %10个中间节点
    n=10;   
    
    %位置的可行域范围
    xmin=-50;
    xmax= 50;
    ymin=-50;
    ymax= 50;
    
    %赋值给model结构体
    model.xs=xs;
    model.ys=ys;
    model.xt=xt;
    model.yt=yt;
    model.xobs=xobs;
    model.yobs=yobs;
    model.robs=robs;
    model.n=n;
    model.xmin=xmin;
    model.xmax=xmax;
    model.ymin=ymin;
    model.ymax=ymax;
    
end

ParseSolution.m

function sol2=ParseSolution(sol1,model)

    %把生成的10个点的位置信息传进去
    x=sol1.x;
    y=sol1.y;
    %初始点目标点
    xs=model.xs;
    ys=model.ys;
    xt=model.xt;
    yt=model.yt;
    %障碍物
    xobs=model.xobs;
    yobs=model.yobs;
    robs=model.robs;
    
    XS=[xs x xt];
    YS=[ys y yt];
    k=numel(XS);  %numel 返回 数组元素个数
    TS=linspace(0,1,k); %在 0 - 1 之间等距离生成k个点（包括0 1）
    
    tt=linspace(0,1,100);  %（0,1,5000）的意思是通过样条曲线将tt（5个点）转换成5000个点
    xx=spline(TS,XS,tt);  %spline 三次样条插值 就是说每两个节点之间进行一次三次样条插值，插入的个数是tt（tt越大，生成的轨迹越慢，但也越详细）
    yy=spline(TS,YS,tt);
    
    %前后相邻元素之差 维度降1 用于计算距离
    dx=diff(xx);  
    dy=diff(yy);
    
    L=sum(sqrt(dx.^2+dy.^2)); %计算每一小段距离再求和
    
    nobs = numel(xobs); % Number of Obstacles  numel返回数组元素个数 （几个障碍物）
    Violation = 0;
    for k=1:nobs
        d=sqrt((xx-xobs(k)).^2+(yy-yobs(k)).^2); %计算三次样条插值的 每一个点到第k个障碍物的距离之和
        v=max(1-d/robs(k),0);   %从 1-d/robs(k)或0 中返回最大值 返回0说明d>robs(k) 路径可行  
        Violation=Violation+mean(v); %mean 计算每列的平均值 大于0说明路径与障碍物相遇
    end
    %sol的一些数据
    sol2.TS=TS;
    sol2.XS=XS;
    sol2.YS=YS;
    sol2.tt=tt;
    sol2.xx=xx;
    sol2.yy=yy;
    sol2.dx=dx;
    sol2.dy=dy;
    sol2.L=L;
    sol2.Violation=Violation;
    sol2.IsFeasible=(Violation==0);   %Violation==0 返回 1 sol2.IsFeasible=1 证明可靠
    
    
end

也没啥了吧还有就是障碍物绘制填充什么的，在此基础上在pso中加入模拟退火算法，就形成了模拟退火粒子群算法

模拟退火-粒子群算法：

自适应模拟退火粒子群算法BSAPSO(学习笔记_03)_自适应模拟退火算法_Cloud-Lii的博客-CSDN博客自适应模拟退火粒子群算法BSAPSO（学习笔记_3）https://blog.csdn.net/weixin_49647278/article/details/122549504?utm_medium=distribute.pc_relevant.none-task-blog-2~default~baidujs_baidulandingword~default-1-122549504-blog-127769197.pc_relevant_aa&spm=1001.2101.3001.4242.2&utm_relevant_index=4

DWA算法

DWA算法就是把动态因素考虑进去的，最简单的方法就是在上面的基础上，设置一些动态障碍物，在全局路径规划完成后，进行DWA避障。DWAdemo好像挺久了，这个人写的比较全面，用的也是这个代码，只不过是加到了上面里，所以直接参考他这个自己写一份也是可以的。

DWA算法：

DWA动态窗口法的原理及应用_动态窗口法原理_gophae的博客-CSDN博客看了CSDN博客上面的各种介绍DWA的博客，就这辣鸡点击都能过万？完全是对学术的不尊重吧，还是我来写一下吧。DWA算法的核心：DWA的核心在于所谓的动态窗口，这个东西在sampling based method 中就是sampling. 对于sampling可以是去sample state，也可以sample action. 百度的lattice planner其实就是在sample sta...https://blog.csdn.net/gophae/article/details/105299926

在完成pso后，进行循环迭代DWA算法

%% 机器人的初期状态
x = [-50 -50 pi/4 0 0]'; 
% x下标宏定义 状态[x(m),y(m),yaw(Rad),v(m/s),w(rad/s)]
POSE_X      = 1;  %坐标 X
POSE_Y      = 2;  %坐标 Y
YAW_ANGLE   = 3;  %机器人航向角
V_SPD       = 4;  %机器人速度
W_ANGLE_SPD = 5;  %机器人角速度 
 
goal=[45 36];  %设置目标位置

global dt; 
dt = 0.1;% 时间[s]

%最高速度m/s],最高旋转速度[rad/s],加速度[m/ss],旋转加速度[rad/ss],速度分辨率[m/s],转速分辨率[rad/s]]
Kinematic = [1.5,toRadian(20.0),0.2,toRadian(50.0),0.01,toRadian(1)];

%定义Kinematic的下标含义
MD_MAX_V    = 1;%   最高速度m/s]
MD_MAX_W    = 2;%   最高角速度[rad/s]
MD_ACC      = 3;%   加速度[m/ss]
MD_VW       = 4;%   旋转加速度[rad/ss]
MD_V_RESOLUTION  = 5;%  速度分辨率[m/s]
MD_W_RESOLUTION  = 6;%  转速分辨率[rad/s]]

% 评价函数参数 航向得分的比重、距离得分的比重、速度得分的比重、向前模拟轨迹的时间
evalParam = [0.045, 0.1 ,0.1, 3.0];

% 模拟实验的结果
result_x=[];   %累积存储走过的轨迹点的状态值
tic; % 估算程序运行时间开始
abc = 0;  %循环第abc次

%% 设置纵向移动障碍物
%初始化障碍物的速度参数 在（-1,1）之间
flag_obstacle = [1-2*rand(1) 1-2*rand(1) 1-2*rand(1) 1-2*rand(1) 1-2*rand(1) 1-2*rand(1) 1-2*rand(1) 1-2*rand(1) 1-2*rand(1)];   
vel_obstacle = 0.1;  %障碍物速度参数权值

%设置纵向障碍物的具体目标（9个）
obstacle=[model.xobs(8) model.yobs(8); 
    model.xobs(65) model.yobs(65);
    model.xobs(63) model.yobs(63);
    model.xobs(42) model.yobs(42);
    model.xobs(30) model.yobs(30);
    model.xobs(45) model.yobs(45);
    model.xobs(37) model.yobs(37);
    model.xobs(46) model.yobs(46);
    model.xobs(10) model.yobs(10);];

%% 设置横向移动障碍物
%% 初始化横向移动障碍物速度参数 在（-1,1）之间
flag_obstacle_1 = [1-2*rand(1) 1-2*rand(1) 1-2*rand(1) 1-2*rand(1) 1-2*rand(1) 1-2*rand(1)];   

%设置横向障碍物具体目标（6个）
obstacle_1=[model.xobs(52) model.yobs(52);   
    model.xobs(29) model.yobs(29);
    model.xobs(3) model.yobs(3);
    model.xobs(2) model.yobs(2);
    model.xobs(18) model.yobs(18);
    model.xobs(61) model.yobs(61);];

psi_obs=ones(numel(flag_obstacle),1);
psi_obs_1=ones(numel(flag_obstacle_1),1);

%% 循环
for i = 1:5000
    
    %对obstcle的移动计算
    for j = 1:numel(flag_obstacle)    %移动障碍物设定
        if obstacle(j,2) > 36 && flag_obstacle(j) > 0 || obstacle(j,2) < -50 && flag_obstacle(j) < 0
            flag_obstacle(j) = -flag_obstacle(j);
        end
        obstacle(j,2)=obstacle(j,2)+flag_obstacle(j)*vel_obstacle;   %flag_obstacle(j)*vel_obstacle 变换速度
        %添加obstcle的航向信息
        if flag_obstacle(j)>0
            psi_obs(j,1)=pi/2;
        else
            psi_obs(j,1)=pi*3/2;
        end
    end
    
    model.yobs(8)=obstacle(1,2);
    model.yobs(65)=obstacle(2,2);
    model.yobs(63)=obstacle(3,2);
    model.yobs(42)=obstacle(4,2);
    model.yobs(30)=obstacle(5,2);
    model.yobs(45)=obstacle(6,2);
    model.yobs(37)=obstacle(7,2);
    model.yobs(46)=obstacle(8,2);
    model.yobs(10)=obstacle(9,2);
    
    %对obstcle_1的移动计算
    for j = 1:numel(flag_obstacle_1)    %移动障碍物设定
        if obstacle_1(j,1) > 45 && flag_obstacle_1(j) > 0 || obstacle_1(j,1) < -50 && flag_obstacle_1(j) < 0
            flag_obstacle_1(j) = -flag_obstacle_1(j);
        end
        obstacle_1(j,1)=obstacle_1(j,1)+flag_obstacle_1(j)*vel_obstacle;   %flag_obstacle(j)*vel_obstacle 变换速度
        %添加obstacle_1的航向信息
        if flag_obstacle_1(j)>0
            psi_obs_1(j,1)=0;
        else
            psi_obs_1(j,1)=pi;
        end
    end
    
    model.xobs(52)=obstacle_1(1,1);
    model.xobs(29)=obstacle_1(2,1);
    model.xobs(3)=obstacle_1(3,1);
    model.xobs(2)=obstacle_1(4,1);
    model.xobs(18)=obstacle_1(5,1);
    model.xobs(61)=obstacle_1(6,1);
    
    %撞上纵向移动障碍物
    for l = 1:numel(flag_obstacle)
        if norm(obstacle(l,:)-x(1:2)')-1 < 0
            disp('==========Hit an obstacle!!==========');  %撞上障碍物
            temp = 1;
            break;
        end
    end
    %撞上横向移动障碍物
    for l = 1:numel(flag_obstacle_1)
        if norm(obstacle_1(l,:)-x(1:2)')-1 < 0
            disp('==========Hit an obstacle!!!==========');  %撞上障碍物
            temp = 1;
            break;
        end
    end
    if temp == 1
        break;
    end
    
    % DWA参数输入 返回控制量 u = [v(m/s),w(rad/s)] 和 轨迹
    [u,traj] = DynamicWindowApproach(x,Kinematic,goal(k,:),evalParam,model,psi_obs,psi_obs_1,obstacle,obstacle_1);%算出下发速度u/当前速度u
    x = f(x,u);% 机器人移动到下一个时刻的状态量 根据当前速度和角速度推导 下一刻的位置和角度
    abc = abc+1;
    % 历史轨迹的保存
    result_x = [result_x; x'];  %最新结果 以行的形式 添加到result.x， 保存的是所有状态参数值，包括坐标xy、朝向、线速度、角速度，其实应该是只取坐标就OK
    
    % 是否到达目的地
    if norm(x(POSE_X:POSE_Y)-goal(k,:)')<2   % norm函数来求得坐标上的两个点之间的距离
        disp('==========Arrive Goal!!==========');break;
    end
    
    
    %导入PlotSolution_2绘制 动态障碍物  +  机器人模型
    ArrowLength = 0.5;      % 箭头长度
    PlotSolution_2(traj,result_x,x,ArrowLength,GlobalBest.Sol,model);
    
    disp(['time ' num2str(i)]); %打印
end
 
 
%% 航行时间   形式：时间已过 ** 秒。
toc;  

%% 计算航迹总长度
lx_c=[-50;result_x(:,1);45];
ly_c=[-50;result_x(:,2);36];

dlx=diff(lx_c);
dly=diff(ly_c);

L_c=sum(sqrt(dlx.^2+dly.^2));

disp(['DWA航迹长度为： ' num2str(L_c)]); %打印

DynamicWindowApproach.m

function [u,trajDB] = DynamicWindowApproach(x,model,goal,evalParam,model_1,psi_obs,psi_obs_1,obstacle,obstacle_1)
% Dynamic Window [vmin,vmax,wmin,wmax] 最小速度 最大速度 最小角速度 最大角速度速度
Vr = CalcDynamicWindow(x,model);  % 根据当前状态 和 运动模型 计算当前的参数允许范围（最小速度 最大速度 最小角速度 最大角速度速度）

% 评价函数的计算 evalDB N*5  每行一组可用参数 分别为 速度、角速度、航向得分、距离得分、速度得分
%               trajDB      每5行一条轨迹 每条轨迹都有状态x点串组成
[evalDB,trajDB]= Evaluation(x,Vr,goal,model_1,model,evalParam,psi_obs,psi_obs_1,obstacle,obstacle_1);  %evalParam 评价函数参数 [heading,dist,velocity,predictDT]

if isempty(evalDB)
    disp('no path to goal!!');
    u=[0;0];return;
end

% 各评价函数正则化
evalDB = NormalizeEval(evalDB);

% 最终评价函数的计算
feval=[];
for id=1:length(evalDB(:,1))
    feval = [feval;evalParam(1:3)*evalDB(id,3:5)']; %根据评价函数参数 前三个参数分配的权重 计算每一组可用的路径参数信息的得分  评价参数前三个指标 航向得分比重、距离得分比重、速度得分比重 X evalDB的 第三个到第五个指标 航向、距离、速度
end
evalDB = [evalDB feval]; % 最后一组；加最后一列，每一组速度的最终得分

[maxv,ind] = max(feval);% 选取评分最高的参数 对应分数返回给 maxv  对应下标返回给 ind
u = evalDB(ind,1:2)';% 返回最优参数的速度、角速度
end

Evaluation.m(这块把接口写上了以便后续为所欲为包括障碍物角度以及障碍物位置)

function [evalDB,trajDB] = Evaluation(x,Vr,goal,model_1,model,evalParam,psi_obs,psi_obs_1,obstacle,obstacle_1)
evalDB = [];
trajDB = [];
for vt = Vr(1):model(5):Vr(2)       %根据速度分辨率遍历所有可用速度： 最小速度和最大速度 之间 速度分辨率 递增
    for ot=Vr(3):model(6):Vr(4)     %根据角度分辨率遍历所有可用角速度： 最小角速度和最大角速度 之间 角度分辨率 递增
        % 轨迹推测; 得到 xt: 机器人向前运动后的预测位姿; traj: 当前时刻 到 预测时刻之间的轨迹（由轨迹点组成）
        [xt,traj] = GenerateTrajectory(x,vt,ot,evalParam(4));  %evalParam(4),前向模拟时间;  得到运动后的位姿 + 这段路径
        % 各评价函数的计算
        heading = CalcHeadingEval(xt,goal); % 前项预测终点的航向得分  偏差越小分数越高
        [dist,Flag] = CalcDistEval(xt,model_1);    % 前项预测终点 距离最近障碍物的间隙得分 距离越远分数越高
        vel = abs(vt);                  % 速度得分 速度越快分越高
        stopDist = CalcBreakingDist(vel,model); % 制动距离的计算
         if dist > stopDist && Flag == 0 % 如果可能撞到最近的障碍物 则舍弃此路径 （到最近障碍物的距离 大于 刹车距离 才取用）
%         if Flag == 0 % 如果可能撞到最近的障碍物 则舍弃此路径 （到最近障碍物的距离 大于 刹车距离 才取用）
            evalDB = [evalDB;[vt ot heading dist vel]];
            trajDB = [trajDB;traj];   % 每5行 一条轨迹
        end
    end
end
end

其他内容基本就跟上面博主写的一样了，算法很简单，一看就懂

这块说一下障碍物移动，也是参考了DWA算法的demo

在PSO随机生成障碍物的基础上，将障碍物信息保存到Excel中，然后读取的Excel数据，以便更改具体障碍物，障碍物的迭代移动demo在PlotSolution_2.m中

function PlotSolution_2(traj,result_x,x,ArrowLength,sol,model)

    xs=model.xs;
    ys=model.ys;
    xt=model.xt;
    yt=model.yt;
    xobs=model.xobs;
    yobs=model.yobs;
    robs=model.robs;
    
    XS=sol.XS;
    YS=sol.YS;
    xx=sol.xx;
    yy=sol.yy;
    
    theta=linspace(0,2*pi,100);
    for k=1:numel(xobs)   %填充障碍物（应该是）
        fill(xobs(k)+robs(k)*cos(theta),yobs(k)+robs(k)*sin(theta),[0.5 0.7 0.8]);
        hold on;
    end
    
  
    fill(xobs(8)+robs(8)*cos(theta),yobs(8)+robs(8)*sin(theta),[0.9373 0.4353 0.4235]);
    hold on;
    fill(xobs(65)+robs(65)*cos(theta),yobs(65)+robs(65)*sin(theta),[0.9373 0.4353 0.4235]);
    hold on;
    fill(xobs(63)+robs(63)*cos(theta),yobs(63)+robs(63)*sin(theta),[0.9373 0.4353 0.4235]);
    hold on;
    fill(xobs(42)+robs(42)*cos(theta),yobs(42)+robs(42)*sin(theta),[0.9373 0.4353 0.4235]);
    hold on;
    fill(xobs(30)+robs(30)*cos(theta),yobs(30)+robs(30)*sin(theta),[0.9373 0.4353 0.4235]);
    hold on;
    fill(xobs(45)+robs(45)*cos(theta),yobs(45)+robs(45)*sin(theta),[0.9373 0.4353 0.4235]);
    hold on;
    fill(xobs(37)+robs(37)*cos(theta),yobs(37)+robs(37)*sin(theta),[0.9373 0.4353 0.4235]);
    hold on;
    fill(xobs(46)+robs(46)*cos(theta),yobs(46)+robs(46)*sin(theta),[0.9373 0.4353 0.4235]);
    hold on;
    fill(xobs(10)+robs(10)*cos(theta),yobs(10)+robs(10)*sin(theta),[0.9373 0.4353 0.4235]);
    hold on;

    
    fill(xobs(52)+robs(52)*cos(theta),yobs(52)+robs(52)*sin(theta),[0.9294, 0.6941, 0.5137]);
    hold on;
    fill(xobs(29)+robs(29)*cos(theta),yobs(29)+robs(29)*sin(theta),[0.9294, 0.6941, 0.5137]);
    hold on;
    fill(xobs(3)+robs(3)*cos(theta),yobs(3)+robs(3)*sin(theta),[0.9294, 0.6941, 0.5137]);
    hold on;
    fill(xobs(2)+robs(2)*cos(theta),yobs(2)+robs(2)*sin(theta),[0.9294, 0.6941, 0.5137]);
    hold on;
    fill(xobs(18)+robs(18)*cos(theta),yobs(18)+robs(18)*sin(theta),[0.9294, 0.6941, 0.5137]);
    hold on;
    fill(xobs(61)+robs(61)*cos(theta),yobs(61)+robs(61)*sin(theta),[0.9294, 0.6941, 0.5137]);
    hold on;
    
    
    POSE_X=x(1);
    POSE_Y=x(2);
    YAW_ANGLE=x(3);
    V_SPD=x(4);
    W_ANGLE_SPD=x(5);
    
    n=0.02;
    long = 150;  %船长
    width = 50;  %船宽
    l = n*long;  %n是比例
    w = n*width;
    % psi = psi*pi/180;
    YAW_ANGLE_1 = YAW_ANGLE ;

    y1 = POSE_X - (l/2)*cos(YAW_ANGLE_1);%1
    x1 = POSE_Y - (l/2)*sin(YAW_ANGLE_1);
    y2 = POSE_X + (l/6)*cos(YAW_ANGLE_1);%2
    x2 = POSE_Y + (l/6)*sin(YAW_ANGLE_1);
    y3 = POSE_X + (l/2)*cos(YAW_ANGLE_1);%3
    x3 = POSE_Y + (l/2)*sin(YAW_ANGLE_1);
    y5 = y1 - (w/2)*sin(YAW_ANGLE_1);%5
    x5 = x1 + (w/2)*cos(YAW_ANGLE_1);
    y6 = y1 + (w/2)*sin(YAW_ANGLE_1);%6
    x6 = x1 - (w/2)*cos(YAW_ANGLE_1);
    y4 = y2 - (w/2)*sin(YAW_ANGLE_1);%4
    x4 = x2 + (w/2)*cos(YAW_ANGLE_1);
    y7 = y2 + (w/2)*sin(YAW_ANGLE_1);%7
    x7 = x2 - (w/2)*cos(YAW_ANGLE_1);


    
    x = [x3 x4 x5 x6 x7 x3];
    y = [y3 y4 y5 y6 y7 y3];
    
    plot(y,x,'g','LineWidth',0.5);  %画船
    quiver(POSE_X, POSE_Y, ArrowLength*cos(YAW_ANGLE), ArrowLength*sin(YAW_ANGLE),'ok'); %画圆
    
    % 绘制走过的所有位置 所有历史数据的 X、Y坐标
    plot(result_x(:,1),result_x(:,2),'-b');
    
    % 探索轨迹 画出待评价的轨迹
    if ~isempty(traj) %轨迹非空
        for it=1:length(traj(:,1))/5    %计算所有轨迹数  traj 每5行数据 表示一条轨迹点
            ind = 1+(it-1)*5; %第 it 条轨迹对应在traj中的下标
            plot(traj(ind,:),traj(ind+1,:),'-g'); hold on;  %根据一条轨迹的点串画出轨迹   traj(ind,:) 表示第ind条轨迹的所有x坐标值  traj(ind+1,:)表示第ind条轨迹的所有y坐标值
        end
    end
    
    
    plot(xx,yy,'k','LineWidth',2);
    plot(XS,YS,'ro');
    plot(xt,yt,'kp','MarkerSize',16,'MarkerFaceColor','g');  %终点
    hold off;
    grid on;
    axis equal;
    drawnow limitrate;

end

整体demo打包到一起发吧，在此再次感谢前面几个博主的分享

代码传送门：

https://download.csdn.net/download/weixin_53293018/87679985?spm=1001.2014.3001.5503

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/weixin_53293018/article/details/129802545
文章来源地址https://www.toymoban.com/news/detail-739616.html

到了这里，关于模拟退火-粒子群全局路径规划+DWA局部路径规划的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！