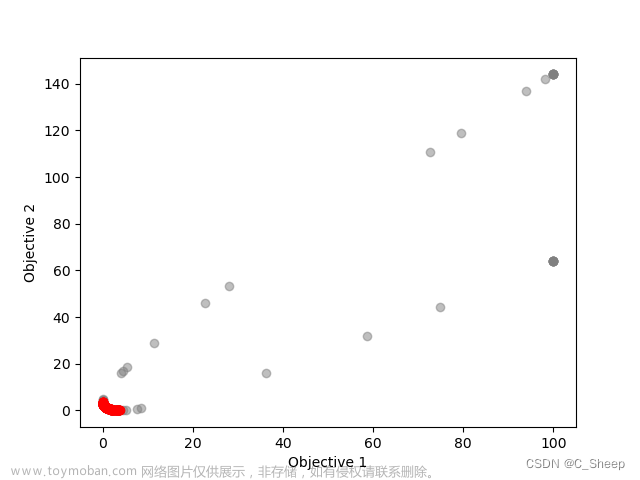
下面我们使用遗传算法尝试求解一元函数的最值
y
=
s
i
n
(
x
2
−
1
)
+
2
c
o
s
(
2
x
)
,
x
∈
[
0
,
10
]
y=sin(x^2-1)+2cos(2x),x\in [0,10]
y=sin(x2−1)+2cos(2x),x∈[0,10]
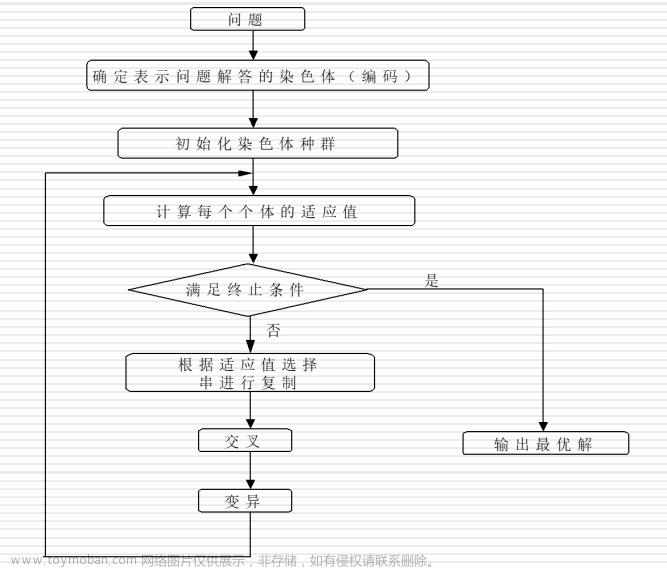
遗传算法求解过程
算法参数
# 种群数量
m_population = 50
# 迭代次数(种群进化代数)
epoch = 99
# 基因个数
L = 40
# 交叉概率
mp = 0.5
# 变异概率
mm = 0.01
# 最大函数值
mf = 0
# 最大函数值对应的自变量
mx = 0
# 变量约束
bound = [0, 10]
# 存储每一代的最优个体
f_list = []
x_list = []
构建初始化种群
生成二进制数组,形状为(种群个体数,个体基因个数),即(m_population, L)
population = np.random.randint(0, 2, (m_population, L))
运行结果
解码(二进制>十进制)
- 将生成的二进制数组先转换为十进制数字,便于计算个体适应度
二进制转十进制有多种方法,这里笔者提供一种:由于个体基因是以二进制数组的形式存在,我们先将二进制数组转换为二进制字符串,然后使用int()函数实现转换过程
for i in range(m_population):
transform_middle = int(''.join(map(lambda x: str(x), population[i])), 2)
- 然后进行标准化。由于二进制字符串的长度为40,转化得到的十进制数字将会非常大,我们的自变量约束区域为 b o u n d = [ 0 , 10 ] bound=[0,10] bound=[0,10],我们将得到的十进制数字都转化到 0 − 10 0-10 0−10之间,
transform_[i] = bound[0] + (bound[1] - bound[0]) * transform_middle / pow(2, L)
- 求不同个体的的适应度
f = fun(transform_)
自然选择
这是事关重要的一步,我们知道适应度大的个体有更大的概率存活下来,如何使用代码实现这一过程?
我们使用频数来代替概率,在原来种群的基础之上,我们通过概率选择一些个体出来,数量等于原来的种群个体数量相等,这样选择出来的个体在组成一个新的种群,这样我们便完成了自然选择这一过程
bingo = np.random.choice(np.arange(m_population), m_population, True, f / sum(f))
select_populaton = population[bingo]
# 生成目前种群的两个复制版本,实际上不生成也行,但是这样有利于模拟两个体的交配过程
last_gen = select_populaton
new_gen = select_populaton.copy()
交叉
交叉相当于两个个体(染色体)交配。遗传算法中有多种方式实现交叉,笔者在这里采用一种叫做单点交叉的方式
match = np.random.choice(np.arange(m_population), m_population, False)
for i in range(m_population // 2):# 种群中的个体两两结合
if np.random.rand() < mp:# 以交叉概率
location = np.random.randint(0, L)# 交叉点
last_gen[match[i]][:location], new_gen[match[L - i - 1]][:location] = \
new_gen[match[L - i - 1]][:location], last_gen[match[i]][:location]
变异
for i in range(m_population):
for j in range(L):
if np.random.rand() < mm:
new_gen[i][j] = 1 if new_gen[i][j]==0 else 0
此时上一代繁衍基本结束,new_gen即为新一代种群
将population更新为新种群
population = new_gen
解码(新种群>十进制)
transform_1 = np.zeros(m_population)
for i in range(m_population):
transform_middle = int(''.join(map(lambda x: str(x), new_gen[i])), 2)
transform_1[i] = bound[0] + (bound[1] - bound[0]) * transform_middle / pow(2, L)
计算新种群的适应度
# 计算适应度
new_f = fun(transform_1) - 4
# 选择出最优的个体
mx = transform_1[np.argmax(new_f)]
# 最优适应度
mf = new_f.max()
# 将每一代最优个体及其适应度添加到数组中便于统计
f_list.append(mf)
x_list.append(mx)
运行结果

完整代码及其可视化版本
可视化,即使用matplotlib库动态绘制遗传算法求解该问题的过程,主要添加的代码如下
- 绘制该函数图像
- 以散点图的形式绘制每一代个体的最优个体及其适应度
import numpy as np
import matplotlib.pyplot as plt
# 定义适应度函数
def fun(x):
return np.sin(x ** 2 - 1) + 2 * np.cos(2 * x) + 4
plt.ion()
inputs=np.arange(0,10,0.1)
output=[fun(i)-4 for i in inputs]
plt.plot(inputs,output)
# 种群数量
m_population = 50
# 迭代次数
epoch = 99
# 基因个数
L = 40
# 交叉概率
mp = 0.5
# 变异概率
mm = 0.01
# 最大函数值
mf = 0
# 最大函数值对应的自变量
mx = 0
bound = [0, 10]
f_list = []
x_list = []
# 生成二进制种群
population = np.random.randint(0, 2, (m_population, L))
transform_ = np.zeros(m_population)
# 二进制>十进制,并标准化
for i in range(m_population):
transform_middle = int(''.join(map(lambda x: str(x), population[i])), 2)
transform_[i] = bound[0] + (bound[1] - bound[0]) * transform_middle / pow(2, L)
# 计算当前种群适应度
f = fun(transform_)
for num in range(epoch):
# 自然选择
bingo = np.random.choice(np.arange(m_population), m_population, True, f / sum(f))
select_populaton = population[bingo]
# 生成目前种群的两个复制版本,实际上不生成也行,但是这样有利于模拟两个体的交配过程
last_gen = select_populaton
new_gen = select_populaton.copy()
# 交叉
match = np.random.choice(np.arange(m_population), m_population, False)
for i in range(m_population // 2):
if np.random.rand() < mp:
location = np.random.randint(0, L)
last_gen[match[i]][:location], new_gen[match[L - i - 1]][:location] = \
new_gen[match[L - i - 1]][:location], last_gen[match[i]][:location]
# 变异
for i in range(m_population):
for j in range(L):
if np.random.rand() < mm:
new_gen[i][j] = 1 - new_gen[i][j]
# 现在new_gen就是新生成的种群,我们需要将其转化为十进制
# 我们先生成一个空数组,然后使用它储存转化后的种群十进制
transform_1 = np.zeros(m_population)
for i in range(m_population):
transform_middle = int(''.join(map(lambda x: str(x), new_gen[i])), 2)
transform_1[i] = bound[0] + (bound[1] - bound[0]) * transform_middle / pow(2, L)
# 计算适应度
new_f = fun(transform_1) - 4
# 选择出最优的个体
mx = transform_1[np.argmax(new_f)]
# 将当前的种群视为最优的种群
population = new_gen
# 最优适应度
mf = new_f.max()
f_list.append(mf)
x_list.append(mx)
plt.scatter(mx,mf)
plt.title(f'epoch:{num+1}')
plt.pause(0.1)
plt.ioff()
plt.show()
print(max(x_list), max(f_list))
>>> 9.93222096441059 2.9685353661257627
运行结果
其他
numpy中的随机数
- np.random.randint
numpy.random.randint(low, high=None, size=None, dtype=int)
返回 ( l o w , h i g h ] (low,high] (low,high]之间的随机整数或形状为size的随机整数数组文章来源:https://www.toymoban.com/news/detail-739798.html
- np.random.choice
numpy.random.choice(a, size=None, replace=True, p=None)
从一维数组a中抽取随机样本文章来源地址https://www.toymoban.com/news/detail-739798.html
| 参数 | 描述 | |
|---|---|---|
| size | int or tuple of ints, optional | 随机样本的数组形状 |
| replace | boolean, optional | 表示样本是否可以重复出现 |
| p | 1-D array-like, optional | 每个样本被抽取到的概率 |
到了这里,关于python遗传算法(应用篇1)--求解一元函数极值的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!