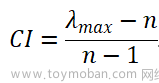清风学习笔记—层次分析法—matlab对判断矩阵的一致性检验-Toy模板网

这篇具有很好参考价值的文章主要介绍了清风学习笔记—层次分析法—matlab对判断矩阵的一致性检验。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

在判断矩阵是否为正互反矩阵这块，我写了两种代码，改进前很麻烦且有错误，改进后简洁多了，改进前的代码还有错误，忽略了对角线的值必须都是1，只考虑了除开对角线的元素相乘为1。


%% 改进前代码
A=[3 2 4;1/2 4 2;1/4 1/2 5]
diag_A=diag(A)
C=ones(1,size(A,2))
%将矩阵A的对角线更改为全1向量C
A(logical(eye(size(A))))=C
%获取矩阵A的共轭转置矩阵A2
A2=A.'
%如果A2和A进行点乘能够得到一个单位矩阵，那么A就是一个正互反矩阵
if isequal(A2.*A,ones(size(A,1)))
    fprintf("A是一个正互反矩阵")
end
%将矩阵A的主对角线进行还原
A(logical(eye(size(A))))=diag_A

%% 改进后代码
if sum(sum(A'.*A~=ones(n)))>0
    error=3;
    disp("不为正互反矩阵")
end

下面是全部代码文章来源地址https://www.toymoban.com/news/detail-740101.html

%% 输入判断矩阵
clear;clc
disp('请输入判断矩阵A： ')
A = input('判断矩阵A=');
[r,c]=size(A);
error=0;
%% 判断矩阵是否为方阵并且阶数大于等于2
if r~=c || r<2
  error=1;
end
%% 判断矩阵是否大于15
if r==c&&r>15
    error=2;
end

%% 判断矩阵A是否为正互反矩阵
if error~=1 && sum(sum(A'.*A~=ones(r)))>0
    error=3;
end
%% 计算
if error==0
    %% 算术平均法求权重
    Sum_A = sum(A);
    [n,m] = size(A);
    SUM_A = repmat(Sum_A,n,1);
    Stand_A = A ./ SUM_A;
    sum(Stand_A,2);
    disp('算术平均法求权重的结果为：');
    disp(sum(Stand_A,2) ./ n)
    %% 方法2：几何平均法求权重
    Prduct_A = prod(A,2);
    Prduct_n_A = Prduct_A .^ (1/n);
    disp('几何平均法求权重的结果为：');
    disp(Prduct_n_A ./ sum(Prduct_n_A));
    %% 方法3：特征值法求权重

    [V,D] = eig(A);
    Max_eig = max(max(D));
    [r,c] = find(D == Max_eig , 1);
    V(:,c);
    disp('特征值法求权重的结果为：');
    disp( V(:,c) ./ sum(V(:,c)) )
    %% 计算一致性比例CR
    CI = (Max_eig - n) / (n-1);
    RI=[0 0 0.52 0.89 1.12 1.26 1.36 1.41 1.46 1.49 1.52 1.54 1.56 1.58 1.59];  %注意哦，这里的RI最多支持 n = 15
    CR=CI/RI(n);
    disp('一致性指标CI=');disp(CI);
    disp('一致性比例CR=');disp(CR);
    if CR<0.10
        disp('因为CR < 0.10，所以该判断矩阵A的一致性可以接受!');
    else
        disp('注意：CR >= 0.10，因此该判断矩阵A需要进行修改!');
    end
elseif error==1
        disp("输入的A不为方阵或者阶数小于2")
elseif error==2
        disp("判断矩阵的阶数大于15")
elseif error==3
    disp("不为正互反矩阵")
end

到了这里，关于清风学习笔记—层次分析法—matlab对判断矩阵的一致性检验的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！