稀疏矩阵（表示、转置）-Toy模板网

这篇具有很好参考价值的文章主要介绍了稀疏矩阵（表示、转置）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

一、稀疏矩阵的三元组表示法

1.1 稀疏矩阵非零元素的三元组存储表示

1.2 稀疏矩阵三元组表的类型定义

二、用三元组实现稀疏矩阵的转置运算

2.1 方法一：列序递增转置法

2.1.1 算法思想

2.1.2 算法实现

2.2 方法二：一次定位快速转置法

2.2.1 算法思想

2.2.2 算法实现

一、稀疏矩阵的三元组表示法

1.1 稀疏矩阵非零元素的三元组存储表示

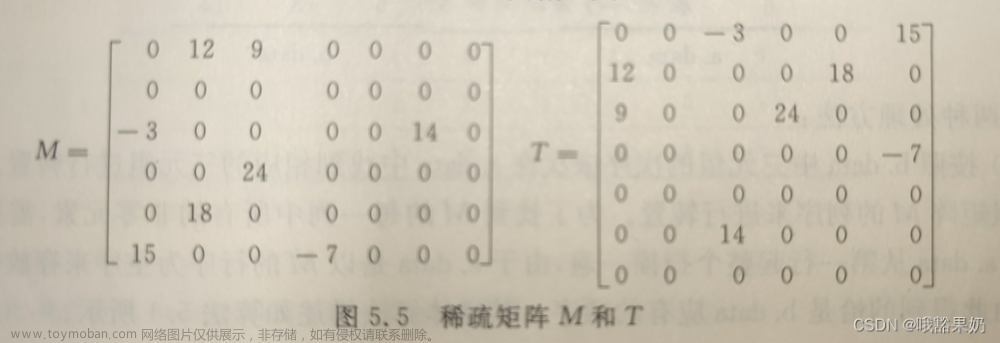
对于稀疏矩阵的压缩存储，采取只存储非零元素的方法。

由于稀疏矩阵中非零元素的分布没有规律，因此在存储非零元素值的同时，还必须存储该非零元素在矩阵中所处的行号和列号的位置信息，即按三元组的结构存储。

如图所示：

稀疏矩阵a(n行m列,非零元素数为t)采用三元组b表示,那么在三元组中访问a[i][j]所需,数据结构——用C语言描述,矩阵,算法,数据结构,c语言

为处理方便，将稀疏矩阵中的非零元素对应的三元组按行序为主序的一维结构数组进行存储，即将矩阵每一行（行有小到大）的全部非零元素的三元组按列号递增存储。

如图所示：

稀疏矩阵a(n行m列,非零元素数为t)采用三元组b表示,那么在三元组中访问a[i][j]所需,数据结构——用C语言描述,矩阵,算法,数据结构,c语言

1.2 稀疏矩阵三元组表的类型定义

#define MAXSIZE 1000
#define ElementType int

/* 定义三元组的类型 */
typedef struct {
    ElementType e;   /* 该非零元素的值 */
    int row, col;    /* 该非零元素的行值和列值*/
} Triple;

/* 定义稀疏矩阵的类型 */
typedef struct {
    Triple data[MAXSIZE + 1];   /* 非零元素的三元组表，其中data[0]被弃用 */
    int m, n, len;              /* 稀疏矩阵的行数、列数以及非零元素的个数 */
} TSMatrix;

二、用三元组实现稀疏矩阵的转置运算

2.1 方法一：列序递增转置法

2.1.1 算法思想

算法思想：按照被转置矩阵三元组表A的列序递增的顺序进行转置，并依次送入转置后矩阵的三元组表B中。这样一来，转置后矩阵的三元组表B恰好是以行序为主序。

如图所示：

2.1.2 算法实现

void TransposeTSMatrix(TSMatrix *from, TSMatrix *to) {
    int i, j, k;

    /* 交换基本数据 */
    to->m = from->n;
    to->n = from->m;
    to->len = from->len;

    if (to->len == 0)
        return;

    j = 1;
    for (k = 1; k <= from->n; ++k)
    /* 扫描三元组表from共from->n次，每次寻找列值为k的三元组进行转置 */
        for (i = 1; i <= from->len; ++i)
        /* 从头到尾扫描三元组表from，寻找行值为k的三元组进行转置 */
            if (from->data[i].col == k) {
                to->data[j].row = from->data[i].col;
                to->data[j].col = from->data[i].row;
                to->data[j].e = from->data[i].e;
                ++j; /* j加1，指向下一个转置后元素的位置下标 */
            }
}

2.2 方法二：一次定位快速转置法

2.2.1 算法思想

为了能将被转置三元组表from中的元素一次定位到三元组表to的正确位置上，需要预先计算以下数据：

1、待转置矩阵三元组表from每一列非零元素的总个数；

2、待转置矩阵每一列中第一个非零元素在三元组表to中的正确位置。

为此，需要设数组num和数组position来分别存放总个数和正确位置。

如图所示：

稀疏矩阵a(n行m列,非零元素数为t)采用三元组b表示,那么在三元组中访问a[i][j]所需,数据结构——用C语言描述,矩阵,算法,数据结构,c语言

数组num的计算方法：

将三元组表from扫描一遍，对于其中列号为col的非零元素，给相应的num数组中下标为col的元素加1。

数组position的计算方法：

1、position[1] = 1：三元组表from的第1列的第一个非零元素在三元组表to中的下标值为1。

2、position[col] = position[col - 1] + num[col - 1]。文章来源地址https://www.toymoban.com/news/detail-740479.html

2.2.2 算法实现

void FastTransposeTSMatrix(TSMatrix *from, TSMatrix *to) {
    to->len = from->len;
    to->n = from->m;
    to->m = from->n;
    if (to->len) {
        int i, j, col;
        int num[MAXSIZE], position[MAXSIZE];
        
        /* 计算num数组 */
        for (i = 1; i <= from->n; ++i)
            num[i] = 0;
        for (i = 1; i <= from->len; ++i)
            ++num[from->data[i].col]; 

        /* 计算position数组 */
        position[1] = 1;
        for (col = 2; col <= from->n; ++col) 
            position[col] = position[col - 1] + num[col - 1];

        /* 将被转置矩阵的三元组表from从头至尾扫描一次，实现矩阵转置 */
        for (i = 1; i <= from->len; ++i) { 
            col = from->data[i].col; j = position[col];

            to->data[j].row = from->data[i].col;
            to->data[j].col = from->data[i].row;
            to->data[j].e = from->data[i].e;
            /* position[col]加1，指向下一个列号为col的非零元素在三元组表to中的下标值*/
            ++position[col]; 
        }
    }
}

到了这里，关于稀疏矩阵（表示、转置）的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！