Python 第三代非支配排序遗传算法(NSGA-III)求解多目标高次函数的帕累托前沿-Toy模板网

这篇具有很好参考价值的文章主要介绍了Python 第三代非支配排序遗传算法(NSGA-III)求解多目标高次函数的帕累托前沿。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

系列文章目录

文章目录

前言

我前面有博客介绍了第二代非支配排序遗传算法(NSGA-II)求解多目标高次函数的帕累托前沿的代码，本篇博客则是介绍NSGA-III求解多目标高次函数的帕累托前沿。

一、模型的建立

研究的模型为：min(y1=,x[-10,10]), min(y2=,x[-10,10])。即求解两个目标函数最小值的问题。

二、算法的步骤

步骤如下：

初始化种群：首先，根据给定的自变量范围和种群大小，随机生成一组初始解，并用自变量的取值来表示每个个体。
目标函数评估：接下来，对于种群中的每一个个体，计算出其对应的目标函数值。
非支配排序：将种群中的个体按照非支配排序的方法进行排序，以便于进行进一步的选择和交叉。
拥挤度距离计算：针对当前排好序的所有非支配解，计算其在目标函数空间中的拥挤度距离，以便于在后续的交叉和变异过程中能够更加有效地保持多样性。
分配密度估计：针对当前的非支配解和权重向量，计算出每个个体所占据的密度估计，以便于在进行交叉时，选择距离相近的两个个体进行配对。
选择和交叉：采用确定性方法或者随机方法选择一组个体进行交叉，得到新的一代种群。
变异：对每个个体进行变异操作，以增加种群的多样性。
更新种群：将新生成的种群与原始种群进行合并，并且保留当前轮次中的非支配解（即精英保留策略）。
迭代：循环执行上述所有步骤，直到满足停止条件。
输出结果：最后，从最后一代种群中提取出所有的帕累托最优解，并输出结果。

首先设置了一些参数，包括种群大小、进化代数、交叉概率、变异概率、目标函数个数和自变量取值范围等。接着定义了一个Individual类，用来表示每一个个体的自变量和目标函数值。在初始化种群过程中，采用随机方式生成个体，并进行进化操作。

在每一次迭代中，首先按照非支配排序算法对所有个体进行排名，并计算出相应的拥挤度距离。然后根据权重向量和参考点计算出个体的密度估计，并进行交叉和变异操作。最后，通过对最后一代种群中的所有解进行筛选，提取出帕累托最优解，并输出结果。

三、代码的实现

代码如下：

import random
import matplotlib.pyplot as plt
import numpy as np
import time

start_time=time.time()

# 设置参数
pop_size = 100  # 种群大小
gen_size = 100  # 进化代数
pc = 1  # 交叉概率
pm = 0.3  # 变异概率
num_obj = 2  # 目标函数个数
x_range = (-10, 10)  # 自变量取值范围


# 定义自变量的类
class Individual:
    def __init__(self, x):
        self.x = x
        self.objs = [None] * num_obj
        self.rank = None
        self.distance = 0.0

    # 计算目标函数的值
    def evaluate(self):
        self.objs[0] = self.x * self.x
        self.objs[1] = (2 - self.x) ** 2


# 初始化种群
pop = [Individual(random.uniform(*x_range)) for _ in range(pop_size)]

# 进化
for _ in range(gen_size):
    print(f"第{_}次迭代")
    # 计算目标函数的值
    for ind in pop:
        ind.evaluate()

    # 非支配排序
    fronts = [set()]
    for ind in pop:
        ind.domination_count = 0
        ind.dominated_set = set()

        for other in pop:
            if ind.objs[0] < other.objs[0] and ind.objs[1] < other.objs[1]:
                ind.dominated_set.add(other)
            elif ind.objs[0] > other.objs[0] and ind.objs[1] > other.objs[1]:
                ind.domination_count += 1

        if ind.domination_count == 0:
            ind.rank = 1
            fronts[0].add(ind)

    rank = 1
    while fronts[-1]:
        next_front = set()

        for ind in fronts[-1]:
            ind.rank = rank

            for dominated_ind in ind.dominated_set:
                dominated_ind.domination_count -= 1

                if dominated_ind.domination_count == 0:
                    next_front.add(dominated_ind)

        fronts.append(next_front)
        rank += 1

    # 计算拥挤度距离
    pop_for_cross = set()
    for front in fronts:
        if len(front) == 0:
            continue

        sorted_front = sorted(list(front), key=lambda ind: ind.rank)
        for i in range(num_obj):
            sorted_front[0].objs[i] = float('inf')
            sorted_front[-1].objs[i] = float('inf')
            for j in range(1, len(sorted_front) - 1):
                delta = sorted_front[j + 1].objs[i] - sorted_front[j - 1].objs[i]
                if delta == 0:
                    continue

                sorted_front[j].distance += delta / (x_range[1] - x_range[0])

        front_list = list(sorted_front)
        front_list.sort(key=lambda ind: (-ind.rank, -ind.distance))
        selected_inds = front_list
        if len(pop_for_cross) + len(selected_inds) <= pop_size:
            pop_for_cross.update(selected_inds)
        elif len(pop_for_cross) + len(selected_inds) >= pop_size and len(pop_for_cross) < pop_size:
            part_selected_inds = selected_inds[:(pop_size - len(pop_for_cross))]
            pop_for_cross.update(part_selected_inds)
            break

    # 计算每个目标函数的权重向量和参考点
    """
当num_obj=2时，定义的ref_vectors列表内容为[[1.0, 0], [0, 1.0]]，其中包含了所有的权重向量。因为在该问题中我们有两个目标函数，所以共需要两个权重向量。

那么ref_vectors中的第一个子列表[1.0, 0]代表的是第一个目标函数的权重向量，其中1.0表示在第一个目标函数上最大化目标函数值，0表示在第二个目标函数上最小化目标函数值。

同理，ref_vectors中的第二个子列表[0, 1.0]代表的是第二个目标函数的权重向量，其中1.0表示在第二个目标函数上最大化目标函数值，0表示在第一个目标函数上最小化目标函数值。

总之，ref_vectors中的每个子列表代表一个不同的权重向量，它们分别控制着各个目标函数的优化方向。
    """
    ref_vectors = []
    for i in range(num_obj):
        vec = [0] * num_obj
        vec[i] = 1.0
        ref_vectors.append(vec)

    for vec in ref_vectors:
        # 根据权重向量vec，计算出一个参考点ref_point，在目标函数空间中代表着该权重下的理想解。
        ref_point = [vec[j] * x_range[j] for j in range(num_obj)]
        # 根据权重向量vec，计算出一个参考点ref_point，在目标函数空间中代表着该权重下的理想解。
        weighted_objs = [(ind.objs[k] - ref_point[k]) * vec[k] for ind in pop_for_cross for k in range(num_obj)]
        # 对于当前的所有个体，在目标函数空间中的加权距离进行排序。
        sorted_objs = sorted(weighted_objs)
        # 在排序后的加权距离列表中选择中位数值，并将其作为拥挤度距离的计算基准。
        median_objs = [sorted_objs[len(sorted_objs) // 2 + offset] for offset in (-1, 0, 1)]
        # 根据当前参考点和中位数计算出其到其他个体最短距离。
        min_dist = np.linalg.norm(np.array(median_objs[:num_obj]) - ref_point)
        # 遍历种群中的每个个体ind，计算其在目标函数空间中针对当前权重向量vec的加权距离，并与之前计算出的最短距离min_dist比较，得到本次遍历中所有个体所能达到的最小距离值。
        for ind in pop_for_cross:
            dist = np.linalg.norm(np.array([(ind.objs[k] - ref_point[k]) * vec[k] for k in range(num_obj)]))
            if dist < min_dist:
                min_dist = dist
        # 再次遍历种群中的每个个体ind，根据之前得到的最小距离值，计算该个体的拥挤度距离。这里采用了一种计算公式，即将每个个体的拥挤度距离设定为其当前拥挤度距离值加上其到其他个体最小距离的倒数。
        for ind in pop_for_cross:
            dist = np.linalg.norm(np.array([(ind.objs[k] - ref_point[k]) * vec[k] for k in range(num_obj)]))
            ind.distance += (min_dist / (dist + min_dist))

    # 通过拥挤度距离与分配密度估计来选择进行交叉的个体
    new_pop = set()
    while len(new_pop) < pop_size:
        pool = random.sample(pop_for_cross, 2)
        pool_dist = [ind.distance for ind in pool]
        parent1 = pool[np.argmax(pool_dist)]
        parent2 = pool[1 - np.argmax(pool_dist)]

        child_x = (parent1.x + parent2.x) / 2
        delta_x = abs(parent1.x - parent2.x)
        child_x += delta_x * random.uniform(-1, 1)

        child = Individual(child_x)
        new_pop.add(child)

    # 变异
    for ind in new_pop:
        if random.random() < pm:
            delta_x = random.uniform(-1, 1) * (x_range[1] - x_range[0])
            ind.x += delta_x
            ind.x = max(x_range[0], min(x_range[1], ind.x))

    # 更新种群,把原来的精英（pop_for_cross）保留下来。即精英保留策略
    pop = list(new_pop) + list(pop_for_cross)

# 输出最优解集合
for ind in pop:
    ind.evaluate()

pareto_front = set()
for ind in pop:
    dominated = False
    for other in pop:
        if other.objs[0] < ind.objs[0] and other.objs[1] < ind.objs[1]:
            dominated = True
            break
    if not dominated:
        pareto_front.add(ind)

print("Pareto front:")
for ind in pareto_front:
    print(f"x={ind.x:.4f}, y1={ind.objs[0]:.4f}, y2={ind.objs[1]:.4f}")

# 可视化
plt.scatter([ind.objs[0] for ind in pop], [ind.objs[1] for ind in pop], c='gray', alpha=0.5)
plt.scatter([ind.objs[0] for ind in pareto_front], [ind.objs[1] for ind in pareto_front], c='r')
plt.xlabel('Objective 1')
plt.ylabel('Objective 2')
end_time=time.time()
print(f"求得的帕累托解的个数为：{len(pareto_front)}")
print(f"\n程序执行时间为：{end_time-start_time}")
print("加入我的qq群，大家一起讨论管理、规划类问题的算法\n群里我会不定期上传一些我自己和其他大神的算法源码\n群号为：808756207")
plt.show()

四、输出的结果

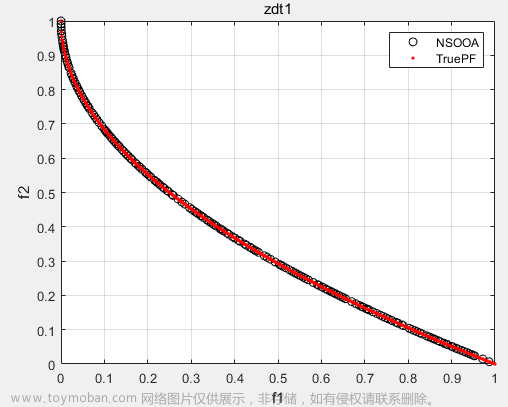
分别输出了各个帕累托前沿解及帕累托前沿的离散图像，红色点部分为帕累托前沿解：

第三代遗传算法,项目管理算法,工商管理算法,Python 数据分析,python,数据挖掘,机器学习,numpy,数学建模,算法

总结

因为NSGA-III增加了几个参数，因此效率很依赖于对这些参数的调整，总体运行速度是低于NSGA-II的，但是它和NSGA-II想比，还是具备以下优点：

高效性：NSGA-III和NSGA-II都采用非支配排序和拥挤度距离计算策略，能够有效地维护种群的多样性，从而提高收敛速度和搜索效率。
稳健性：NSGA-III不依赖于特定的问题结构或形式。这些特性使得该算法具有良好的稳健性和可移植性，适用于各种多目标优化问题。
解的质量：NSGA-III在针对分布不均匀的Pareto前沿的搜索能力上比NSGA-II更出色，解的质量更高。
多样性：NSGA-III比NSGA-II更加注重多样性的保持，因此能够在搜索过程中保持更好的种群多样性，并找到更多的Pareto最优解。
可扩展性：NSGA-III和NSGA-II都可以很容易地扩展到处理带约束的多目标优化问题，例如在NSGA-III基础上进行改进，提出了NSGA-III-G和MOEA/D-NSGA-III等算法。

总的来说，NSGA-III和NSGA-II是经典的多目标优化算法，在实际应用中广泛使用。两种算法都有各自的优势和适用范围，在具体问题中需要根据实际情况选择合适的算法。文章来源地址https://www.toymoban.com/news/detail-740485.html

到了这里，关于Python 第三代非支配排序遗传算法(NSGA-III)求解多目标高次函数的帕累托前沿的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！