图论08-图的建模-状态的表达与理解 - 倒水问题为例-Toy模板网

这篇具有很好参考价值的文章主要介绍了图论08-图的建模-状态的表达与理解 - 倒水问题为例。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

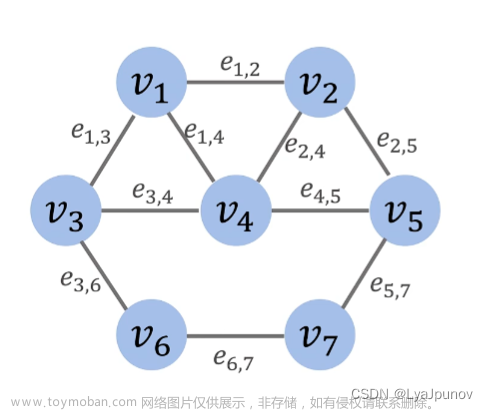
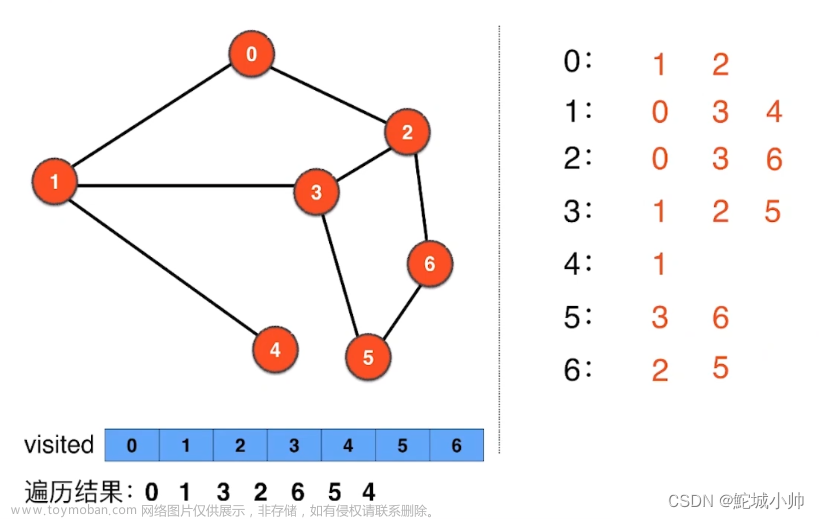
状态的表达

例题1

图论08-图的建模-状态的表达与理解 - 倒水问题为例,图论,图论

从初始的(x，y)状态，到最后变成（4，？）或者（？，4）.

本道题对于(x，y)的状态，可以使用10x+y进行表达，也就是变成了一个数字，分别放在不同的数位上。
但是本状态的表示方法不适用单个数组超过9的，因为一个数位只能表示0-9.。

涉及思想：状态压缩

题解

1 终止条件：有一个数位为4

if(next / 10 == 4 || next % 10 == 4) {
    end = next;
    return;
}

2 状态的改变：a表示十位数，b表示个位数

重复添加满水不影响结果

a = cur / 10, b = cur % 10;

要达到（4，？）或者（？，4）的办法文章来源地址https://www.toymoban.com/news/detail-740789.html

a桶灌满5升水
b桶灌满3升水
a桶的水倒掉
b桶的水倒掉
a桶中的水倒进b桶中 --> 最多能倒a升，还能倒b桶剩余空闲容量=(3-b桶当前容量)
b桶中的水倒进a桶中

nexts.add(5 * 10 + b);
nexts.add(a * 10 + 3);
nexts.add(a * 10 + 0);
nexts.add(0 * 10 + b);

int x = Math.min(a, 3 - b);
nexts.add((a - x) * 10 + (b + x));

int y = Math.min(b, 5 - a);
nexts.add((a + y) * 10 + (b - y));

3 其他设置

访问数组用于记录访问过的状态

 boolean[] visited = new boolean[100];

队列用于记录访问的每个节点的状态

Queue<Integer> queue = new LinkedList<>();

记录上一个状态

pre = new int[100];

记录状态变化
- 首先要把pre数组填好，根据pre数组将遍历的过程从最终结果向前找初始状态。最终再翻转链表。
- 做标记设置end = -1
  如果end倒最后还是-1，说明问题没有解。

import java.util.*;
import java.util.ArrayList;

public class WaterPuzzle {

    private int[] pre;
    private int end = -1;

    public WaterPuzzle(){

        Queue<Integer> queue = new LinkedList<>();
        boolean[] visited = new boolean[100];
        pre = new int[100];

        queue.add(0);
        visited[0] = true;
        while (!queue.isEmpty()){
            int cur = queue.remove();
            int a = cur / 10, b = cur % 10;
            // max a = 5, max b = 3

            ArrayList<Integer> nexts = new ArrayList<>();
            nexts.add(5 * 10 + b);
            nexts.add(a * 10 + 3);
            nexts.add(a * 10 + 0);
            nexts.add(0 * 10 + b);

            int x = Math.min(a, 3 - b);
            nexts.add((a - x) * 10 + (b + x));

            int y = Math.min(b, 5 - a);
            nexts.add((a + y) * 10 + (b - y));

            for(int next: nexts)
                if(!visited[next]){
                    queue.add(next);
                    visited[next] = true;
                    pre[next] = cur;

                    if(next / 10 == 4 || next % 10 == 4) {
                        end = next;
                        return;
                    }
                }
        }
    }

    public Iterable<Integer> result(){

        ArrayList<Integer> res = new ArrayList<>();
        if(end == -1) return res;

        int cur = end;
        while(cur != 0){
            res.add(cur);
            cur = pre[cur];
        }
        res.add(0);
        Collections.reverse(res);
        return res;
    }

    public static void main(String[] args){
        System.out.println((new WaterPuzzle()).result());
    }
}

例题2 力扣773 滑动谜题

Java

/// Leetcode 773

import java.util.ArrayList;
import java.util.Queue;
import java.util.LinkedList;
import java.util.HashMap;


public class Solution {

    private int[][] dirs = {{-1, 0}, {0, 1}, {1, 0}, {0, -1}};

    public int slidingPuzzle(int[][] board) {

        Queue<String> queue = new LinkedList<>();
        HashMap<String, Integer> visited = new HashMap<>();

        String initalState = boardToString(board);
        if(initalState.equals("123450")) return 0;

        queue.add(initalState);
        visited.put(initalState, 0);
        while(!queue.isEmpty()){
            String cur = queue.remove();

            ArrayList<String> nexts = getNexts(cur);

            for(String next: nexts)
                if(!visited.containsKey(next)){
                    queue.add(next);
                    visited.put(next, visited.get(cur) + 1);
                    if(next.equals("123450"))
                        return visited.get(next);
                }
        }
        return -1;
    }

    private ArrayList<String> getNexts(String s){

        int[][] cur = stringToBoard(s);

        int zero;
        for(zero = 0; zero < 6; zero ++)
            if(cur[zero / 3][zero % 3] == 0)
                break;

        ArrayList<String> res = new ArrayList<>();
        int zx = zero / 3, zy = zero % 3;
        for(int d = 0; d < 4; d ++){
            int nextx = zx + dirs[d][0], nexty = zy + dirs[d][1];
            if(inArea(nextx, nexty)){
                swap(cur, zx, zy, nextx, nexty);
                res.add(boardToString(cur));
                swap(cur, zx, zy, nextx, nexty);
            }
        }
        return res;
    }

    private boolean inArea(int x, int y){
        return x >= 0 && x < 2 && y >= 0 && y < 3;
    }

    private void swap(int[][] board, int x1, int y1, int x2, int y2){
        int t = board[x1][y1];
        board[x1][y1] = board[x2][y2];
        board[x2][y2] = t;
    }

    private String boardToString(int[][] board){
        StringBuilder sb = new StringBuilder();
        for(int i = 0; i < 2; i ++)
            for(int j = 0; j < 3; j ++)
                sb.append(board[i][j]);
        return sb.toString();
    }

    private int[][] stringToBoard(String s){
        int[][] board = new int[2][3];
        for(int i = 0; i < 6; i ++)
            board[i / 3][i % 3] = s.charAt(i) - '0';
        return board;
    }

    public static void main(String[] args){

        int[][] board = {{1, 2, 3}, {4, 0, 5}};
        System.out.println((new Solution()).slidingPuzzle(board));
    }
}

C++

class Solution {
public:
    int slidingPuzzle(vector<vector<int>>& board) {
//记录最终状态
    const string sol = "123450";

    const int m = 2, n = 3;
    const int dirs[4][2] = {{-1, 0}, {0, 1}, {1, 0}, {0, -1}};

//记录初始状态，使用字符串记录
    string init;
    for (auto &line: board) {
        for (auto &grid: line) {
            init.push_back('0' + grid);
        }
    }

//构造队列，并初始化
    queue<string> q{{init}};

//设置unordered_set，记录访问状态
    unordered_set<string> vis{{init}};

//记录步数
    int ans = 0;

//开始BFS
    while (!q.empty()) {
        int size = q.size();
        for (int i = 0; i < size; ++i) {
            auto &p = q.front();
            //出口
            if (p == sol) {
                return ans;
            }

            //先找0号的位置
            int idx0 = p.find('0');

            //四联通拓展
            for (int a = 0; a < 4; ++a) {
                //求0号元素的二维新坐标
                int nx = idx0 / n + dirs[a][0], ny = idx0 % n + dirs[a][1];
                //求0号元素映射到一维数组中的坐标
                int idx1 = nx * n + ny;
                //判断边界
                if (nx >= 0 && nx < m && ny >= 0 && ny < n) {
                    //交换两个元素的位置
                    swap(p[idx0], p[idx1]);
                    //如果当前状态没有测试过
                    if (!vis.count(p)) {
                        //加入访问数组
                        vis.insert(p);
                        //入队
                        q.push(p);
                    }
                    //恢复原来的状态，继续交换位置然后将状态入队列
                    swap(p[idx0], p[idx1]);
                }
            }
        q.pop();
        }
    //对头出队的时候，开始移动到下一个状态，因此步数+1
    ++ans;
    }
    return -1;
    }
};