1. 遍历的意义
1.1 图的遍历
图的遍历是指按照一定规则访问图中的所有顶点,以便获取图的信息或执行特定操作。常见的图遍历算法包括深度优先搜索(DFS)和广度优先搜索(BFS)。
深度优先搜索(DFS):从起始顶点开始,递归或使用栈的方式访问相邻的顶点,直到所有顶点都被访问过为止。DFS通过探索图的深度来遍历图,一直沿着路径向下直到无法继续,然后回溯到前一个顶点,继续探索其他路径。
广度优先搜索(BFS):从起始顶点开始,逐层访问其相邻顶点,先访问距离起始顶点最近的顶点,然后依次访问距离起始顶点更远的顶点。BFS通过探索图的广度来遍历图,先访问离起始顶点最近的顶点,然后依次访问其他相邻的顶点。
这两种遍历算法可以用于有向图和无向图,并且可以用来解决很多与图相关的问题,例如寻找路径、判断连通性、查找最短路径等。
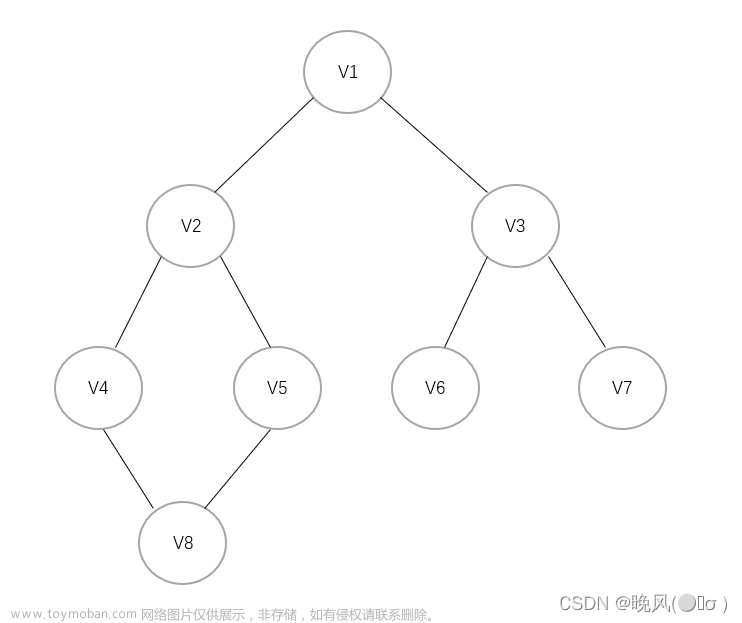
1.2 树的遍历
树的遍历算法题链接:树结构及遍历
示例-前序遍历:
class TreeNode {
int val;
TreeNode left;
TreeNode right;
public TreeNode(int val) {
this.val = val;
}
}
public class TreeTraversal {
public void preorderTraversal(TreeNode root) {
if (root == null) {
return;
}
System.out.print(root.val + " "); // 访问根节点
preorderTraversal(root.left); // 前序遍历左子树
preorderTraversal(root.right); // 前序遍历右子树
}
}
2. 图的深度优先遍历-前序遍历
public class GraphDFS {
private Graph G; // 顶点数
private boolean [] visited; // 边数
private ArrayList<Integer> order = new ArrayList();
public GraphDFS(Graph G){
this.G = G;
visited = new boolean[G.V()];
dfs(0);
}
private void dfs(int v){
visited[v] = true;
order.add(v);
for (int w : G.adj(v)) {
if (!visited[w]) {
dfs(w);
}
}
}
public Iterable<Integer> order(){
return order;
}
}该递归方法按照以下步骤进行遍历:
- 选择一个起始节点
v进行遍历,并将其标记为已访问。 - 输出当前节点的值。
- 对于当前节点
v的每个邻接节点w,如果邻接节点w尚未访问,则递归调用该方法,以节点w作为新的起始节点,继续遍历。 - 重复步骤2和步骤3,直到所有节点都被访问过。

该递归方法的关键在于递归调用。通过递归,当遍历到一个节点的邻接节点时,会先访问邻接节点,然后再递归访问邻接节点的邻接节点,以此类推,直到遍历完所有可达的节点。这样就实现了深度优先搜索的效果。
在遍历过程中,使用一个布尔类型的数组 visited 来标记节点是否已访问。初始时,所有节点的访问状态都设置为 false。在遍历过程中,将访问过的节点标记为 true,以避免重复访问。
通过递归调用和节点的访问状态标记,该方法能够深入到图的每个连通分量,并逐个访问每个节点,确保不会漏掉任何节点。
代码运行结果:
public static void main(String[] args) {
Graph graph = new Graph("g.txt");
GraphDFS graphDFS = new GraphDFS(graph);
System.out.println(graphDFS.order());
}
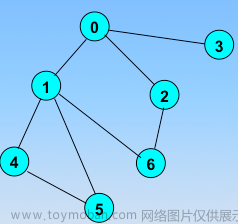
[0, 1, 2, 3, 4, 5, 6]
Process finished with exit code 0上述优先遍历逻辑的问题
该方法在遍历过程中只能遍历到与起始节点连通的顶点,对于不连通的顶点是无法遍历到的。
在构造函数 GraphDFS(Graph G) 中,使用深度优先搜索算法进行遍历的起始节点是固定的,即始终从顶点0开始。然后在 dfs(int v) 方法中,通过递归调用遍历与当前节点相邻的节点。由于该算法的起始节点是固定的,因此只能访问到与起始节点连通的顶点。
如果图中存在多个连通分量(即图中有多个独立的子图),且起始节点只属于其中一个连通分量,那么其他连通分量中的顶点是无法通过该方法遍历到的。
要遍历整个图,需要对每个顶点都调用深度优先搜索算法进行遍历,以确保遍历到所有的顶点。可以通过循环遍历图中的每个顶点,并对未访问过的顶点调用深度优先搜索方法来实现。
改进构造器方法:
public GraphDFS(Graph G){
this.G = G;
visited = new boolean[G.V()];
for (int v = 0; v < G.V(); v++ ){
if (!visited[v]){
dfs(v);
}
}
}3. 图的深度优先遍历-后序遍历
public class GraphDFS {
private Graph G; // 顶点数
private boolean [] visited; // 边数
private ArrayList<Integer> pre = new ArrayList(); // 先序遍历
private ArrayList<Integer> post = new ArrayList(); // 后序遍历
public GraphDFS(Graph G){
this.G = G;
visited = new boolean[G.V()];
for (int v = 0; v < G.V(); v++ ){
if (!visited[v]){
dfs(v);
}
}
}
private void dfs(int v){
visited[v] = true;
pre.add(v);
for (int w : G.adj(v)) {
if (!visited[w]) {
dfs(w);
}
}
post.add(v);
}
public Iterable<Integer> pre(){
return pre;
}
public Iterable<Integer> post(){
return post;
}
public static void main(String[] args) {
Graph graph = new Graph("g.txt");
GraphDFS graphDFS = new GraphDFS(graph);
System.out.println(graphDFS.pre());
System.out.println(graphDFS.post());
}
}上述代码实现了图的后序遍历。主要的实现思路如下:
在GraphDFS类中,定义了一个私有成员变量pre和post,它们分别用于存储前序遍历和后序遍历的顶点顺序。
在GraphDFS的构造函数中,遍历图中的所有顶点。对于每个未被访问过的顶点,调用dfs方法进行深度优先搜索。
在dfs方法中,首先将当前顶点标记为已访问,并将其添加到pre列表中,表示前序遍历的顺序。
然后遍历当前顶点的邻接顶点,如果邻接顶点未被访问过,则递归调用dfs方法进行深度优先搜索。在递归回溯时,将当前顶点添加到post列表中,表示后序遍历的顺序。
最后,通过调用pre()和post()方法,可以获取到前序遍历和后序遍历的顶点顺序。
4. 复杂度分析
优先搜索的过程中,每个顶点只会被访问一次。
对于稀疏图(边数接近顶点数的数量级)而言,深度优先遍历的时间复杂度可以近似地表示为O(V+E),其中V是顶点数,E是边数。这是因为在每个顶点上进行一次访问的操作,以及遍历每条边的操作都需要一定的时间。
对于稠密图(边数接近V^2的数量级)而言,深度优先遍历的时间复杂度可以近似地表示为O(V^2),其中V是顶点数。这是因为在每个顶点上进行一次访问的操作,以及遍历每个顶点的邻接列表的操作都需要一定的时间。
上述示例中,是稀疏图,所以,其时间复杂度为 O(V+E)。
 文章来源:https://www.toymoban.com/news/detail-740952.html
文章来源:https://www.toymoban.com/news/detail-740952.html
总结而言,深度优先遍历的时间复杂度与图的规模有关,一般情况下可以近似表示为O(V+E)或O(V^2)。文章来源地址https://www.toymoban.com/news/detail-740952.html
到了这里,关于图论与算法(3)图的深度优先遍历的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!