前言
因为毕业设计论文研究的课题跟LQR控制算法相关，博主这几天恶补了一下之前学过的东西，像自动控制，现代控制，建模等等，于是在这里用一个简单的一阶倒立摆模型来记录一下，将复习的内容简单应用一下。
一、系统建模
对于一个简单的小车+一个摆杆组合成的一阶倒立摆模型（假设地面光滑）如图:
对于小车来说：水平方向受到F(x)和
H
x
H_{x}
Hx两个力，垂直方向上小车在这里不研究
对于摆杆来说：水平方向上受到
H
x
H_{x}
Hx一个力，垂直方向上受到
H
y
H_{y}
Hy和重力mg
参数说明：x是水平上的位移，L（图中小写）是长度，g是重力加速度，m是摆杆的质量，M是车子重量，下面进行系统的运动学建模。
二、运动方程
对小车：
对摆杆水平方向上：
其中：
整理可以得到系统的第一个方程：
对摆杆垂直方向上：
其中：
除去水平和垂直方向，摆杆还有一个绕着质心的旋转：
其中绕质心旋转的刚体的 转动惯量：
由以上得到系统第二个运动方程：
写成矩阵形式：
三、LQR算法
1.LQR算法
这里相关介绍就不说了，可以看看DR_CAN现代控制课程
2.线性化处理
我们知道当系统处于稳定或者接近稳定时，θ->0，由极限的知识可以得到：
那么在平衡点附近，系统的运动方程就可以简化成：
定义系统的状态变量为 ( X 1 X 2 X 3 X 4 ) = ( x x ′ θ θ ′ ) \bigl(\begin{smallmatrix} X_{1} &X_{2} & X_{3} & X_{4} \end{smallmatrix}\bigr)=\begin{pmatrix} x & {x}' & \theta & {\theta }' \end{pmatrix} (X1X2X3X4)=(xx′θθ′)，施加给小车的力为 F x F_{x} Fx，系统的输出为位移 x x x,可以得到系统的状态方程为：
输出：
在这里假设 g = 9.8 m / s 2 , M = 4 , m = 0.5 , L = 1 g = 9.8m/s^{2},M = 4,m = 0.5, L = 1 g=9.8m/s2,M=4,m=0.5,L=1,那么状态矩阵:
控制矩阵：
3.能控性质分析
利用李雅普诺夫定理（可以参考DR_CAN现代控制课程）：
> A=[0 1 0 0;0 0 -0.8909 0;0 0 0 1;0 0 8.0182 0]
> B=[0;0.2424;0;-0.1818]
> Co=ctrb(A，B)
> rank(Co)
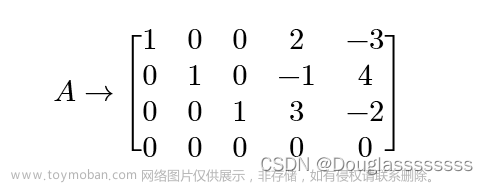
最后算出来是
r
a
n
k
=
4
rank =4
rank=4满秩，故系统是可控的。
又因为A的特征值通过matlab算出来有正根，故此时的系统是发散的。因此要设置反馈矩阵K。
[v,d]=eig(A)
v =
1.0000 -1.0000 -0.0368 0.0368
0 0.0000 -0.1041 -0.1041
0 0 0.3310 -0.3310
0 0 0.9372 0.9372
d =
0 0 0 0
0 0 0 0
0 0 2.8316 0
0 0 0 -2.8316
4 .LQR控制器设计
增加反馈回路：
就是要求解一个矩阵 K K K,使得：
有最小值。其中 Q Q Q越大，说明状态 x x x收敛得快， R R R越大，说明需要的输入很小，也就是涉及到系统能量的问题。所以如何选择 Q Q Q和 R R R对于系统来说很重要。
这里我先选择 Q = E , R = E Q=E,R=E Q=E,R=E:利用MATLAB求解：
Q = eye(4);
R = eye(1);
K_lqr = lqr(A,B,Q,R);
求得 K = ( − 1 − 3.8734 − 112.7199 − 40.2095 ) K=\begin{pmatrix} -1 & -3.8734 & -112.7199 &-40.2095 \end{pmatrix} K=(−1−3.8734−112.7199−40.2095)
如果我想X或者一些状态变量收敛的更快一点，不考虑输入的情况下:
R = E R=E R=E依然，此时求得 K 1 = ( − 10.0000 − 17.2252 − 184.5921 − 66.6912 ) K_{1}=\begin{pmatrix} -10.0000 & -17.2252 & -184.5921 & -66.6912 \end{pmatrix} K1=(−10.0000−17.2252−184.5921−66.6912)
**如果我想输入不需要那么大，不关系系统状态的收敛情况：**令 R = 100 , Q = E R=100,Q=E R=100,Q=E，求得:
下面通过Simulink仿真可得 ：
符合预期结果。
5.Simulink建模
文章来源：https://www.toymoban.com/news/detail-741056.html
总结
通过这个例子唤醒之前学过的知识，毕设的内容跟双轮平衡车相关，到时候再更新吧。文章来源地址https://www.toymoban.com/news/detail-741056.html
到了这里，关于一阶倒立摆简单模型的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
