这篇具有很好参考价值的文章主要介绍了线性代数1：线性方程和系统。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。
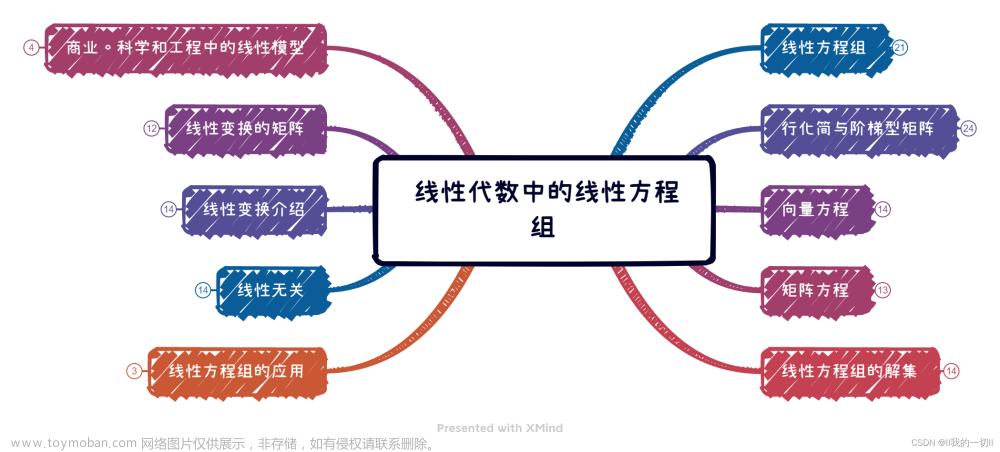
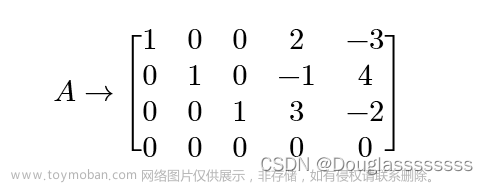
图片来自施泰德博物馆
通过这些文章，我希望巩固我对这些基本概念的理解，同时如果可能的话，通过我希望成为一种基于直觉的数学学习方法为其他人提供额外的清晰度。如果有任何错误或机会需要我进一步阐述，请分享，我可以进行必要的修改。
这是关于线性代数基础知识的持续系列文章的第一个补充，线性代数是机器学习背后的基础数学。本文最好与David C. Lay，Steven R. Lay和Judi J. McDonald的线性代数及其应用一起阅读。将此系列视为外部配套资源。文章来源：https://www.toymoban.com/news/detail-741396.html
线性方程组和线性方程组在金融、工程、化学、计算机科学、统计学和物理学等领域具有各种实际应用。在化学中，线性方程用于文章来源地址https://www.toymoban.com/news/detail-741396.html
到了这里，关于线性代数1：线性方程和系统的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处： 如若内容造成侵权/违法违规/事实不符，请点击违法举报进行投诉反馈，一经查实，立即删除！
1.解线性方程组 2.线性方程组解的情况 3.线性方程组的两个基本问题 1.阶梯型矩阵性质 2.简化阶梯型矩阵（具有唯一性） 3.行化简算法 4.线性方程组的解 1.R^2中的向量 2.R^2中的几何表示 3.R^n中的向量 4.线性组合与向量方程 5.span{v},span{u,v}的几何解释 1.定义 2.定理 3.解的存在性
本文参考www.deeplearningbook.org一书第二章2.3 Identity and Inverse Matrices 2.4 Linear Dependence and Span 本文围绕 线性方程求解 依次介绍矩阵的逆、线性组合、线性独立等线性代数的基础知识点。 本文主要围绕求解线性方程展开，我们先把线性方程写出来，方程如下： 其中，是已知的；，
定理1 设A为mXn矩阵,则 (1)齐次线性方程组AX=0 只有零解的充分必要条件是r(A)=n; (2)齐次线性方程组AX=0 有非零解(或有无数个解)的充分必要条件是r(A)＜n 推论1 设A为n阶矩阵,则 (1)齐次线性方程组AX=0只有零解的充分必要条件是|A|≠0; (2)齐次线性方程组AX=0有非零解(或有无数个解)的
4.1 线性方程组 ● 由二元一次方程的消元法，交换两个方程，用非零数乘以某个方程，某方程乘以k倍加到另一方程。这个与矩阵的初等行变换相似。 ● 将上面方程组的未知数去掉，将系数写在一个矩阵中。就可以表示该方程组。并可以通过矩阵的初等行变换求解。 4.2 线性
一、矩阵形式 经过初等行变换化为阶梯形矩阵。当，有解；当，有非零解。 有解，等价于 可由线性表示 克拉默法则：非齐次线性方程组中，系数行列式，则方程组有唯一解，且唯一解为 其中是中第i列元素（即的系数）替换成方程组右端的常数项所构成的行列式。 二、向量
如何利用行列式，矩阵求解线性方程组。 用矩阵方程表示 齐次线性方程组：Ax=0； 非齐次线性方程组：Ax=b. 可以理解 齐次线性方程组 是特殊的 非齐次线性方程组 如何判断线性方程组的解 其中R(A)表示矩阵A的秩 B表示A的增广矩阵 n表示末知数个数 增广矩阵 矩阵的秩 秩r= 未知
齐次线性方程组是指所有方程的常数项均为零的线性方程组，即形如 A x = 0 Ax=0 A x = 0 的方程组。 其中，矩阵 A A A 是一个 m × n m times n m × n 的矩阵，向量 x x x 是一个 n n n 维列向量， 0 mathbf{0} 0 是一个 m m m 维零向量。 齐次线性方程组有以下性质： 1. 性质1 齐次线性方程组的
欢迎回到系列文章的第三篇文章，内容是线性代数的基础知识，线性代数是机器学习背后的基础数学。在我之前的文章中，我介绍了梯队矩阵形式。本文将介绍向量、跨度和线性组合，并将这些新想法与我们已经学到的内容联系起来。本文最好与David C. Lay，Steve
如果你进行的矩阵乘法涉及一个线性方程组 Ax = b，并且你乘以一个可逆矩阵 M，且产生新的方程组 M(Ax) = Mb，那么这两个系统是等价的；它们具有相同的解集。这是因为可逆矩阵的乘法可以视为一个可逆的线性变换，不会改变方程解的存在性或唯一性。 换句话说，如果你将原
承接前文，继续学习线性方程组的内容，从方程组的通解开始。 （1）基础解系 —— 设 r ( A ) = r n r(A)=rn r ( A ) = r n ，则 A X = 0 pmb{AX=0} A X = 0 所有解构成的解向量组的极大线性无关组称为方程组 A X = 0 pmb{AX=0} A X = 0 的一个基础解系。基础解系中所含有的线性无关的解向量的个
