模拟集成电路笔记 | 第一部分 | Chapter 1-3-Toy模板网

这篇具有很好参考价值的文章主要介绍了模拟集成电路笔记 | 第一部分 | Chapter 1-3。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

模拟集成电路笔记 | 第一部分 | Chapter 1-3

本系列笔记是参考书籍《CMOS模拟集成电路》和中科大相关课程课件而做成，笔记第一版为手写版，现在在手写版的基础上重新编写第二版（markdown格式）。

如想获得更好的阅读体验，可进入 01-CMOS模拟集成电路笔记

第一章（略）

第二章 MOS器件物理基础

1. MOSFET 的结构（以NMOS为例）

注：n区得保持与 P 型衬底反偏，防止器件漏电、不以预期目的工作。

2. MOS管的 I-V 特性

2.1 电流方程

对于 NMOS 管，

处于三极管区（线性区）时有电流方程：
$I_{D}=\mu_{n} C_{\mathrm{ox}} \frac{W}{L}\left[\left(V_{G S}-V_{T H}\right) V_{D S}-\frac{1}{2} V_{D S}^{2}\right]$
处于饱和区时有电流方程：
$I_D=\frac{1}{2}\mu _nC_{\mathrm{ox}}\frac{W}{L'}\left( V_{GS}-V_{TH} \right) ^2$
NMOS 管符号：

2.2 I_D 与 V_DS 之间的关系

分析：

V_DS < 过驱动电压 $V_{G S}-V_{T H}$ 时, 器件进入三极管区, 沟道导通
V_DS > 过驱动电压 $V_{G S}-V_{T H}$ 时, 器件进入饱和区, 沟道夹断（夹断是我们想要的性质！）
V_DS << 过驱动电压 $V_{G S}-V_{T H}$ 时, 器件进入深三极管区，有导通电阻：
$R_{\mathrm{on}}=\frac{1}{\mu_{\mathrm{n}} C_{\mathrm{ox}} \frac{W}{L}\left(V_{\mathrm{GS}}-V_{\mathrm{TH}}\right)}$
此时的MOS管工作状态如下：

2.3 跨导 g_m

饱和区跨导公式：

$\begin{aligned} g_{\mathrm{m}}=\left. \frac{\partial I_{\mathrm{D}}}{\partial V_{\mathrm{GS}}} \right|_{V_{\mathrm{DS}, \mathrm{cons}}}&=\mu _{\mathrm{n}}C_{\mathrm{ox}}\frac{W}{L}\left( V_{\mathrm{GS}}-V_{\mathrm{TH}} \right) \\ &=\sqrt{2\mu _{\mathrm{n}}C_{\mathrm{ox}}\frac{W}{L}I_{\mathrm{D}}} \ \ \ \ \left( \text{用}I_D\text{替代（}V_{GS}-V_{TH}\text{）} \right) \\ &=\frac{2I_{\mathrm{D}}}{V_{\mathrm{GS}}-V_{\mathrm{TH}}} \ \ \ \ \left( \text{用}I_D\text{替代（}\mu _nC_{ox}\text{）} \right)\\ \end{aligned}$

三极管区跨导公式：

$\begin{aligned} g_{\mathrm{m}} &=\frac{\partial}{\partial V_{\mathrm{GS}}}\left\{\frac{1}{2} \mu_{\mathrm{n}} C_{\mathrm{ox}} \frac{W}{L}\left[2\left(V_{\mathrm{GS}}-V_{\mathrm{TH}}\right) V_{\mathrm{DS}}-V_{\mathrm{DS}}^{2}\right]\right\} \\ &=\mu_{\mathrm{n}} C_{\mathrm{ox}} \frac{W}{L} V_{\mathrm{DS}} \end{aligned}$
（跨导与V_DS 有关，V_DS 为输出，最好与 g_m 无关，且最小）

3. 二级效应

3.1 体效应

目的是利用体效应减小V_TH ：做成深n阱避免当V_SB 变小⬇️ 时，S 极PN结导通

考虑体效应后的阈值电压： $V_{\mathrm{TH}}=V_{\mathrm{TH} 0}+\gamma\left(\sqrt{\left|2 \Phi_{\mathrm{F}}+V_{\mathrm{SB}}\right|}-\sqrt{\left|2 \Phi_{\mathrm{F}}\right|}\right)$

影响阈值电压的两个因素：

衬底电压 $V_{B}$ 变得更负(NMOS), 耗尽层电荷总数 $Q_{d e p}(Q_ d)$ 增加,阈值电压 $V_{TH}$ 增大
$V_{\mathrm{TH}}=\Phi_{\mathrm{MS}}+2 \Phi_{\mathrm{F}}+\frac{Q_{\mathrm{dep}}}{C_{\mathrm{ox}}}$
源极-衬底电压 $V_{SB}$ 发生改变 (源极电压相对衬底电压改变)，影响阈值电压 $V_{TH}$
$V_{\mathrm{TH}}=V_{\mathrm{TH}0}+\gamma \left( \sqrt{\left| 2\Phi _{\mathrm{F}}+V_{\mathrm{SB}} \right|}-\sqrt{\left| 2\Phi _{\mathrm{F}} \right|} \right)$

3.2 沟道长度调制效应

考虑沟道长度调制效应后的漏电流 (饱和区)
考虑沟道长度调制效应后的 $I_D - V_{DS}$ 曲线： $I_{\mathrm{D}}\approx \frac{1}{2}\mu _{\mathrm{n}}C_{\mathrm{oz}}\frac{W}{L}\left( V_{G\mathrm{S}}-V_{\mathrm{TH}} \right) ^2\left( 1+\lambda V_{DS} \right)$ ，（ $\lambda$ 为沟道长度调制系数）（ $\lambda \propto \frac{1}{L}$ ）(实线部分、斜率升高)

考虑沟道长度调制效应后的跨导 g_m
$\begin{aligned} g_{\mathrm{m}}&=\mu _{\mathrm{n}}C_{\mathrm{ox}}\frac{W}{L}\left( \left( V_{\mathrm{GS}}-V_{\mathrm{TH}} \right) \left( 1+\lambda V_{DS} \right) \right.\\ &=\sqrt{2\mu _{\mathrm{n}}C_{OX}(W/L)I_{\mathrm{D}}\left( 1+\lambda V_{\mathrm{ns}} \right)}\\ &=\frac{2I_{\mathrm{D}}}{V_{\mathrm{GS}}-V_{\mathrm{TH}}}\\ \end{aligned}$

3.3 亚阈值导电性

（当V_GS < V_TH，I_D 并非无限小，而是与 V_GS 表现为指数关系）该性质用于低功耗和低频电路，电流小
$I_{\mathrm{t}}=I_0\exp \frac{V_{GS}}{\zeta V_T}\quad$

亚阈值效应会导致按比例缩小理论（在 0.13um 及之后的工艺中）失效, 因为依据比例缩小理论使得阈值电压减小, 在大规模电路中的亚阈值效应使得漏电太大。

（V_TH = 240mV 时，V_GS = 0 （关断）时 I_D 为导通的 $\frac{1}{1000}$ ，当拥有一亿个器件会消耗较大的电流）

第三章单级放大器

1. 共源级

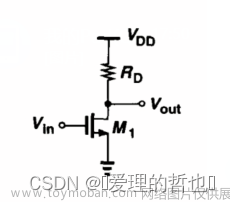
1.1 采用电阻做负载的共源极

电路图
V_out - V_in 曲线以及大信号分析
小信号分析及增益（管子要求必须在饱和区，因为在线性区跨导下降**【例2.3】**）

$A_V = -g_m R_D$

$V_{out}/V_{in}=-g_m\left( r_o \parallel R_D \right)$

跨导随输入电压变化草图

饱和区部分的跨导公式为： $g_m=\mu _nC_{ox}\frac{W}{L}\left( V_{in}-V_{TH} \right)$

线性区部分的跨导公式为： $g_m=\mu _nC_{ox}\frac{W}{L}V_{DS}$ ，（V_in ⬆️，I_D⬆️ ，R_D 分压⬆️，V_DS ⬇️ ）

在线性区跨导缺点：与输出电压有关且大小减小

1.2 采用二极管连接性器件作负载的共源级

以用 PMOS 器件作二极管连接性负载的共源级

$\left| V_{GS2}-V_{TH2} \right|=\left| V_{OUT}-V_{DD}-V_{TH2} \right|<\left| V_{DS2} \right|=\left| V_{OUT}-V_{DD} \right|$

M₂ 一直保持在饱和区

NMOS 作负载存在偏衬效应，改善方法：换成PMOS或者使用深阱工艺
大信号分析：
- 当V_in < V_TH，M₁ 截止，M₂ 处于饱和区，用 M₂ 饱和区 I_D 公式来看：
  $I_D=\frac{1}{2}\mu _nC_{\mathrm{ox}}\frac{W}{L'}\left( V_{GS}-V_{TH} \right) ^2$
  
  $V_{\text {GS2 }}-V_{T H 2}=0, \quad V_{\text {out }}=V_{D D}-\left|V_{T H 2}\right|$
- 当V_in < V_TH，M₁ 饱和，进行一些等式代换有： $\frac{\left|V_{\mathrm{GS} 2}-V_{\mathrm{TH} 2}\right|}{V_{\mathrm{GS} 1}-V_{\mathrm{TH} 1}} \approx A_{\mathrm{v}}$
- 当V_in > V_OUT + V_TH，M₁ 进行线性区
- 图示：
  
  (NMOS 为负载时的 $V_{OUT} - V_{in}$ 关系，可供参考)
小信号分析：

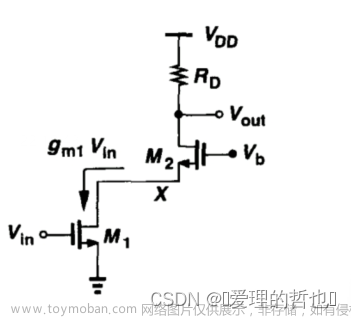
1.3 采用电流源作负载的共源级

电流源作负载的共源级
- 小信号分析
红色部分可看成以下部分：

增益：$A_V=-g_m\left( r_{o1}\parallel r_{o2} \right) $
- 大信号分析（V_OUT 取值范围）
条件: Vout 取值需使得 $M_{1}$ 和 $M_{2}$ 均在饱和区工作

对于 $M_{1} $，
$V_{G S 1}-V_{T H 1}\le V_{D S 1} \Rightarrow \mathrm{V}_{\text {in }}-\mathrm{V}_{\text {TH } 1}\le\mathrm{V}_{\text {out }}$

对于 $M_2$ ，
$\left| V_{GS2}-V_{TH2} \right|\le \left| V_{DS2} \right| \\ \begin{aligned} &\Rightarrow \left| V_{\mathrm{GS}2}-V_{TH2} \right|\le V_{DD}-V_{\mathrm{out}}\\ &\Rightarrow V_{\mathrm{out}}\le V_{DD}-\left| V_{\mathrm{GS}2}-V_{TH2} \right|\\ \end{aligned}$

1.4 有源负载的共源级（CMOS反相器）

$A_V=-\left( g_{m1}+g_{m2} \right) \left( r_{o1}\parallel r_{o2} \right)$

1.5 工作在线性区的MOS为负载的共源级

1.5 带源级负反馈的共源级

小信号分析

$\text { 定义电路的等效跨导 } G_{m}=\partial l_{D} / \partial V_{i n}, M_{1} \text { 跨导 } g_{m}=\partial l_{D} / \partial V_{G S}$ 。
$G_{\mathrm{m}}=\frac{g_{\mathrm{m}}}{1+g_{\mathrm{m}}R_{\mathrm{s}}}\quad A_V=-G_{\mathrm{m}}R_D=-\frac{\left( R_{\mathrm{D}} \right)}{\frac{1}{\frac{1}{g_{\mathrm{m}}}+R_{\mathrm{s}}}}\text{（分子为漏极点电阻，分母为源极通路）}$

源极通路可以表示如下：
大信号分析

$R s = 0$ 时, I_D 和 g_m 变化如下：

$\neq 0$ 时, I_D 和 g_m 变化如下：

分析：

I_D 较小时, $g_m$ 也小, 1/g_m $>$ R_s , 根据G_m的表达式, $G_m=g_m$ ; 随着过驱动电压持续增大, g_m增大, $G_m=1 / R_s$ , 即 $I_D / V_{i n}=1 / R_s$ (线性关系)

2. 源跟随器

电路图
大信号分析

输出电压V_out随输入电压V_in变化，且两者之差为 V_GS
小信号分析

$A_{V}=\frac{g_{\mathrm{m}} R_{\mathrm{s}}}{1+\left(g_{\mathrm{m}}+g_{\mathrm{mb}}\right) R_{\mathrm{s}}}$

电压增益与输入电压关系
分析：

当 V_in 约等于 V_th 时，g_m 开始增大，增益 A_v 接近等于 $\frac{g_m}{g_m+g_{mb}}$ （即忽略1/ R_s）A_v= 1/(1+n)，随着 V_out 增大，n也缓慢减小，A_v 趋近于1)
源跟随器驱动有限负载（考虑沟道长度调制效应和体效应）

电路图及小信号分析：

小信号电路图继续化简：

$A_{v}=\frac{R_{\mathrm{eq}}}{R_{\mathrm{eq}}+\frac{1}{g_{m}}}$

3. 共栅级

3.1 基本电路

小信号分析

忽略沟道长度调制效应，有 $\frac{\partial V_{out\,\,}}{\partial V_{in}}=g_{\mathrm{m}}(1+\eta )R_{\mathrm{D}}$
大信号分析

分析：

假设 V_in 从某一个大的正值开始减小。当 $V_{in}\geqslant V_b-V_{TH}$ 时，M₁ 处于截止区，V_out=V_DD；V_in 小一点 _M1 进入饱和区，当 V_in 减小时，V_out 也随之减小(由 I_D 公式得到)，当 V_out 小到一定时 M₁ 进入线性区。

3.2 输出电阻为有限值的共栅级

$\frac{V_{\mathrm{aut}}}{V_{\mathrm{in}}}=\frac{\left( g_{\mathrm{m}}+g_{mb} \right) r_o+1}{r_o+\left( g_{\mathrm{m}}+g_{\mathrm{mb}} \right) r_oR_{\mathrm{S}}+R_{\mathrm{S}}+R_{\mathrm{D}}}R_{\mathrm{D}}$

3.3 共源共栅级（Cascode）

基本电路
- 偏置条件（M₁ 和 M₂ 工作在饱和区）
  $V_{\mathrm{out}}\geqslant \left( V_{GS}-V_{\mathrm{th}1} \right) +\left( V_{GS2}-V_{\mathrm{th}2} \right) \,\,(\text{两个过驱动电压之和)}$
- 大信号分析
  
  分析：
  
  (M₂ 有反型层但是无电流)，V_out= V_DD，V_X= V_b - V_th2 (如果 M₂ 导通进入饱和区，用饱和区 I_D 公式得到)：当 V_in > V_th1，M₁ M₂ 饱和，I_D 增大，V_out 下降；因为 I_D 增大，V_GS2 也增大，所以 V_x 减小；V_in 继续增大，出现 M₁ 进入线性区和 M₂ 进入饱和区的结果不确定。
- 输出阻抗
  
  $R_{\mathrm{bu}1}=\underbrace{\left[ 1+\left( g_{\mathrm{m}2}+g_{\mathrm{mb}2} \right) r_{02} \right] r_{01}}+r_{02} \\ (\text{将}M_1\text{的阻抗提高到原来的(}g_{m2}+g_{mb2})r_{o2}\text{倍)}$
- 屏蔽效应
  
  输出节点电压变化对共源共栅器件CG级源级的电压变化很小

3.4 折叠式共源共栅级

特点：设计思路和共源共栅一样，共源输入共栅输出，区别在于输入输出器件不一定是同一类型

电路图
大信号分析

分析：

（假设输入电压由V_DD减小到0）文章来源地址https://www.toymoban.com/news/detail-741488.html
- 如果 $V_{in}>V_{DD}-\left| V_{TH1} \right|$ 时，M₁ 截止，M₂ 饱和（I₁ 不太大的情况下，太大进入线性区）, $V_{out}=V_{DD}-I_D\times R_D$ ；
- V_in 继续减小，M₁ 进入饱和区（I_D2 较大，所以由饱和电流公式得 V_x 较小），I_D1 增大，l_D2 减小，当 I_D1 = l₁ 时，I_D2 =0，这时有 $V_b-V_{TH2}= V_x$ 且 V_in= V_in1；
- 当 V_in 继续减小，l_D1 趋向于等于l₁ ，所以M₁ 得进入线性区使得 l_D1 = l₁.

到了这里，关于模拟集成电路笔记 | 第一部分 | Chapter 1-3的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！

模拟集成电路笔记 | 第一部分 | Chapter 1-3